整数的唯一分解定理
整除性


例题





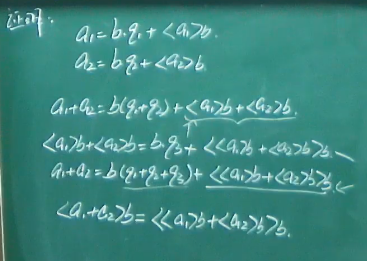
例题

最大公因数


例题
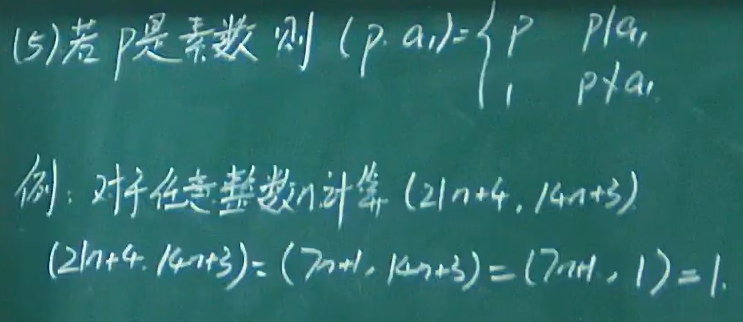
- 例题用到上面性质4


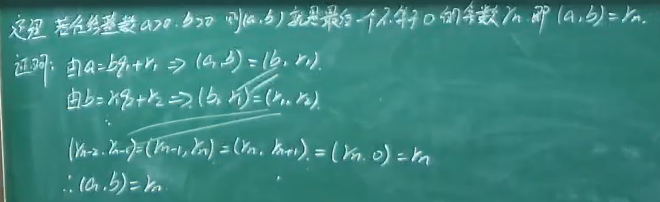

- 下面证明会用到该定理


例题








最小公倍数




整数的唯一分解定理



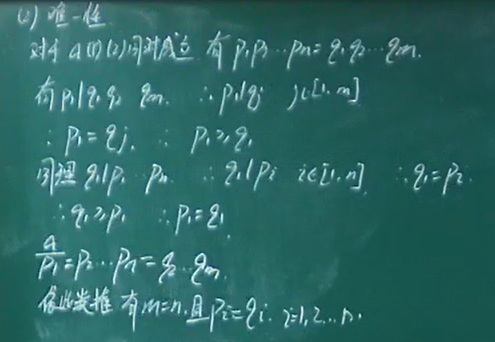
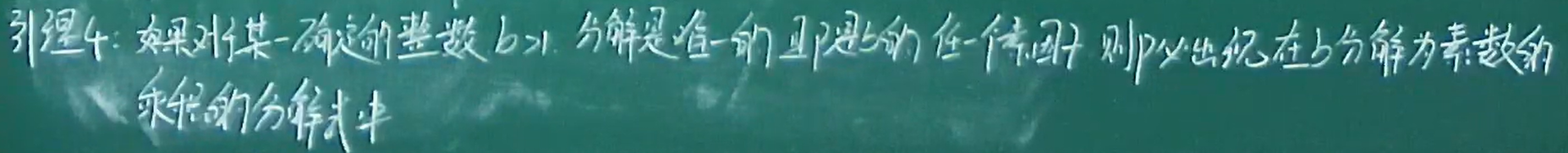







- 下面例题会用到

例题


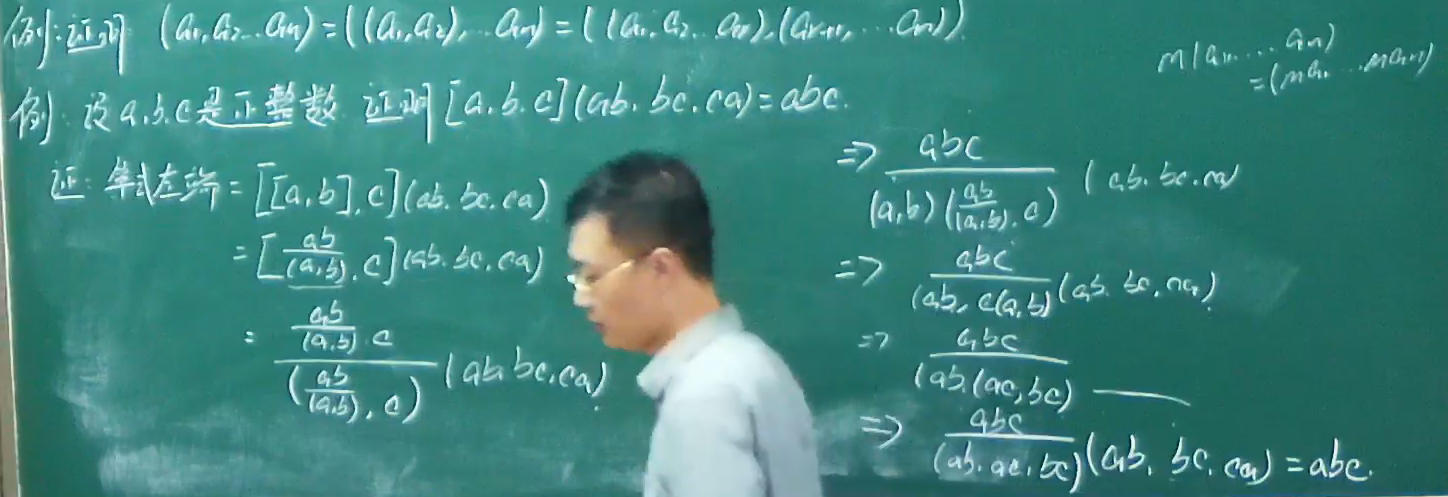
同余式
同余的定义和基本性质






例题

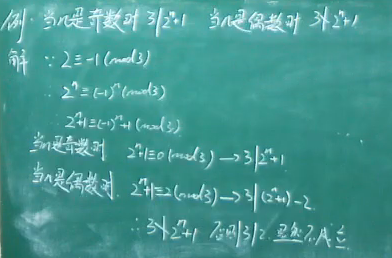



剩余类和完全剩余系







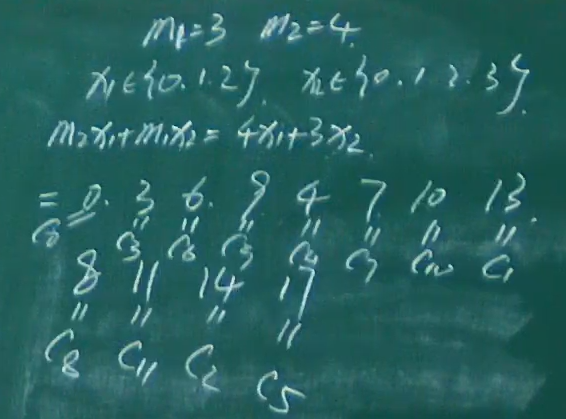

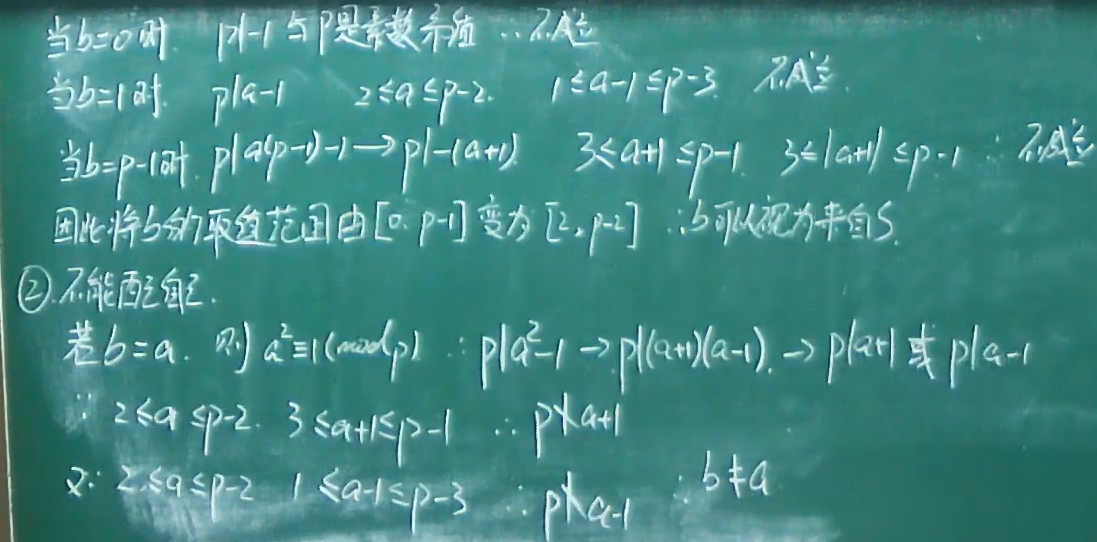

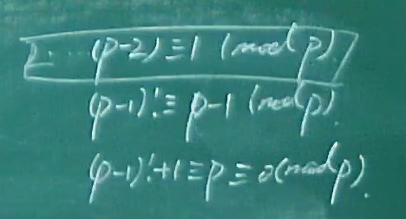
- 定理变式
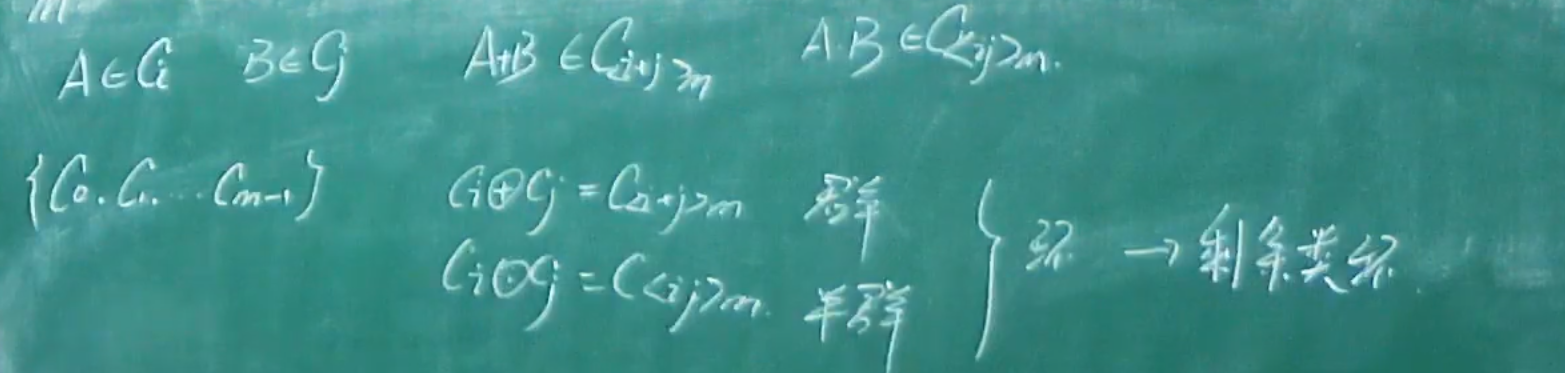

例题



缩系


- 上面缩系定义中,“显然”的原因






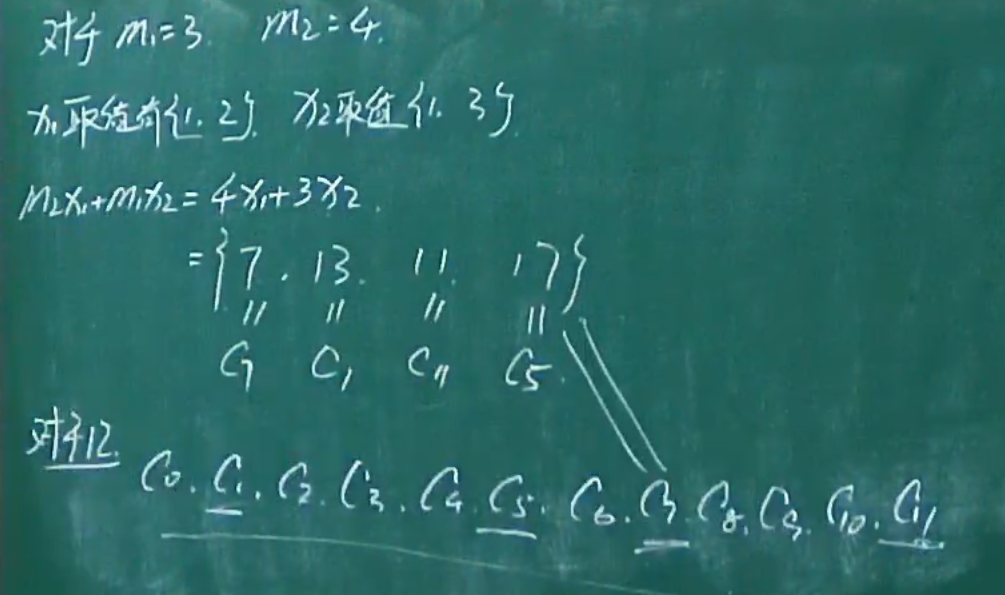



- 右边是另一种不严谨的证法
例题


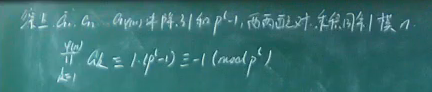
一次同余式

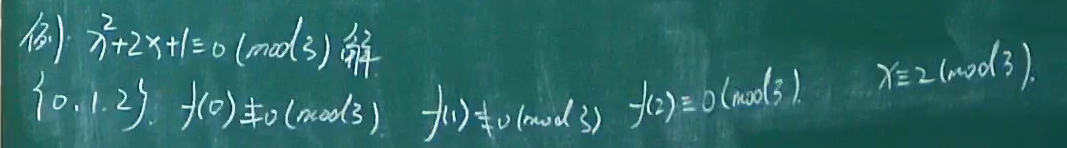



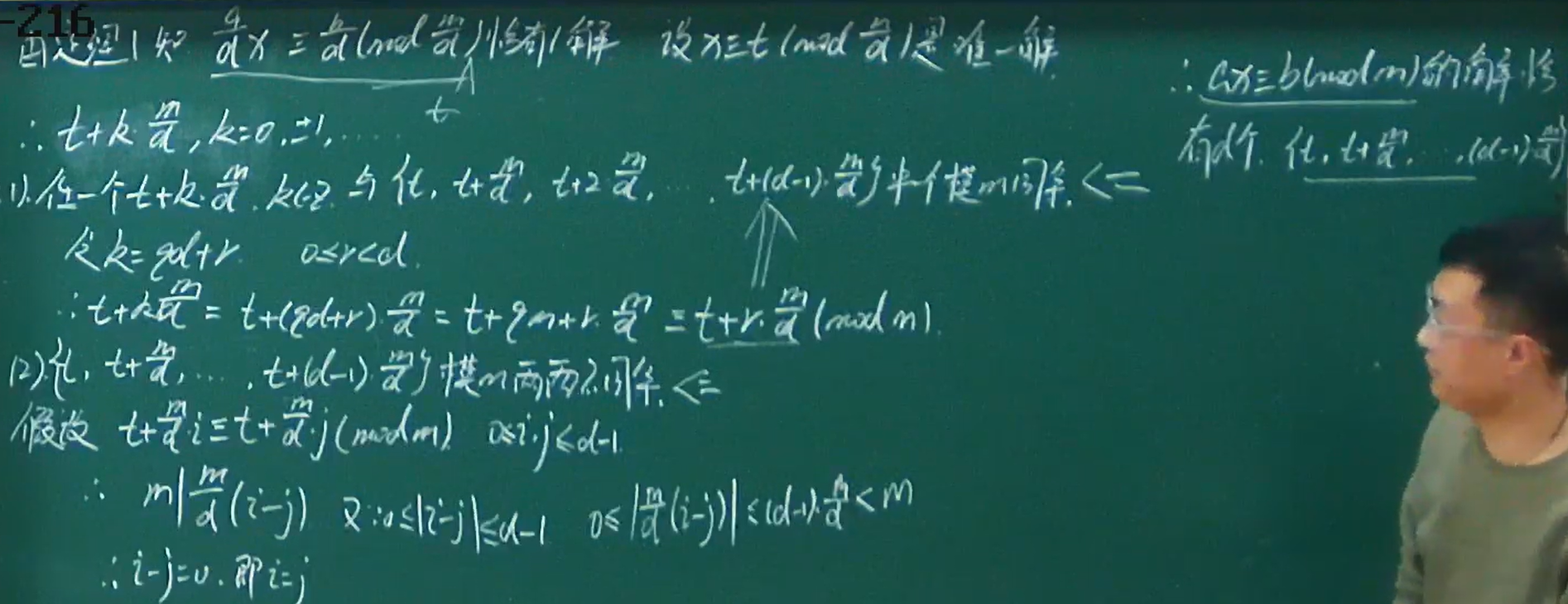
例题



- xk=yk/a

- 方法(2)是定理2


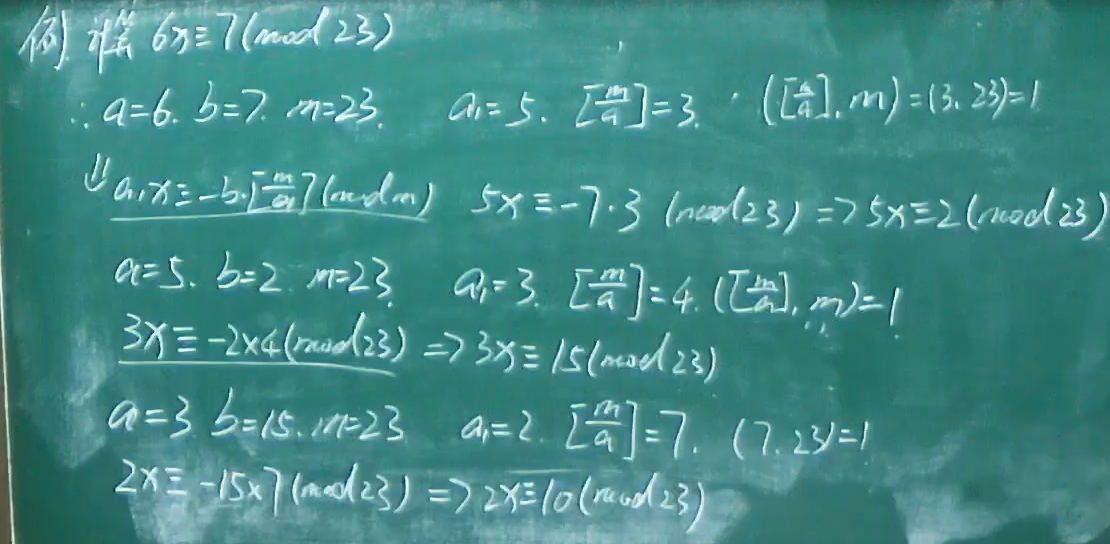
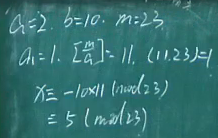
模数是素数的同余式

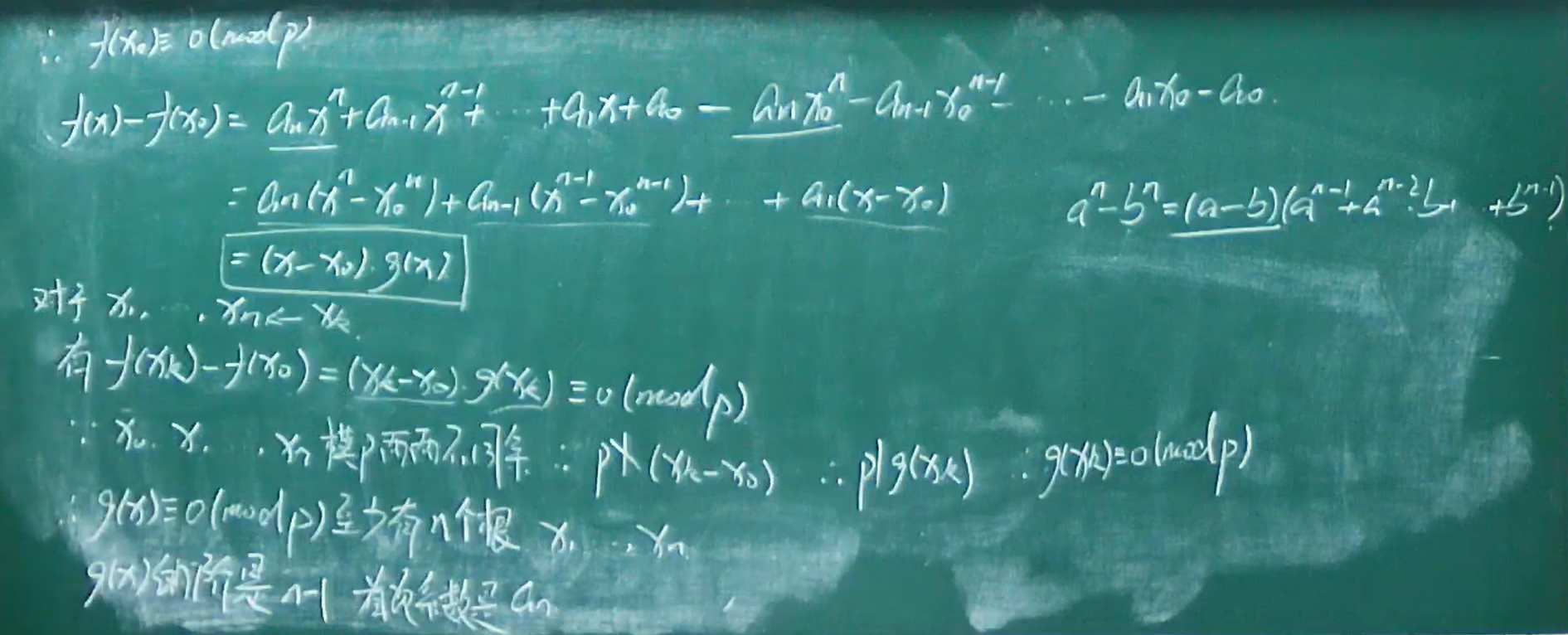


孙子剩余定理


例题




例题



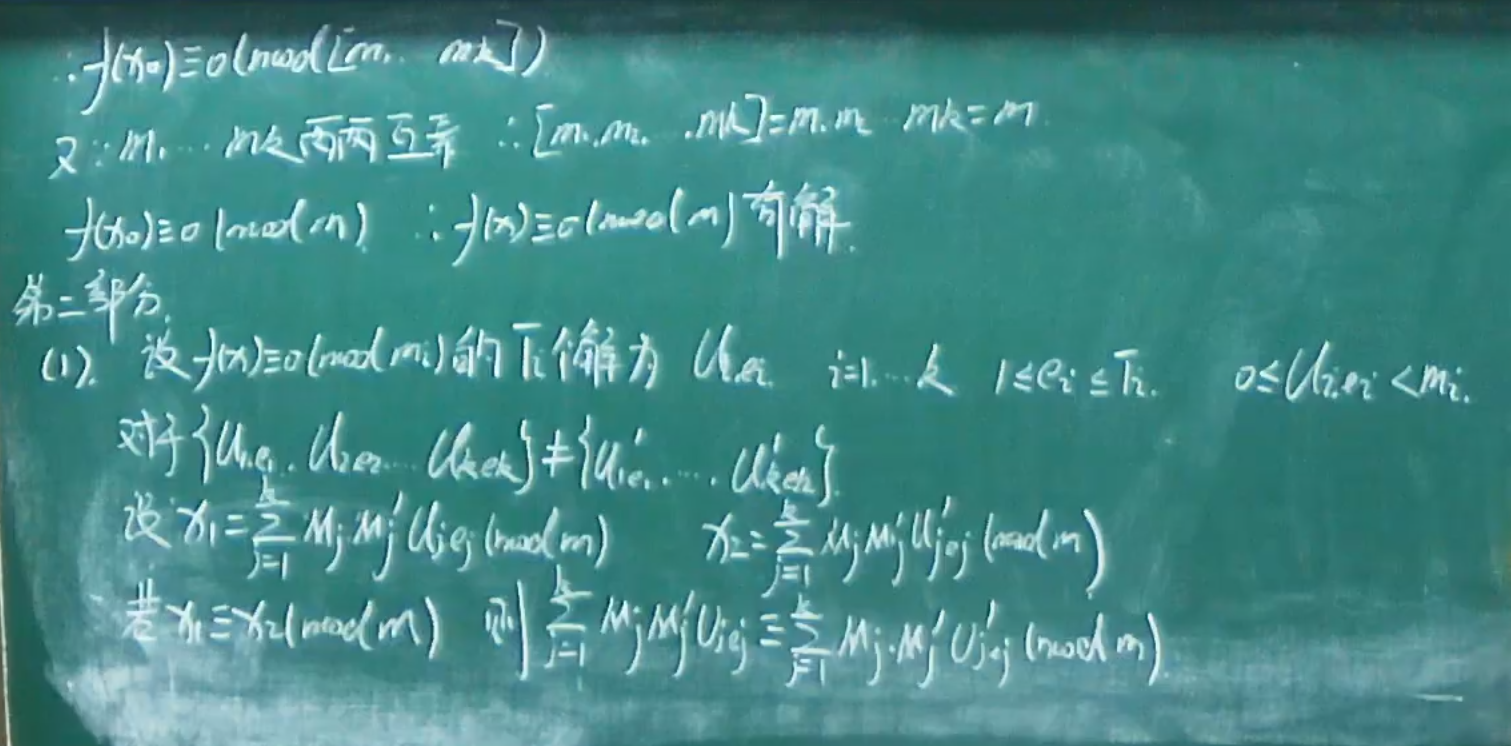



例题
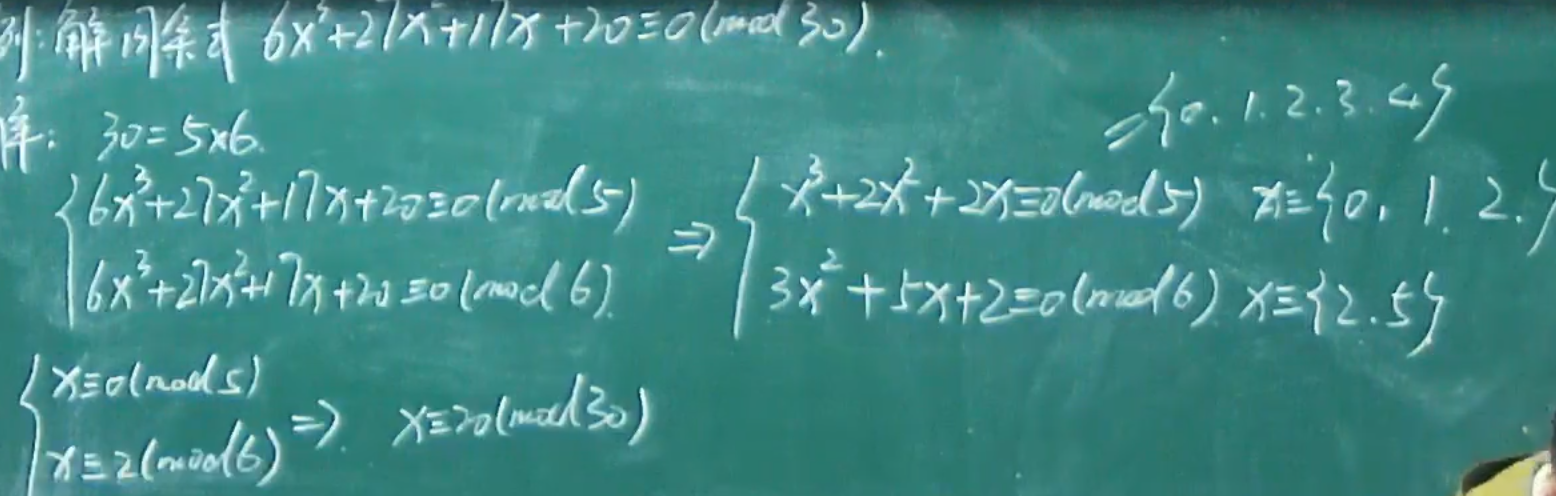

模数是素数幂的同余式



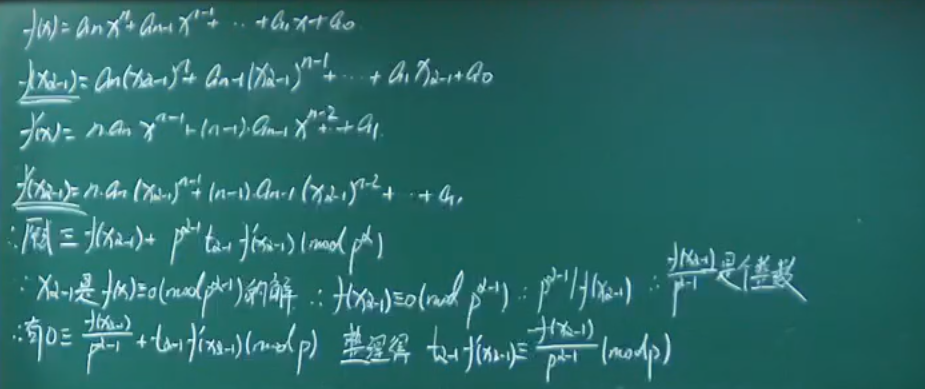
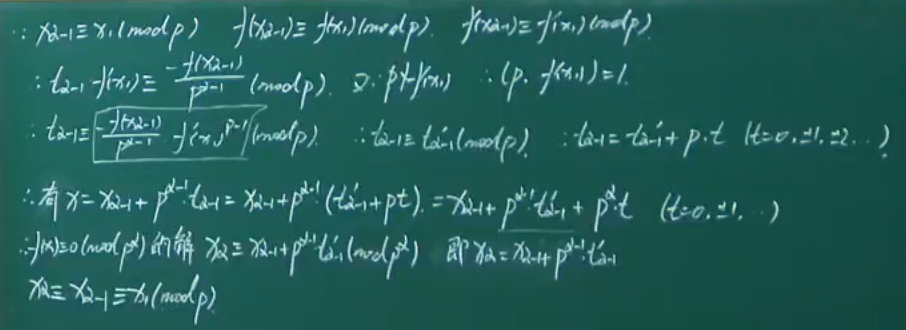
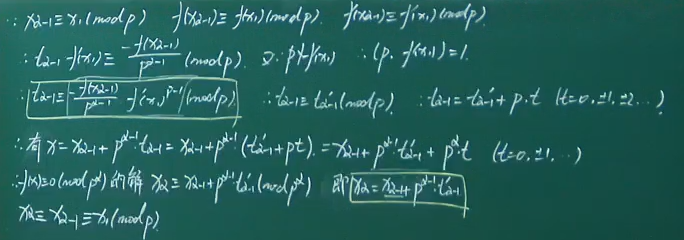


例题



回顾


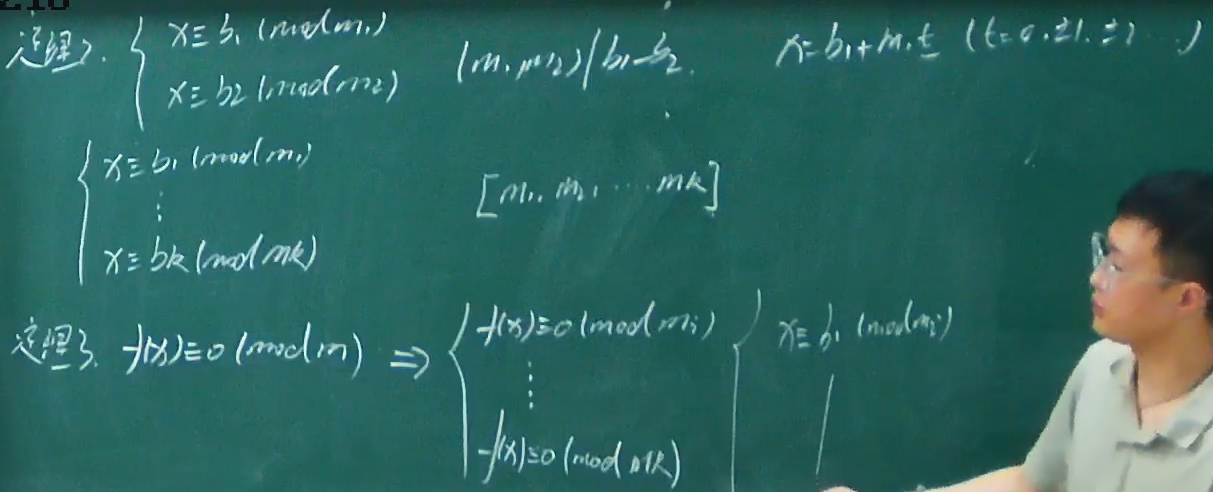

整数的剩余表示


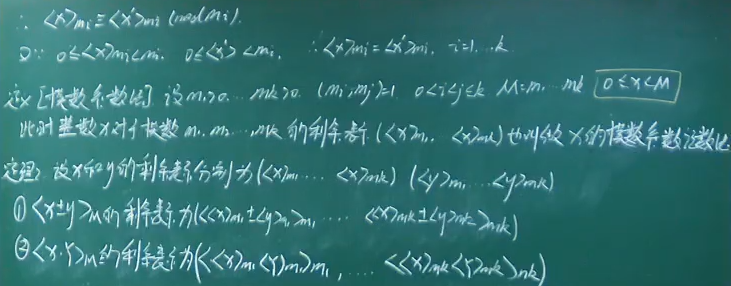
例题

数论函数
数论函数pot

‖是恰好整除- n中有m个p
例题

{}表示小数部分

例题






例题

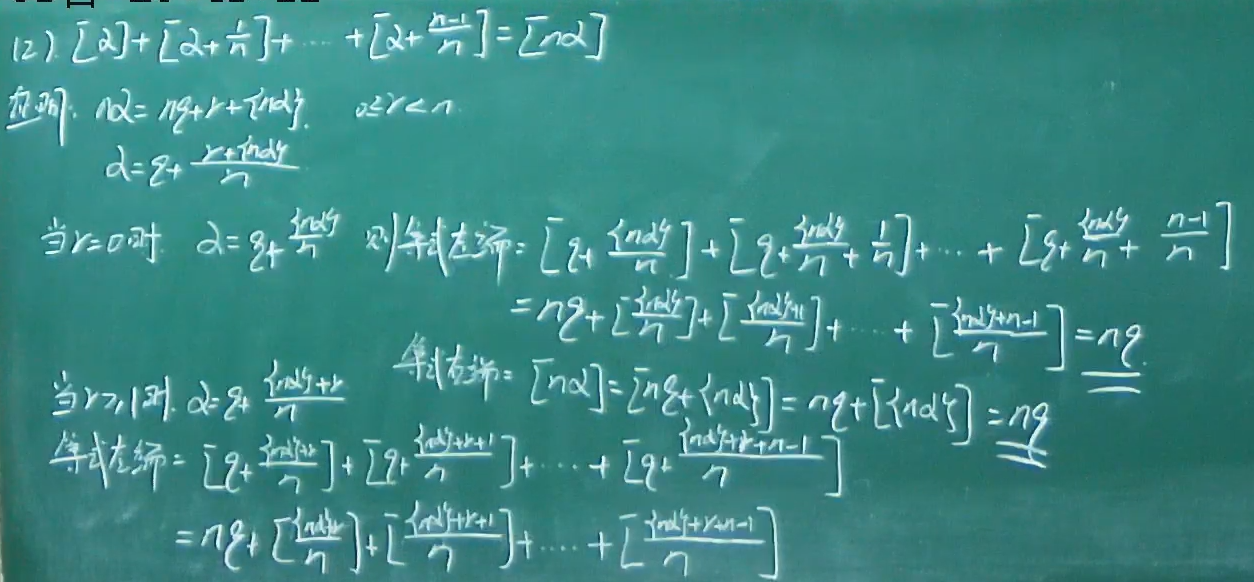

麦比乌斯函数

- $-1^s$:s是素数的个数

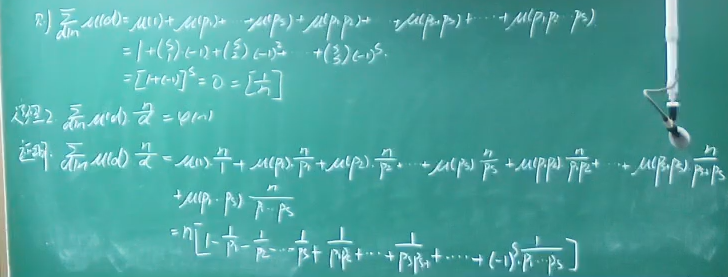
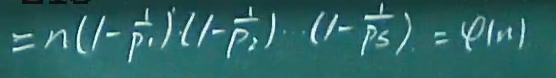

欧拉函数

- d|n:d整除n
- d跑遍n的所有因子,所有因子的欧拉函数和=n
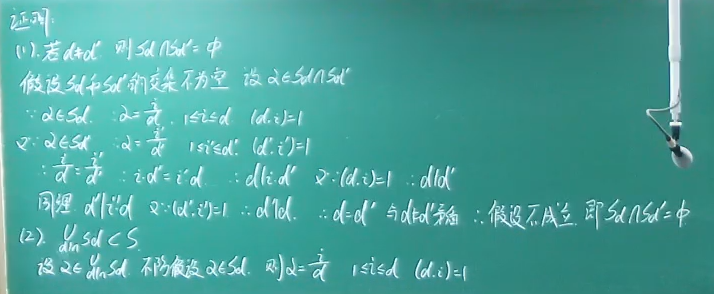



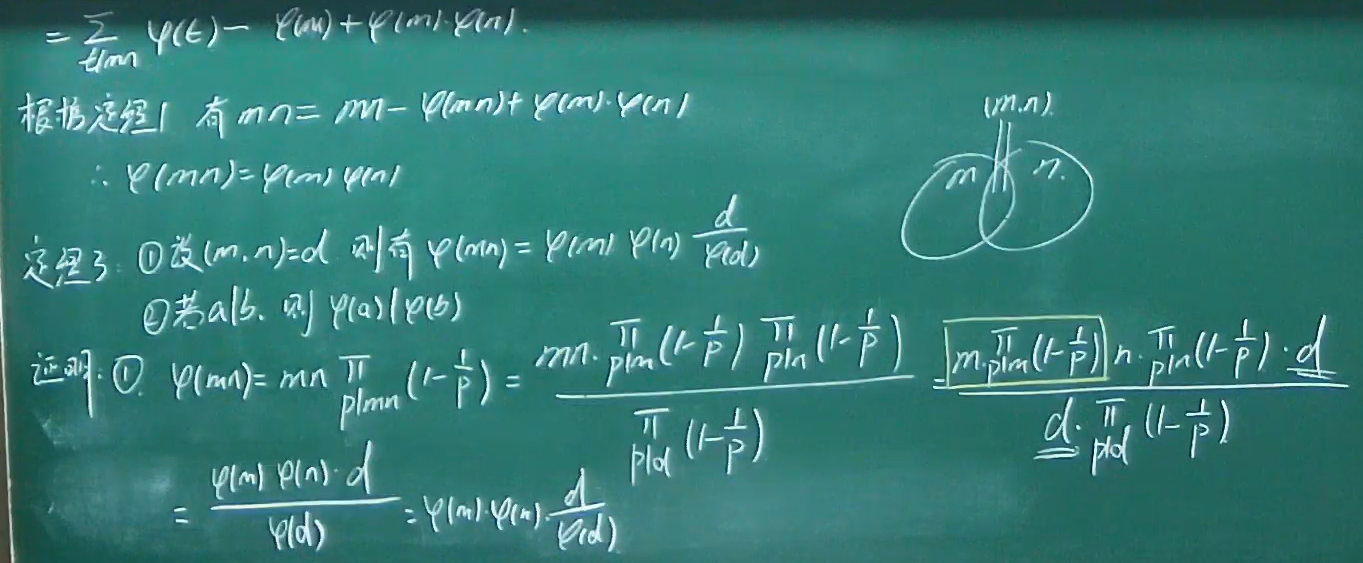
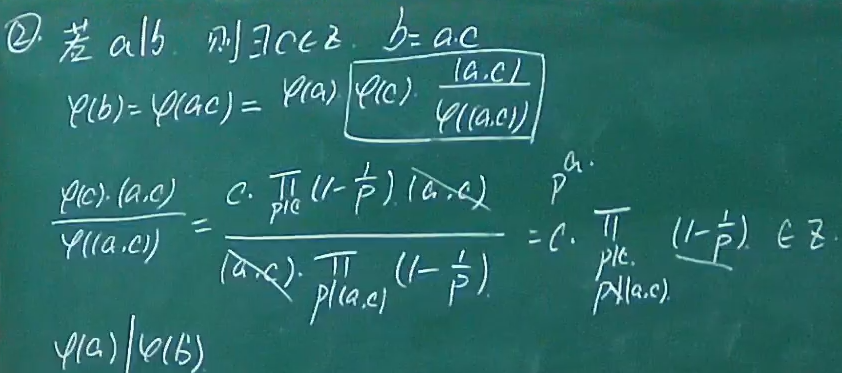
数论函数的狄利克雷乘积


- 定义说明封闭性
- 定理一说明交换律、结合律
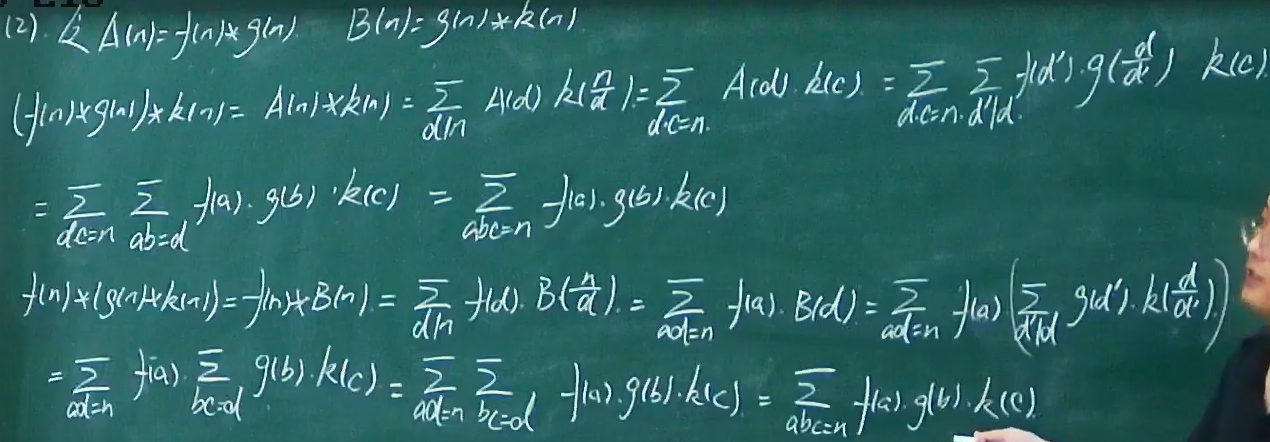

- 定理二说明单位元
- 定理三说明逆元
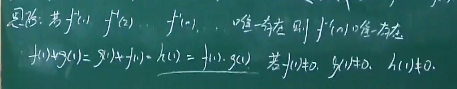

麦比乌斯反演公式

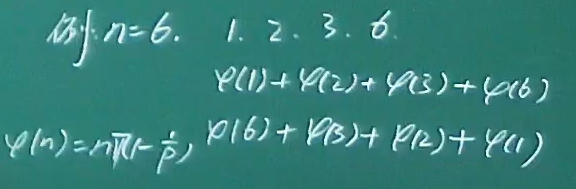
- 欧拉例
- 麦的公式

- 麦的公式

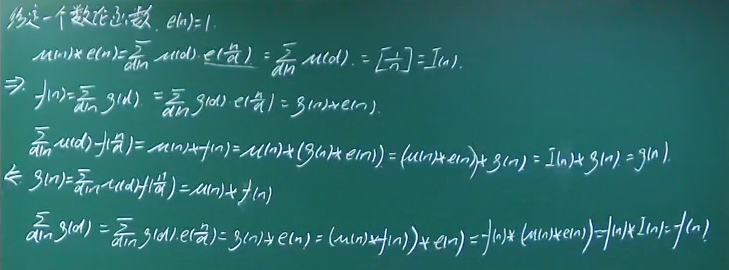
例题
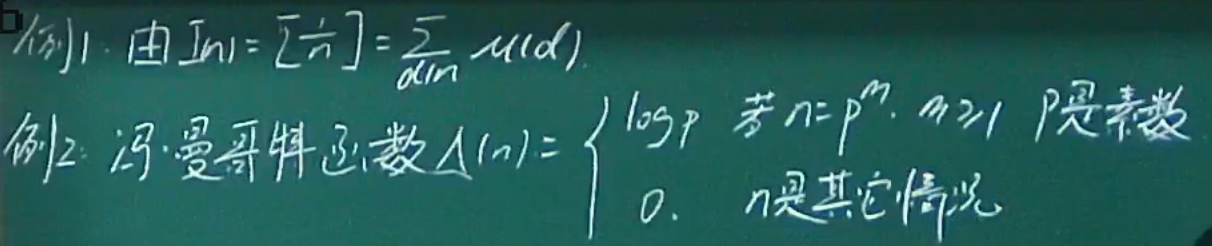


积性函数

- 去掉互素条件就是完全积性
- 4圈起来后面定理用到


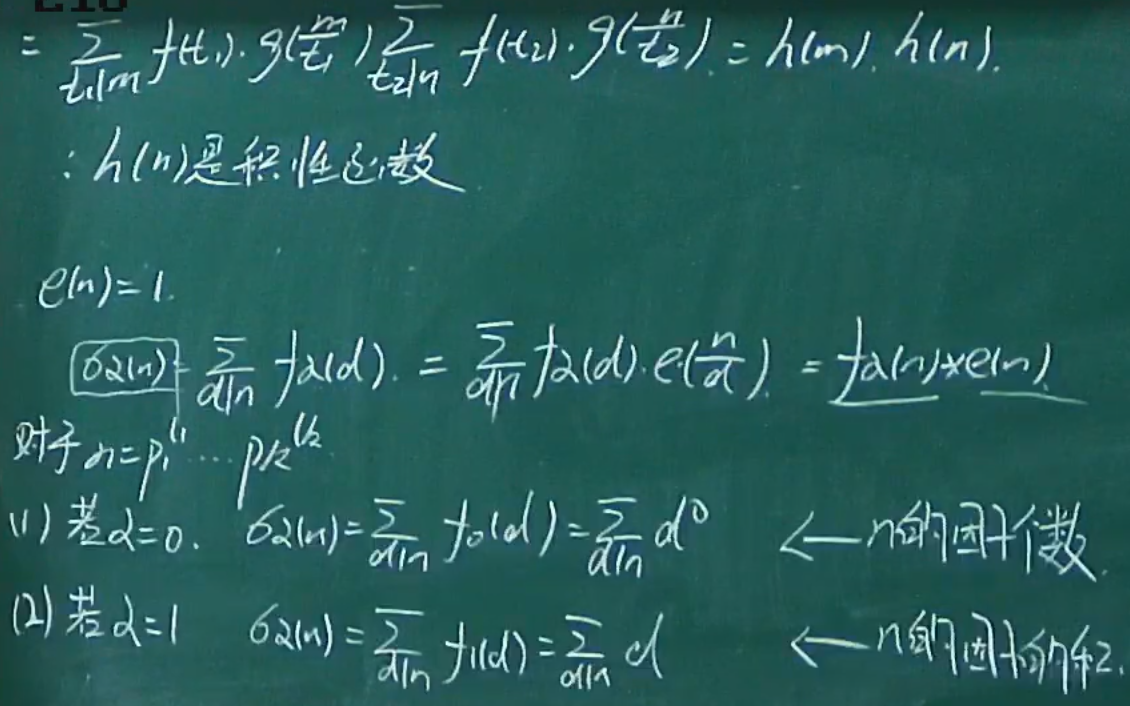
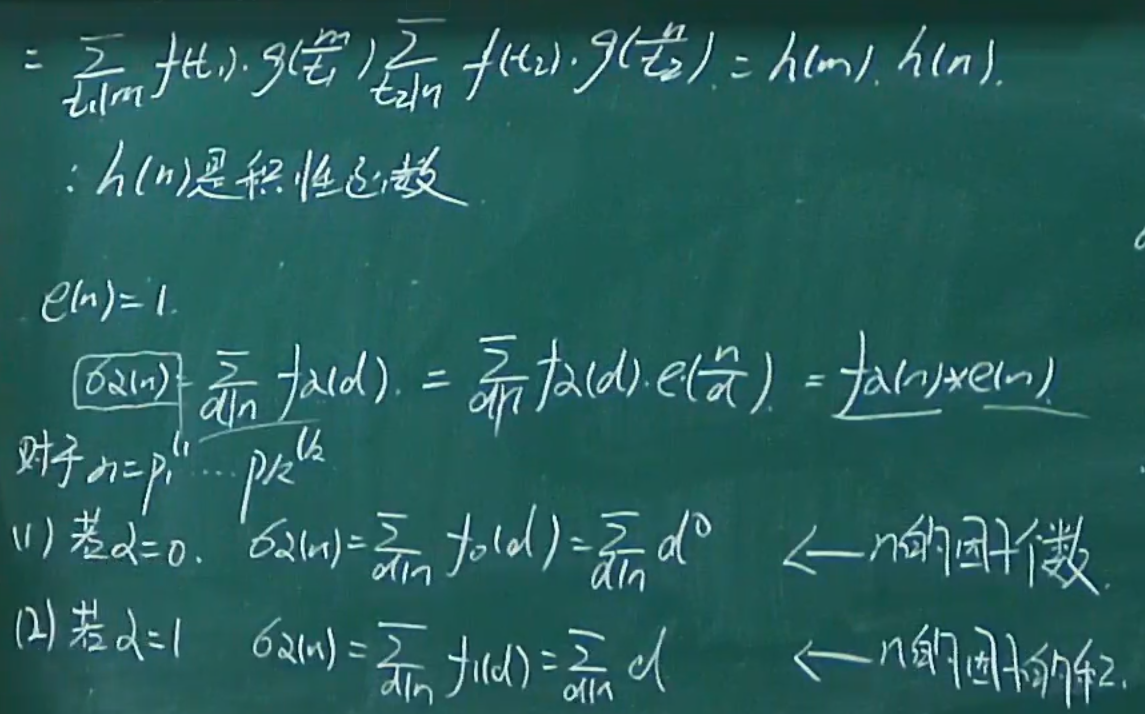
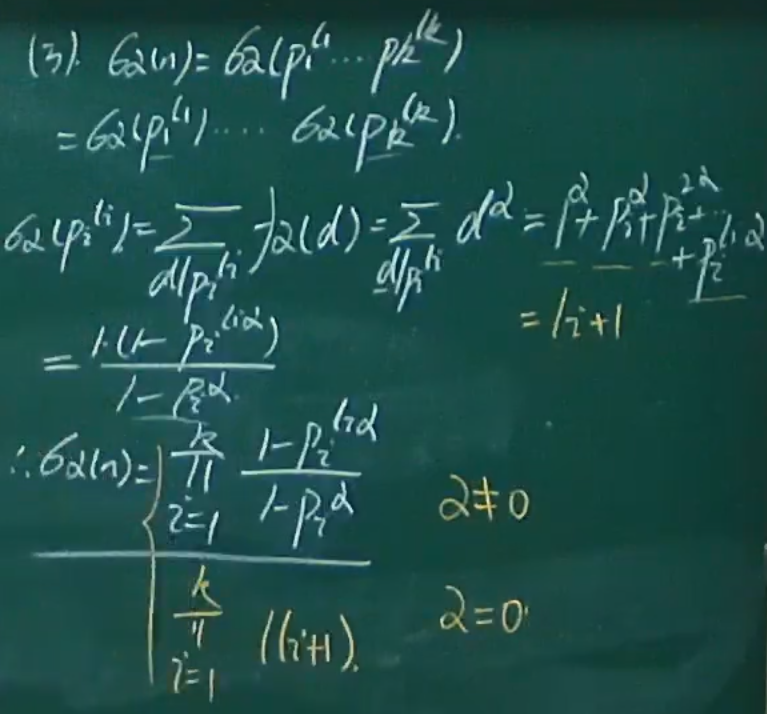

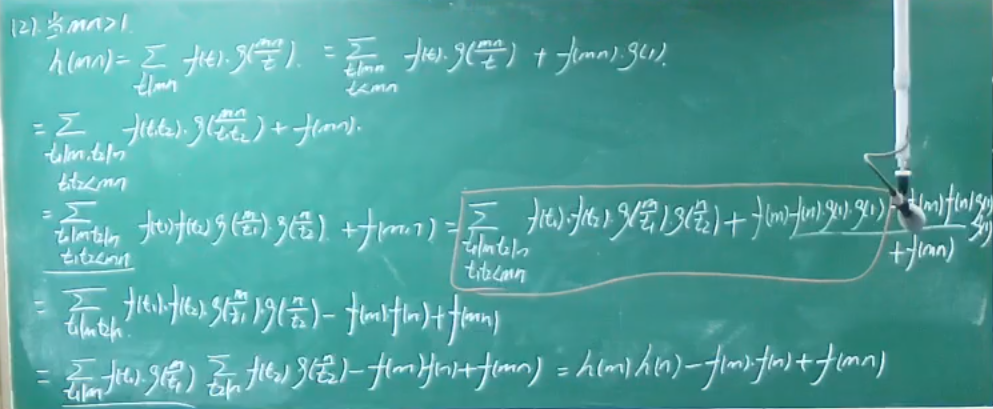


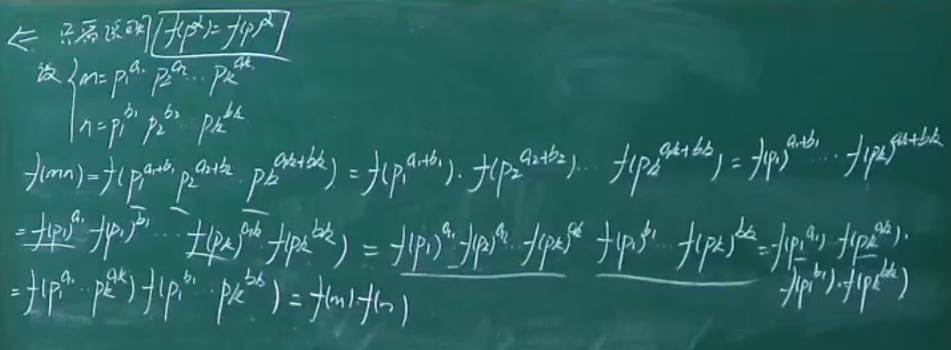
二次剩余
二次剩余


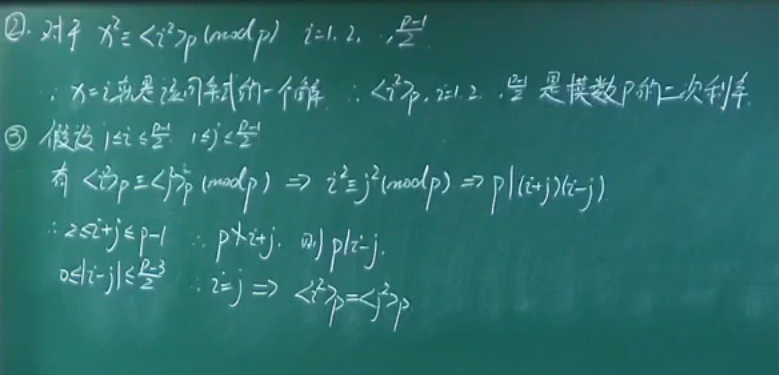


勒让德符号






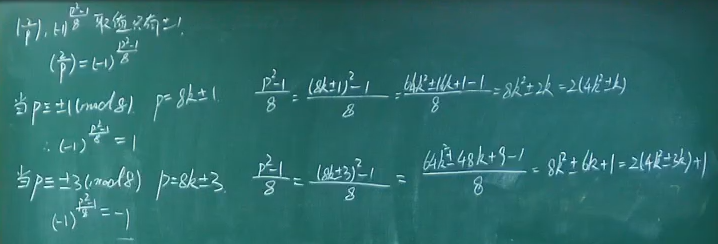
例题

高斯引理

- n对p的剩余、n/2对p的剩余、……、(p-1)/2对p剩余,共(p-1)/2个数
- n对p的勒让德符号值=$(-1)^m$


例题









二次互反律

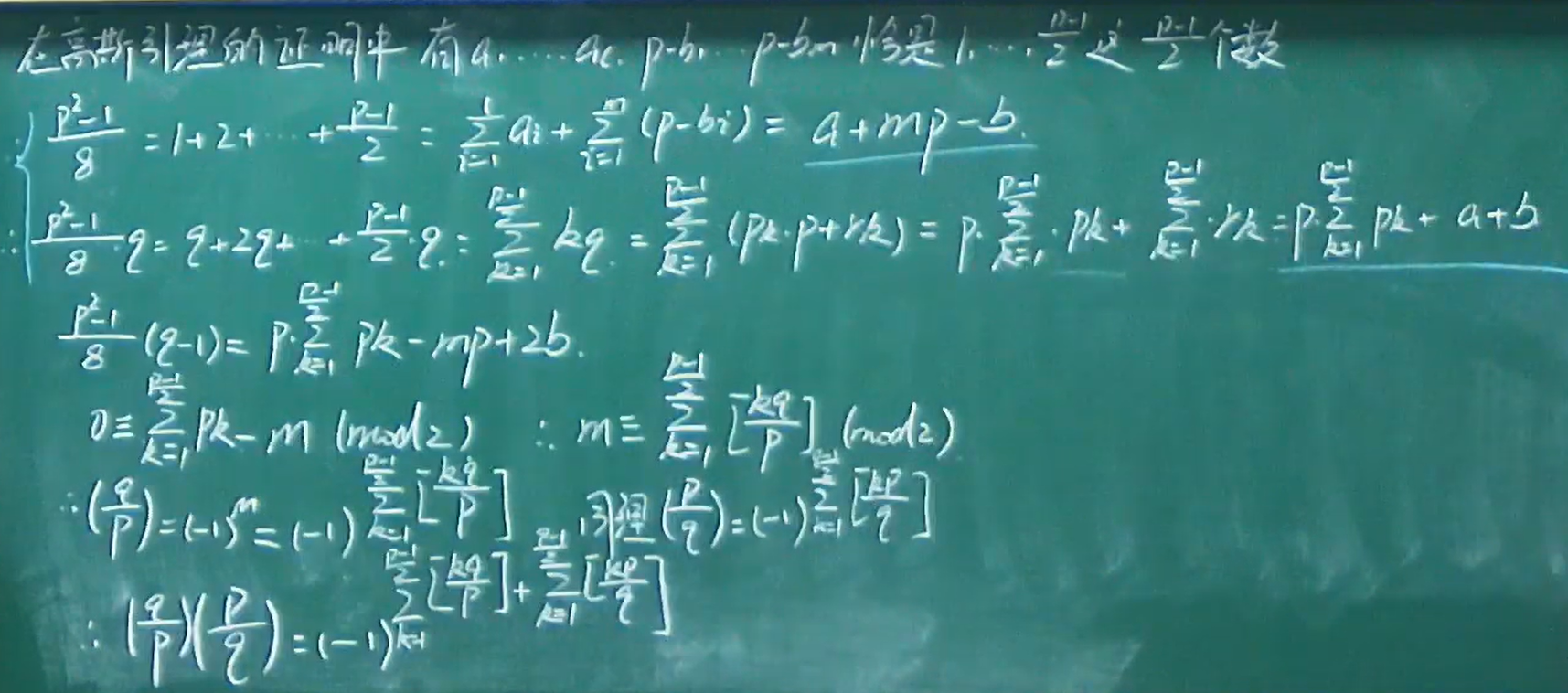


例题

二次同余式的解法和解数

- (n/p)=1:n对p的勒让德符号为1
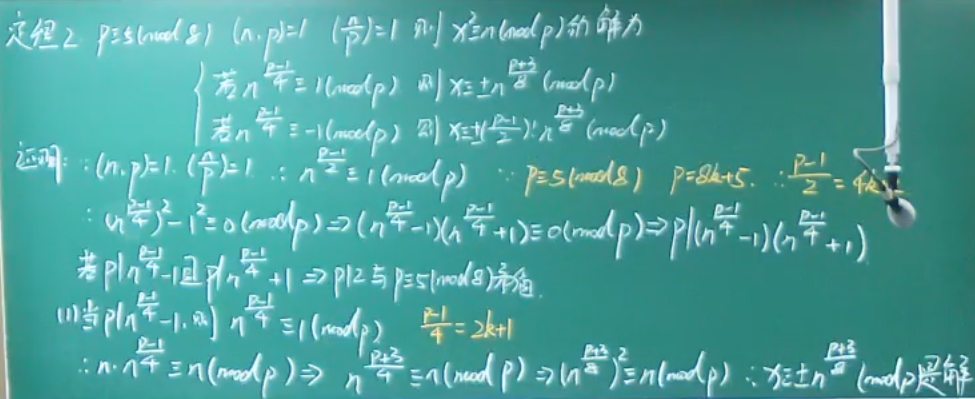
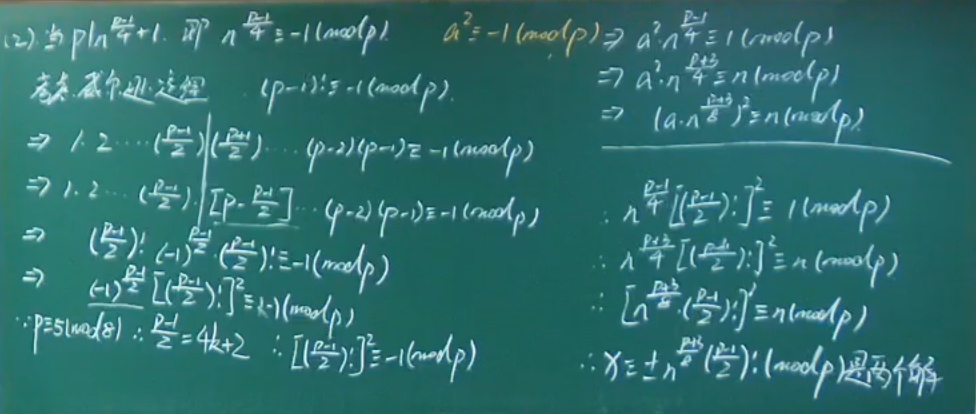









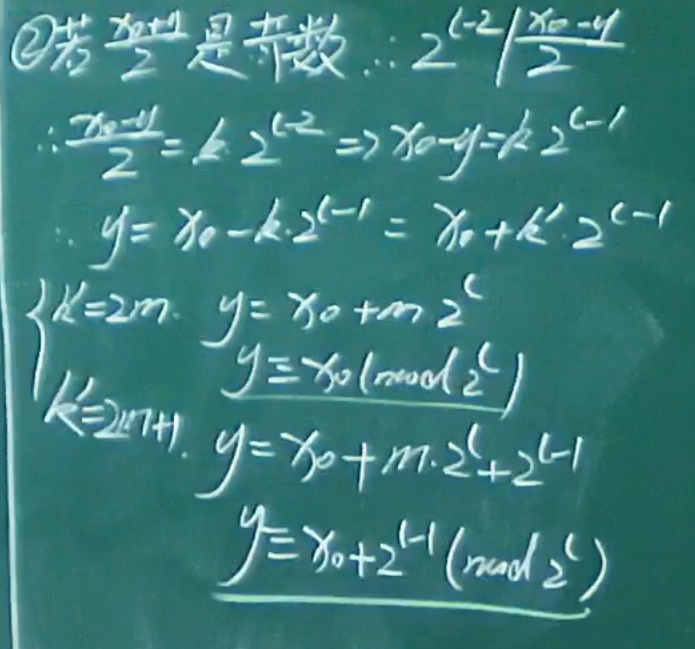
例题
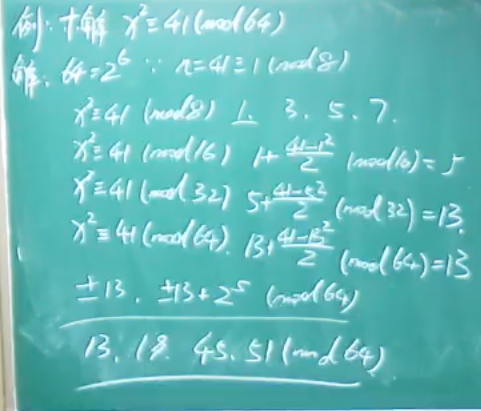
雅可比符号

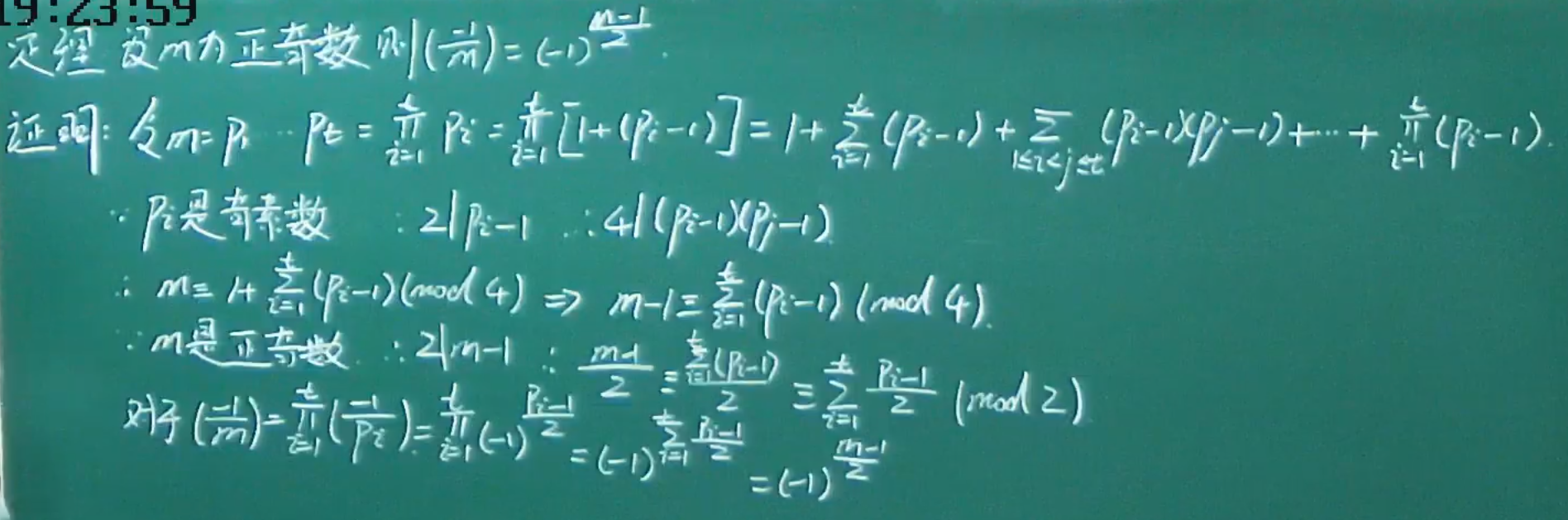



例题

- 结果是-1
原根
整数的次数





原根




计算次数的方法

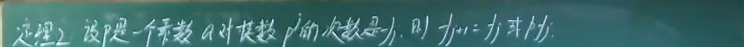
原根的计算方法


