简单记录一些与神经网络有关的基础知识
卷积公式
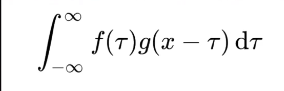
图像的卷积操作
图像是f 卷积核是g
卷积的神经网络
卷积价值:
- 一个系统,输入不稳定,输出稳定,用卷积求系统存量
- 一个卷积核可以规定一个像素点的周围像素点如何对它产生影响
- 一个过滤器作用的卷积核可以规定一个像素点如何试探周围的像素点从而筛选图像的特征
感知机
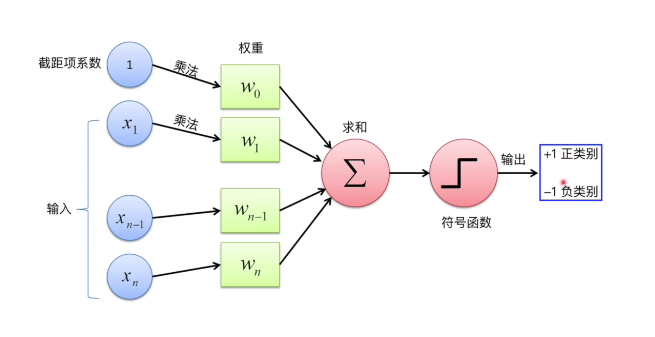
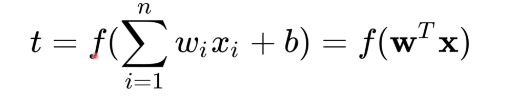
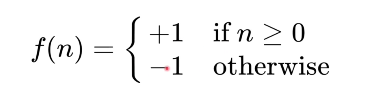
作用:通过线性划分来对数据分类
简单理解:数据输入感知机后通过w和b进行线性运算得出z,将z输入激活函数,得出感知机的输出
感知机的缺陷
无法解决异或运算
解决
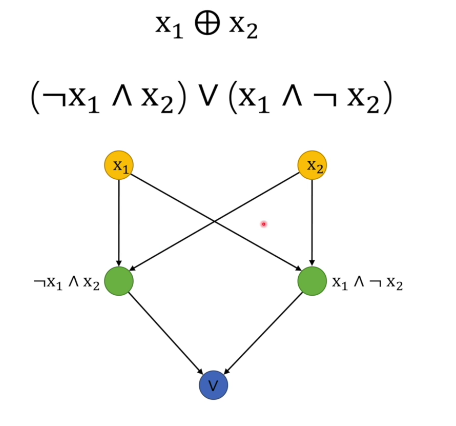
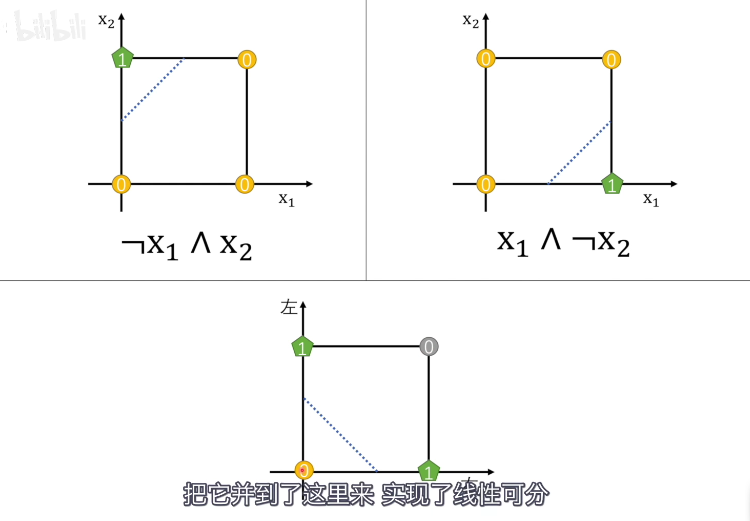
既然一个感知机解决不了异或运算,那就用多个感知机来解决
神经网络
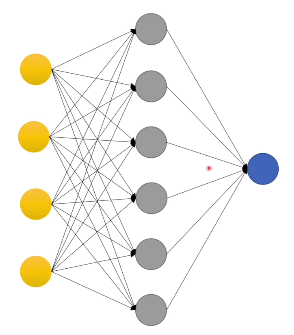
基本单元:感知机
训练神经网络:逼近一个统计模型
本质:线性函数+激活函数
线性函数感知机中的那个t公式
激活函数的作用是将无限制的输入转换为可预测形式的输出。一种常用的激活函数是sigmoid函数
sigmoid函数的输出介于0和1,我们可以理解为它把 (−∞,+∞) 范围内的数压缩到 (0, 1)以内。正值越大输出越接近1,负向数值越大输出越接近0。
信息量
一个事件从不确定到确定的难度
熵
一个系统从不确定到确定的难度,反映一个系统的混乱程度、
交叉熵
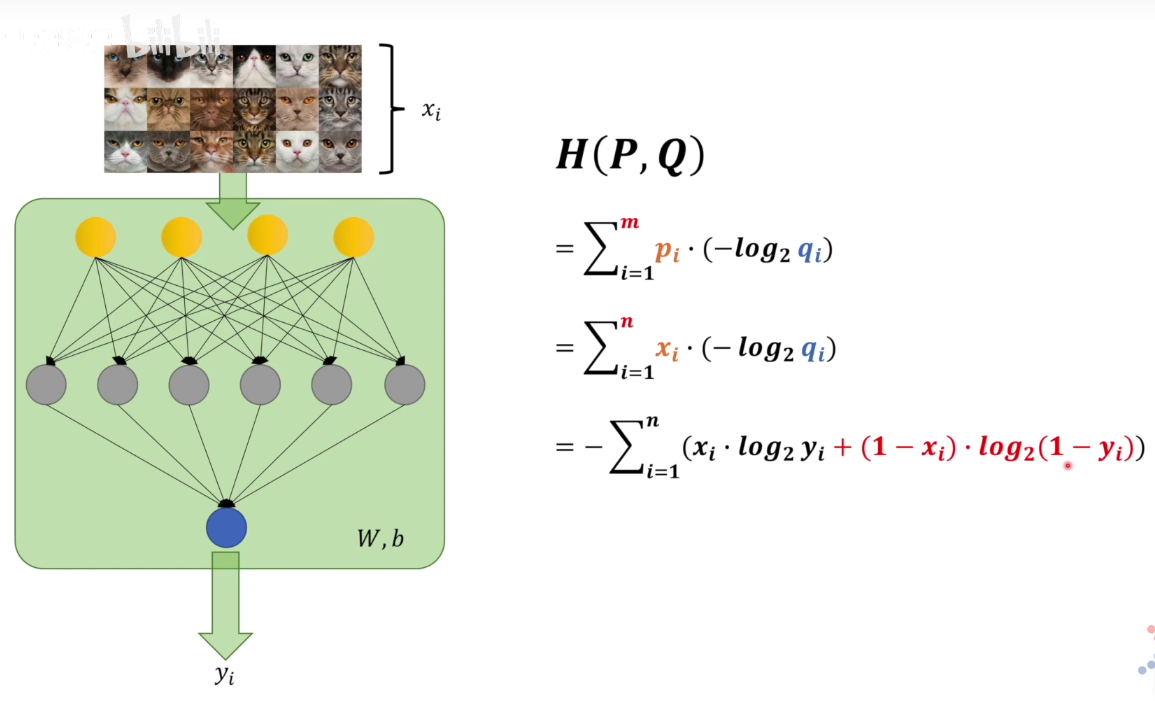
交叉熵越小,两个模型越相近
损失函数
神经网络中的标准模型和人脑中的标准模型相差多少的定量表达。具体可以用交叉熵来衡量,函数的两个参数中一个是人为标定的标准模型,一个是通过神经网络得到的标准模型
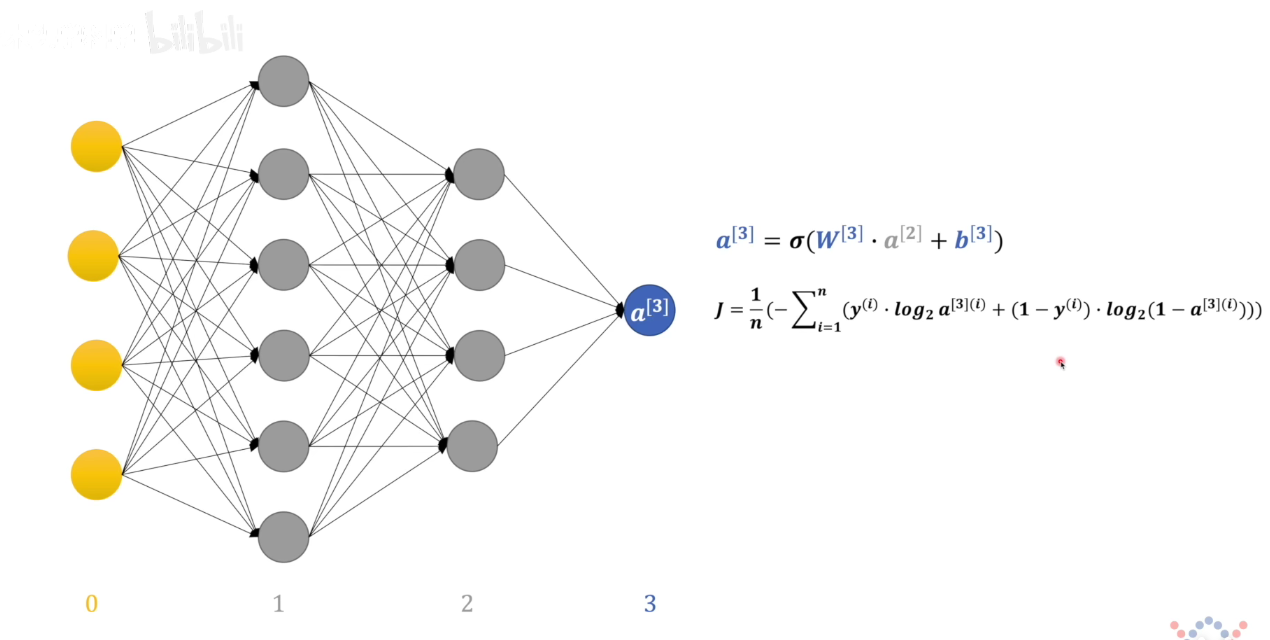
正向传播
把数据输入神经网络,这些数据会沿着神经网络正向传递,传递过程中会一层一层、一个一个地感知机操作(w,b参数起作用),最后得出一个结果
反向传播
将结果的偏差信息反向传递回各个参数上,根据这些参数对偏差的影响大小相应地修改
梯度
梯度指向的方向是数值增加最快的方向,反方向是数值减小最快的方向。
是一个向量的概念,有大小和方向。
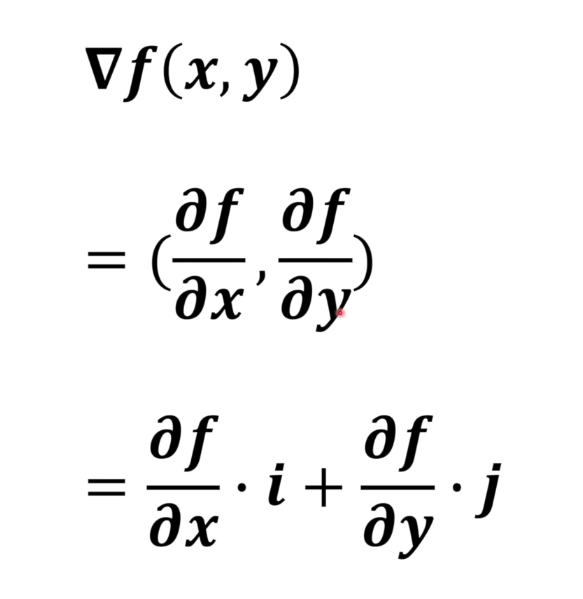
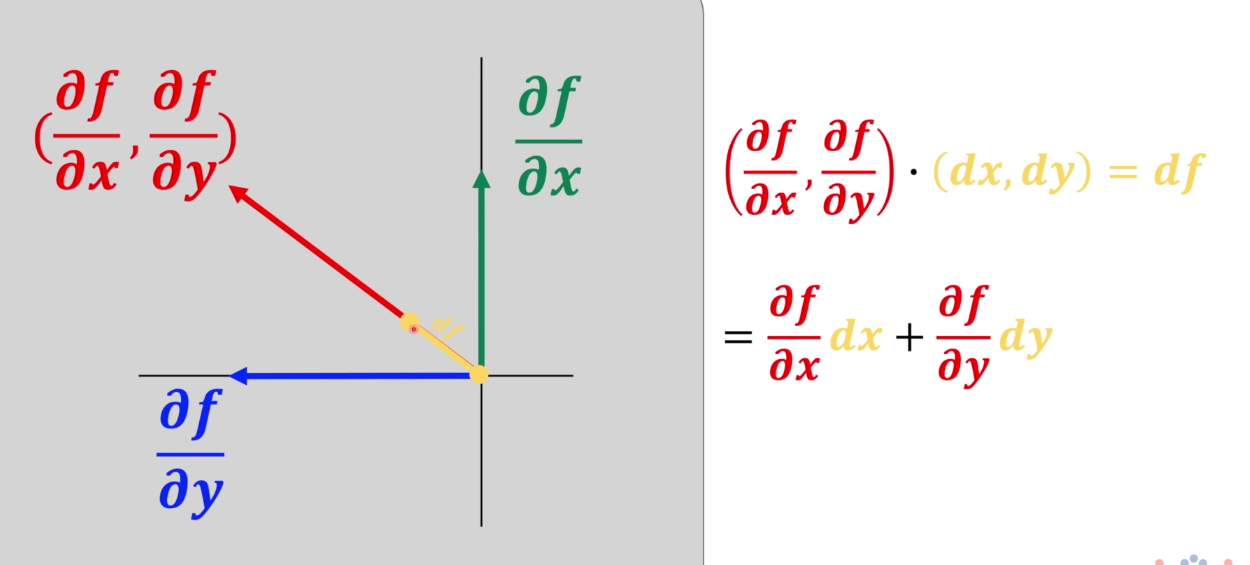
梯度下降法
梯度是损失函数的梯度
用到了反向传播的思想
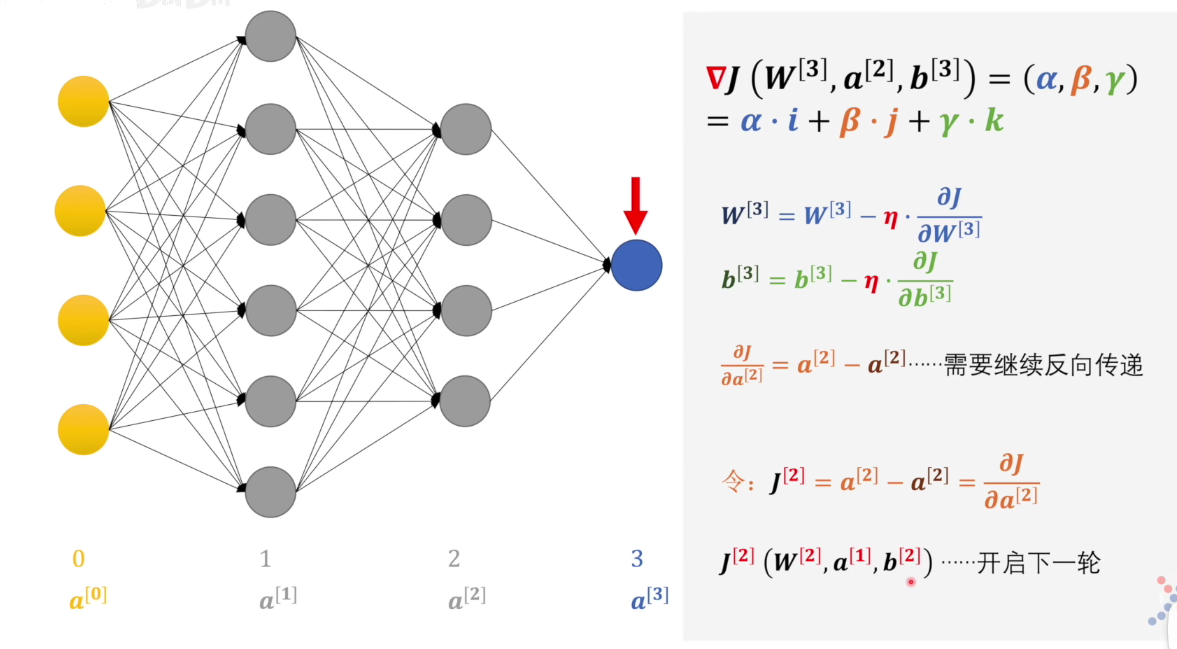
简单理解:把损失函数看作向量,把感知机的w系数,b偏置系数,a是上一层的输出进行分解后求分别偏导,更新w和b,η是学习率,a因为是上一层决定的,所以a移项后看作该层的“损失函数”继续反向传播(链式求导)
监督学习
监督学习是机器学习中的一种训练方式/学习方式
监督学习需要有明确的目标,很清楚自己想要什么结果。比如:按照“既定规则”来分类、预测某个具体的值
监督并不是指人站在机器旁边看机器做的对不对,而是下面的流程:
- 选择一个适合目标任务的数学模型
- 先把一部分已知的“问题和答案”(训练集)给机器去学习
- 机器总结出了自己的“方法论”
- 人类把”新的问题”(测试集)给机器,让他去解答
同构图和异构图
传统同构图(Homogeneous Graph)数据中只存在一种节点和边,因此在构建图神经网络时所有节点共享同样的模型参数并且拥有同样维度的特征空间。
而异构图(Heterogeneous Graph)中可以存在不只一种节点和边,因此允许不同类型的节点拥有不同维度的特征或属性。
理解
- 解释子图只能解释单个节点,而决策树可以构建全局性可解释,而且可以修正解释子图,让同类别的节点的解释子图更相似
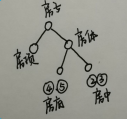
- 邻接矩阵本来是0和1 为了让邻接矩阵可以更新梯度 存储成张量的形式了
- 信息增益只是一种度量方式 不是一个具体的算法
- 是用已经分类好的数据集来构建决策树
参考资料