整除
初等数论的基本研究对象是:
- 整数集合(包括正整数、零、负整数)
- Z={0,±1,±2,……}
- 自然数集合(正整数集合)
- N={1,2,……}或者Z+={1,2,……}
整除的概念
整除的定义

- a=bc,a大b小,a是b的倍数,b是a的因数,称b整除a,记为b|a

整除的基本性质






例题


带余除法定理





例题


- 15能够整除255,余数为0

- 余数一定是≥0的
最大公因数
最大公因数的定义

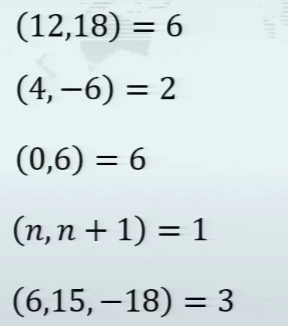
互素

最小公倍数的定义

最大公因数与最小公倍数基本性质



- 用来化简最大公因数的主要方法

例题


最大公因数和最小公倍数的本质属性定理





最大公因数表达式定理



算术基本定理
素数

算数基本定理


正整数的素因数标准分解式


例题


Euclid算法



- 求到最后余数为0,最后一个不为0的余数就是它俩的最大公因数
例题⭐

- 求最大公因数
- 求二元一次方程

筛法
筛法的依据定理



- 考试会用,实际不用
例题
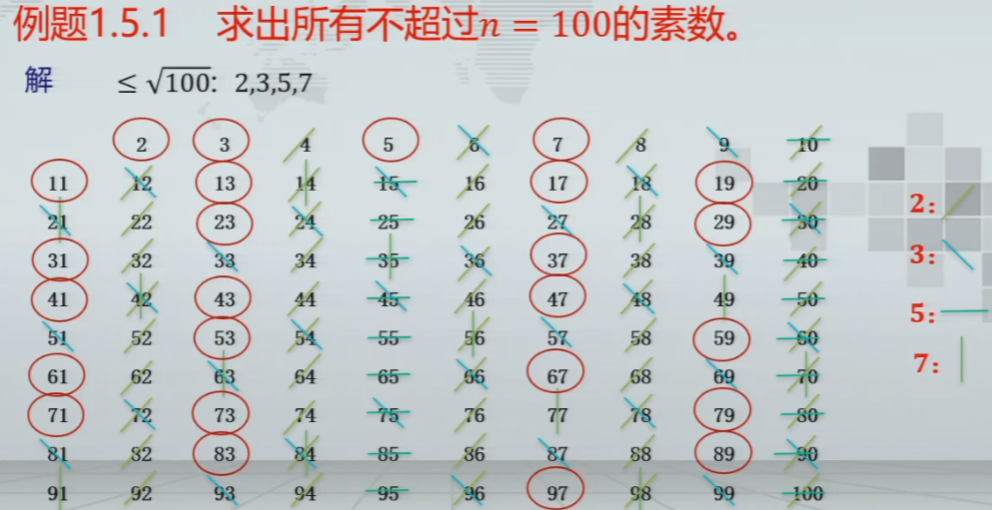
- 剔除2357的倍数,剩下的是素数

- 如果对任意的素数p≤√n,p都不是n的因数,那么n一定是素数。
同余
同余的概念
同余的定义


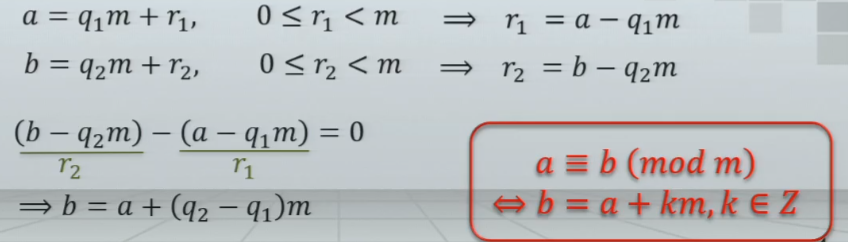

- 这四个中只要有一个成立,默认其余三个都成立

同余的等价关系定理



(3)若ab模m同余,则(a,m)=(b,m)



同余式和同余式组的关系定理

运算

- 先模后运算


例题

- 考试不让带计算器,模数不会这么大
模逆存在定理

- 前提条件是a和m互素
模逆运算

- 以上面的例子来说,虽然5和12都为3对模7的逆(看着和模逆存在的唯一性矛盾),但5和12在模7意义下相同,因为同余,所以一般说讨论比模数小的1-6和谁同余就行
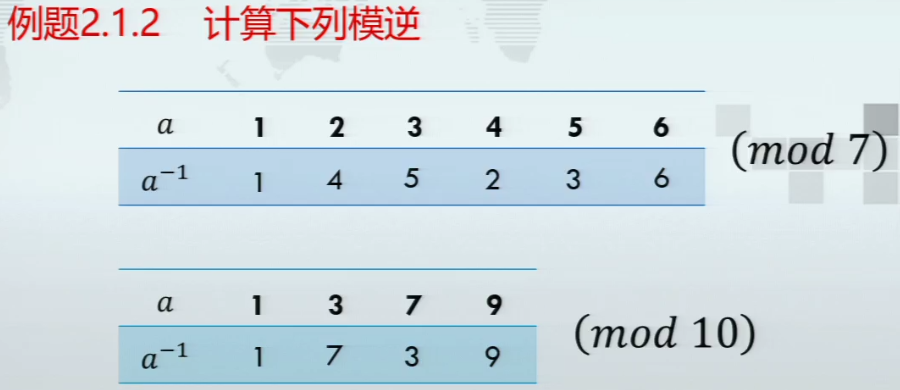

例题


同余类和既约同余类
同余类和完全剩余系



- 完全剩余系不唯一
既约同余类和既约剩余系

- 既约同余类的代表元与其互素,类里面的每个元素都互素

同余类的加法和乘法运算

例题
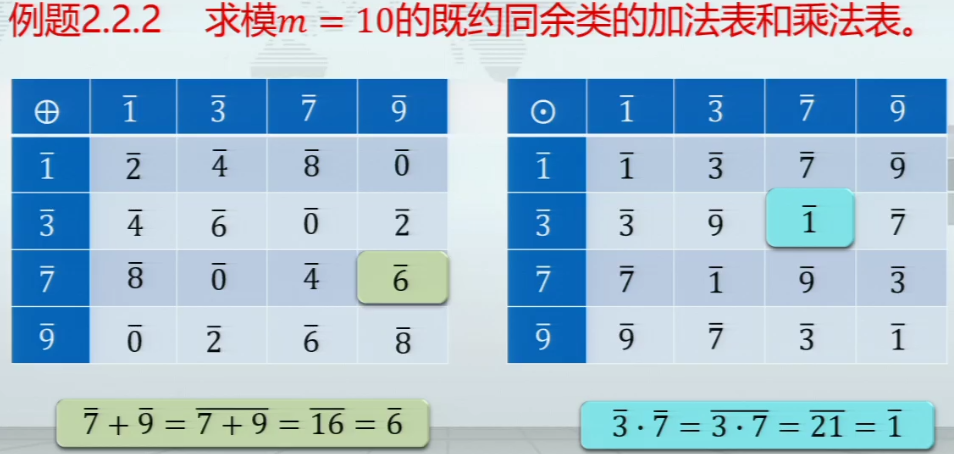
欧拉函数









- 这是这章的关键

例题

欧拉定理和费马小定理
Euler定理

例题
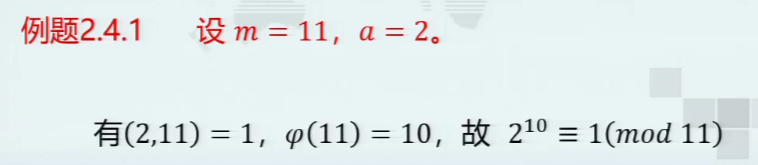


费马小定理

例题⭐

- 这种题一定要会做:根据欧拉定理算大模指数运算(大指数)
- 模数是偶数——欧拉定理
素性检测算法
Fermat小定理


Fermat素性检测

- 合数100%判断,素数概率判断
例题

- a可以随机选,演示用选的小
Miller-Rabin素性检测




- 包含模指数运算
RSA公钥加密算法

- 1978年,美国麻省理工学院的学者Rivest、Shamirz和Adleman提出了RSA公钥加密算法。是目前应用最广泛的公钥加密方案之一
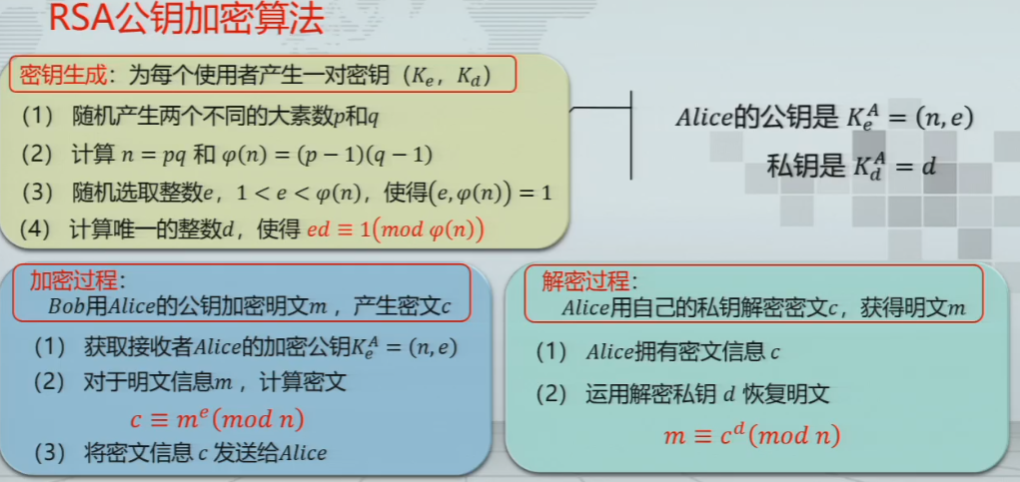

- 正确性



- 涉及:模乘、欧拉函数、欧几里得算法、随机数生成算法、模指数算法……
同余方程
一次同余方程
二元一次不定方程






一次同余方程整数解定理


例题




- 自己手算一遍
- 例3.1.6也可用Eulide算法求模逆
基于同余方程的仿射加密算法

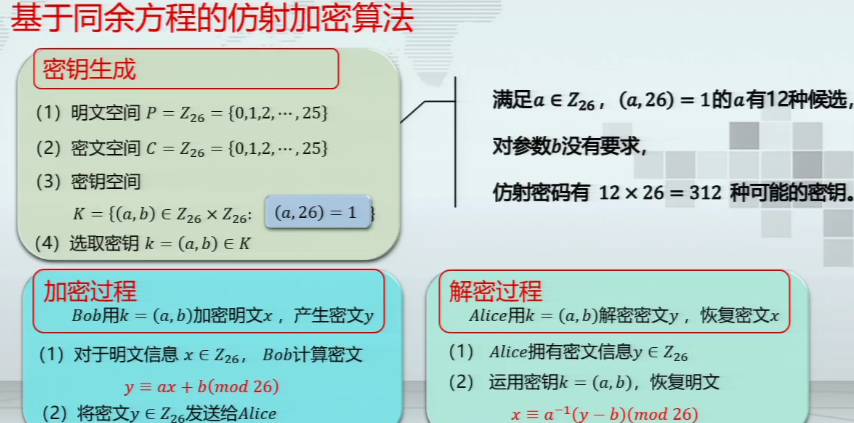
例题

中国剩余定理
- 重点

- 用中国剩余定理的条件:
- 模数互素
- x系数为1


例题⭐

- 也可以用Eulide算法求逆
- 同余式和同余式组是等价的,前提是同余式组的模数的最大公因数是1
- 59x≡27(mod 7) <=> 3x≡27(mod 7);59/7…3
- 3x≡27(mod 7) <=> 3x≡6(mod 7);27/7…6
- 3x≡6(mod 7) <=> x≡2(mod 7);(3,7)=1
- 59x≡27(mod 13) <=> 7x≡27(mod 13);59/13=4…7
- 7x≡27(mod 13) <=> 7x≡1(mod 13);27/13=2…1
- 7x≡1(mod 13) <=> x≡7-1×1(mod 13);(7,13)=1
- x≡7-1×1(mod 13) <=> x≡7-1(mod 13) <=> x≡2(mod 13);2×7=14;14/13=1…1
- 处理后,x的系数都为1,模数两两互素
- 13M1-1≡1(mod 7) <=> M1-1≡6(mod 7);13/7=1…6;6×6=36;36/7=5…1;or 13×6=78/7=11…1
- 7M2-1≡1(mod 13) <=> M2-1≡2(mod 13);7/13=0…7;7×2=14;14/13=1…1;or 7×2=14/13=1…1
- x≡13×6×2+7×2×2(mod 91) <=> x≡2(mod 91);13×6×2+7×2×2=184/91=2…2


- 不能用中国剩余定理:x系数不是1,(12,10)≠1
- 5x≡7(mod 3) <=> 2x≡1(mod 3);5/3…2;7/3…1
- x≡2-1(mod 3) <=> x≡2(mod 3);(2×2)/3…1
- 2和4不互素,去掉一个方程;去掉模2的方程,因为模2方程的解为1,3,5,7,9,模4方程的解为7,11,15,19;显然模4的解包含在模2解中;但方程组的解需要满足所有方程;而模2方程的一些解不满足模4的方程,故去掉模2的方程
- 同余式化为同余式组是,同余式组模数的最小公倍数是同余式的模数=>[12,10]=60,所以最后的解要模60

- 253能被分解=>中国剩余定理
- 看欧拉定理
- 模数不是素数=>分解开=>中国剩余定理
- 中国剩余定理解决:x系数是1,模数两两互素的一次同余方程组
基于中国剩余定理的秘密共享算法
秘密共享是将秘密以适当的方式拆分,拆分后的每一个子秘密由不同的参与者管理,单个参与者无法恢复秘密信息,只有若干个参与者一同协作才能恢复秘密消息。并且,当其中某些参与者出问题时,秘密仍可以恢复。






二次剩余
二次剩余




例题

- 欧拉判别的模指数运算麻烦,所以引入Legendre符号
Legendre符号
Legendre符号的定义
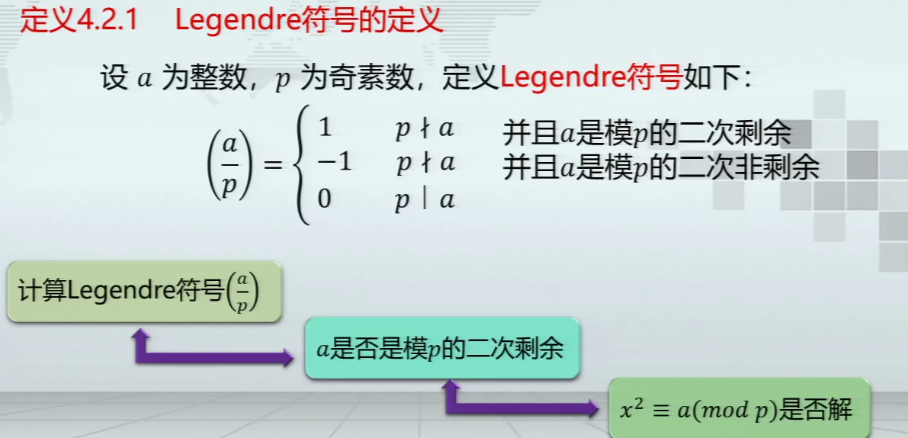
- 讨论极简形式的二次剩余方程是否有解
- 欧拉判别的模指数运算麻烦,所以引入Legendre符号

Legendre符号的欧拉判别法

Legendre符号的性质定理


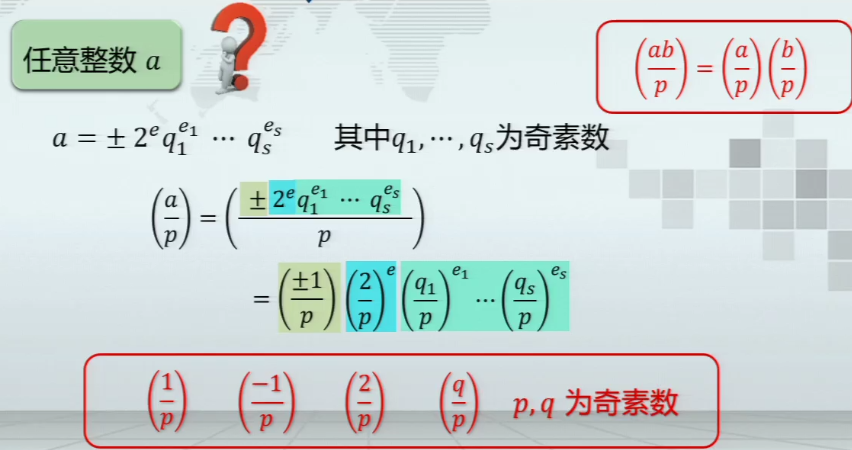
- 乘积的legendre符号=legendre符号的乘积
- 对a进行标准素因数分解
Legendre符号的计算公式定理⭐

- 这三个公式要会背






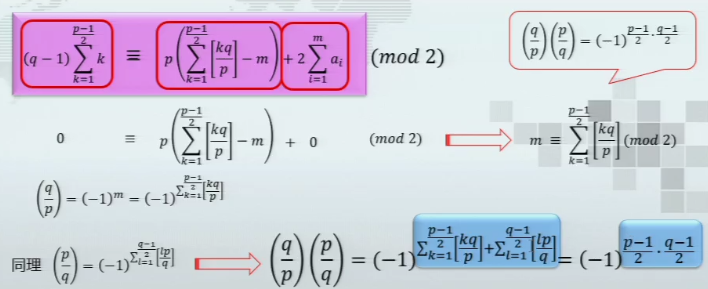
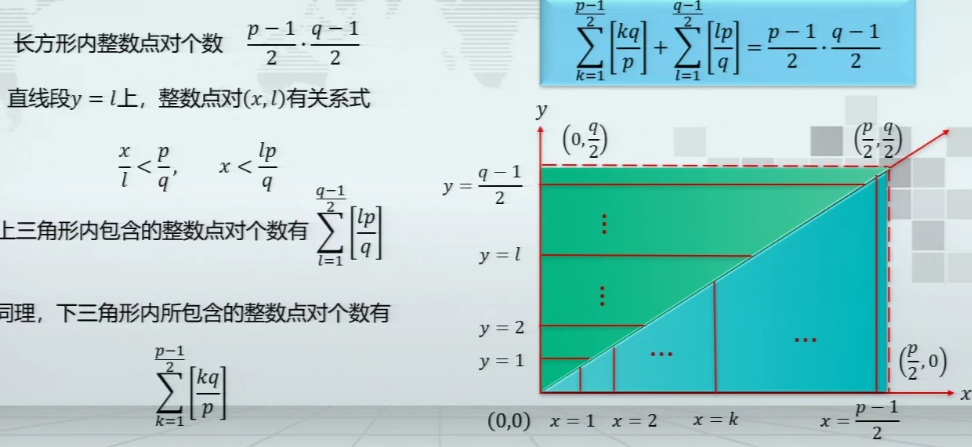
例题

- 首先模227要是一个奇素数,用第一章最后的筛法
- 标准素因数分解,15被分成3×5
- 3和227都是奇素数=>二次互反律
- -(-1/3) => p=3 => 是第二个公式的第二种情况 => -(-1) => 1

- 用到第一个公式和奇偶分情况
Jacobi符号

Jacobi符号的定义







例题

- 相比Legendre符号,Jacobi符号不用素因数分解

Robin公钥加密算法


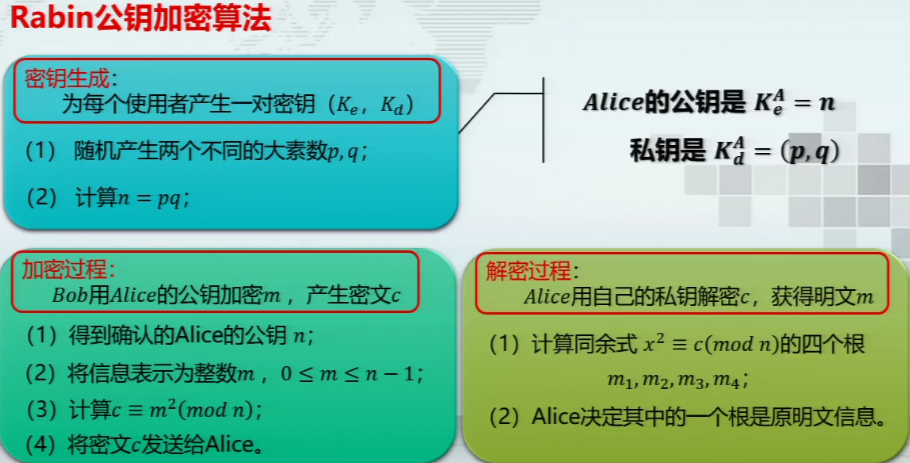


原根


原根的概念
阶的定义
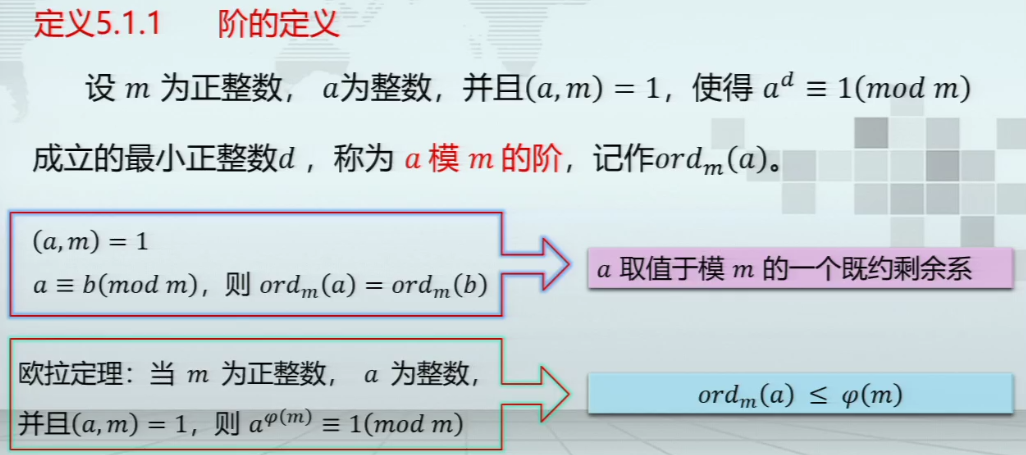
原根的定义

例题

阶的性质定理


原根的性质定理



例题




例题


阶的计算
- 不考


例题
- 不考,主要靠程序计算实现


原根的计算
- 不考


例题
- 不考,主要靠程序计算实现




离散对数问题
- 重点
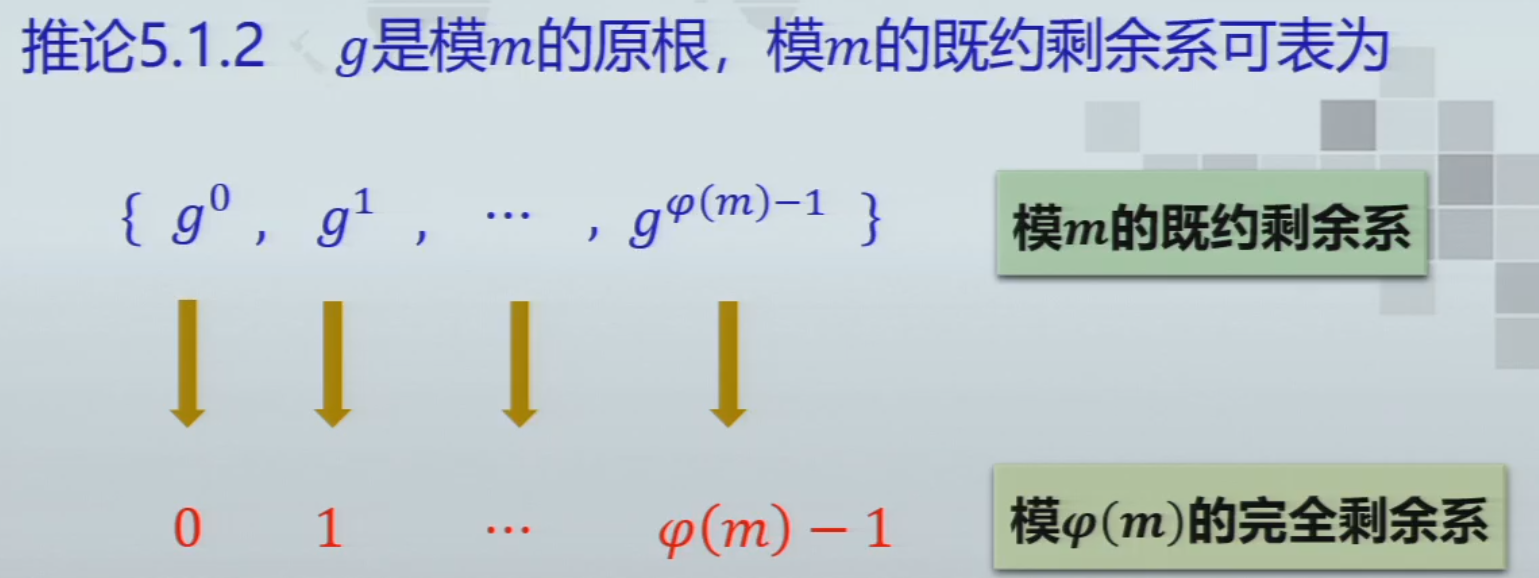
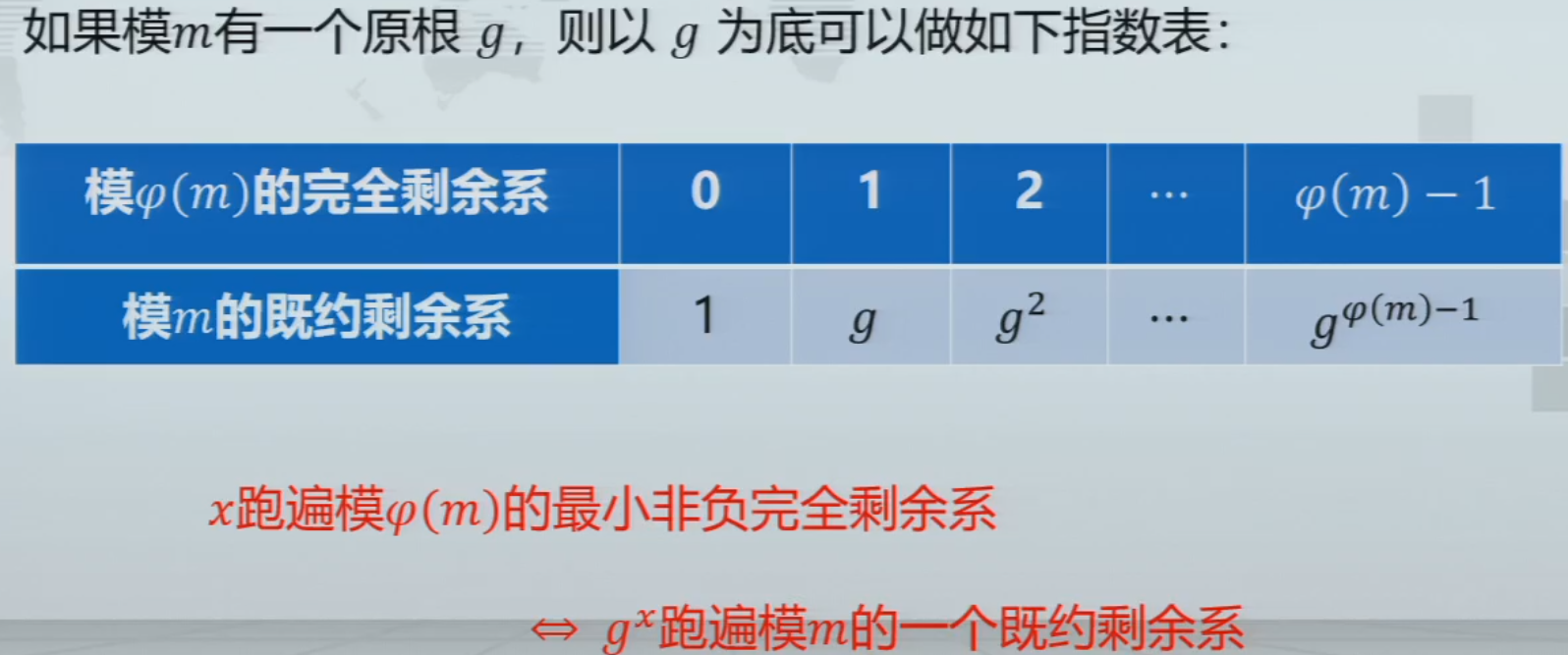



Diffie-Hellman秘钥协商算法
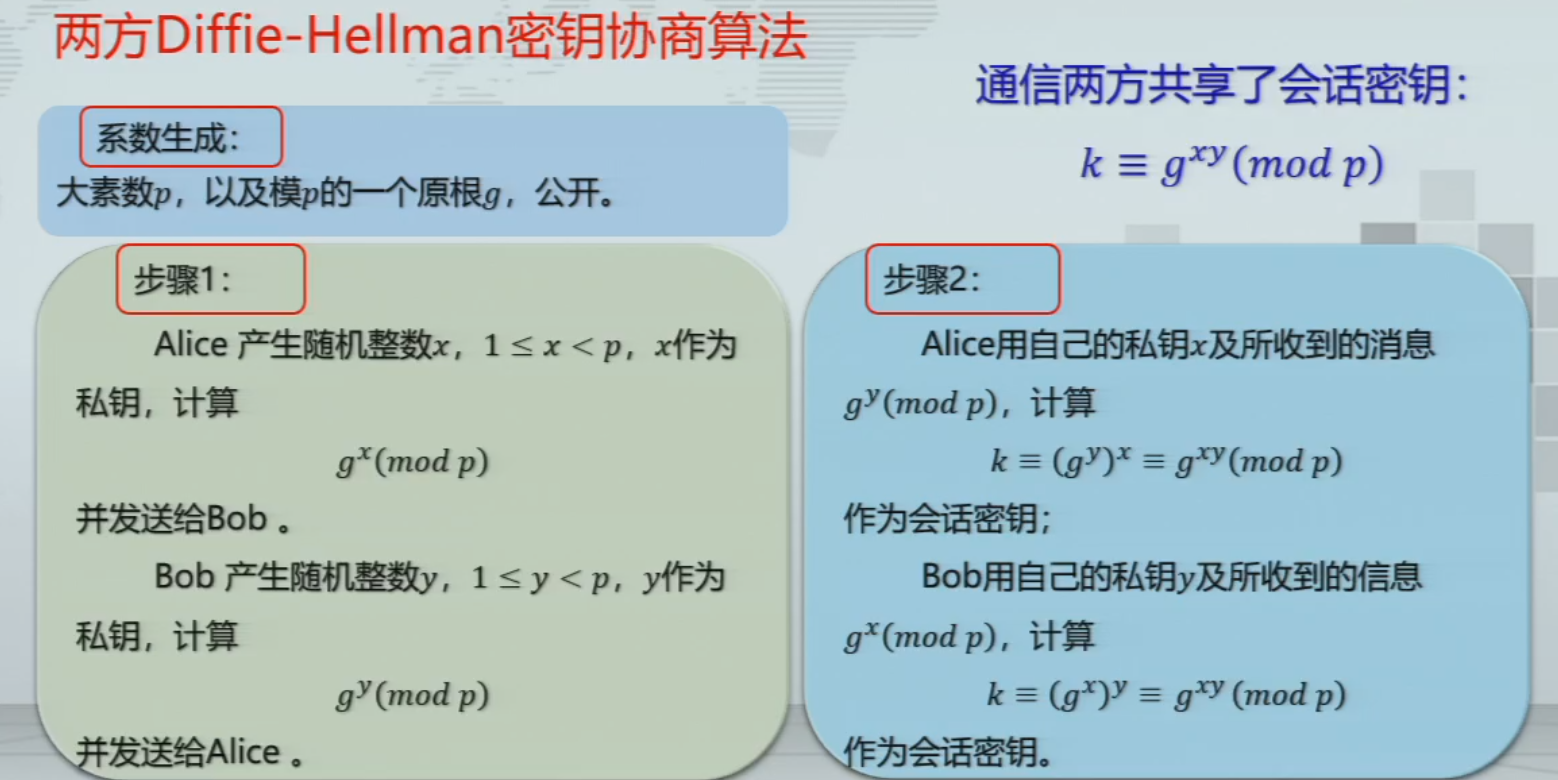
- 单独用有问题,会被攻击

群
代数系统:
- 非空集合
- 代数运算
群

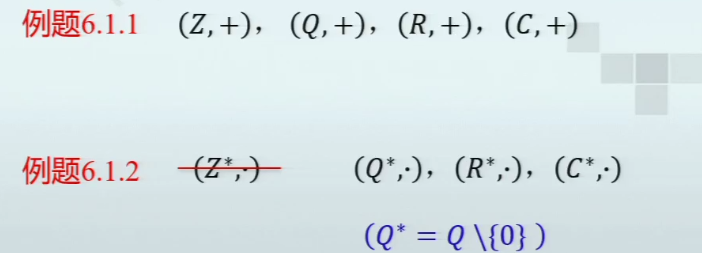




- 从后往前,后面1对应3,前面3对应3,所以1对应3;后面3对应2,前面2对应1,所以3对应1,故(1,3)

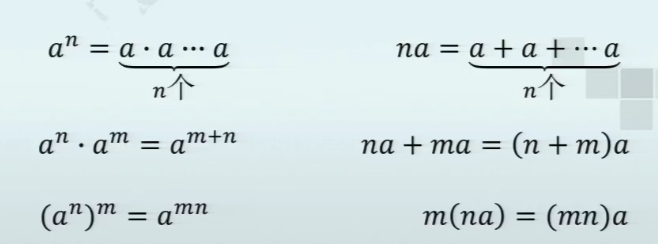
子群















商群





群同态



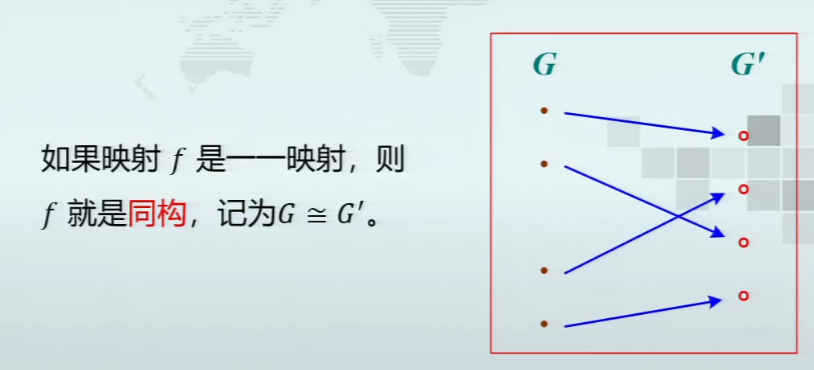




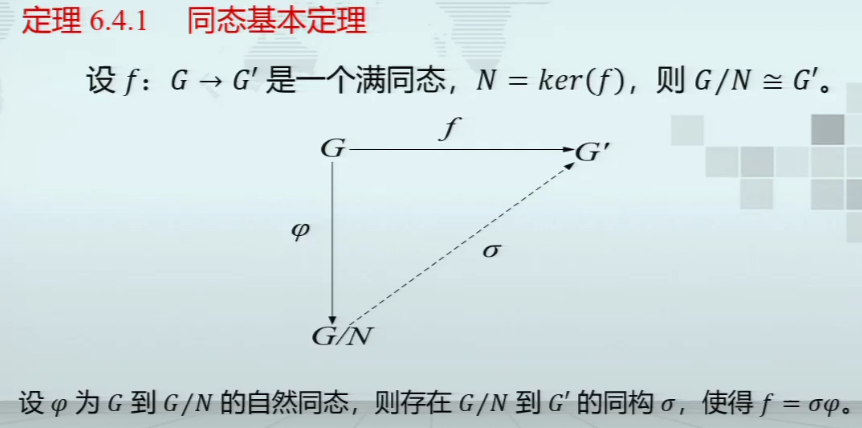

循环群





环和域
环




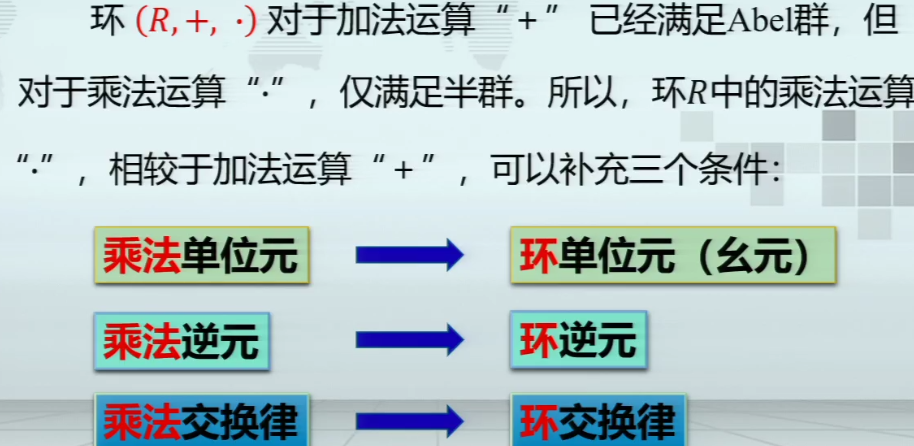
域






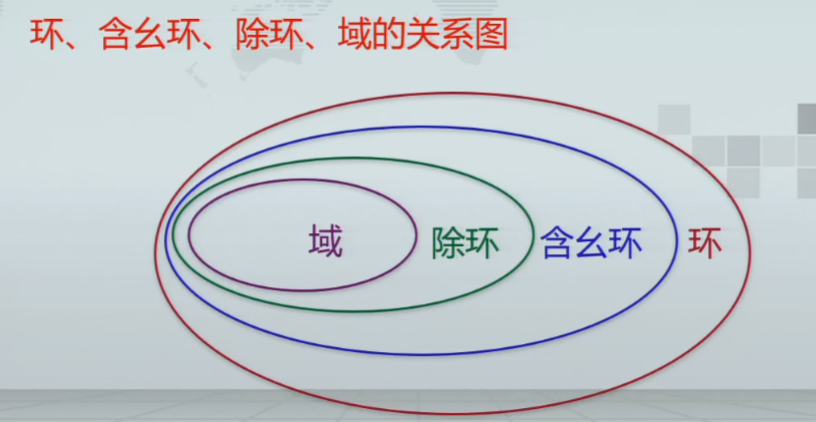
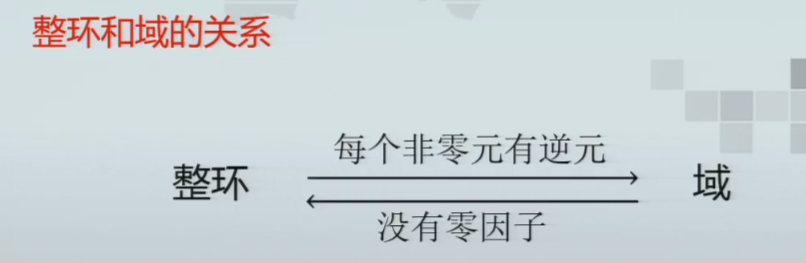


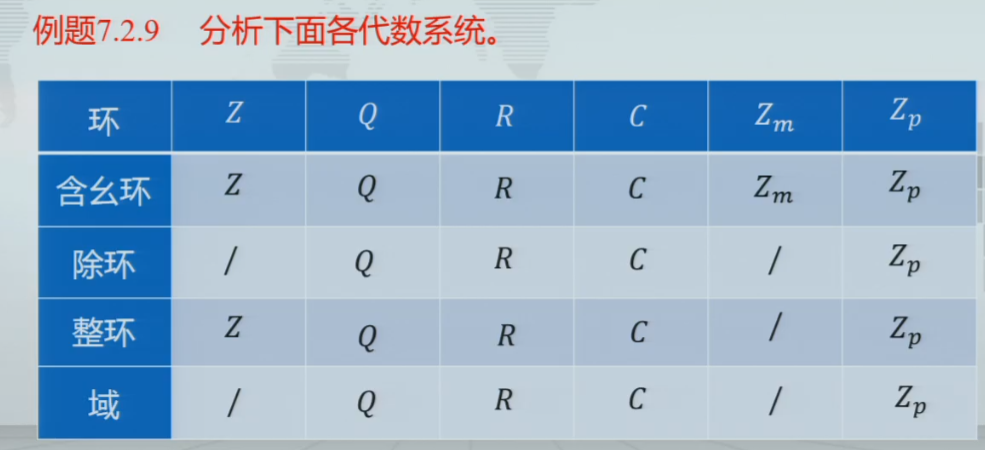
子环





商环



环同态



多项式环
多项式环的概念









域上的多项式环










最大公因式和最小公倍式





不可约多项式





有限域
有限域的加法特性




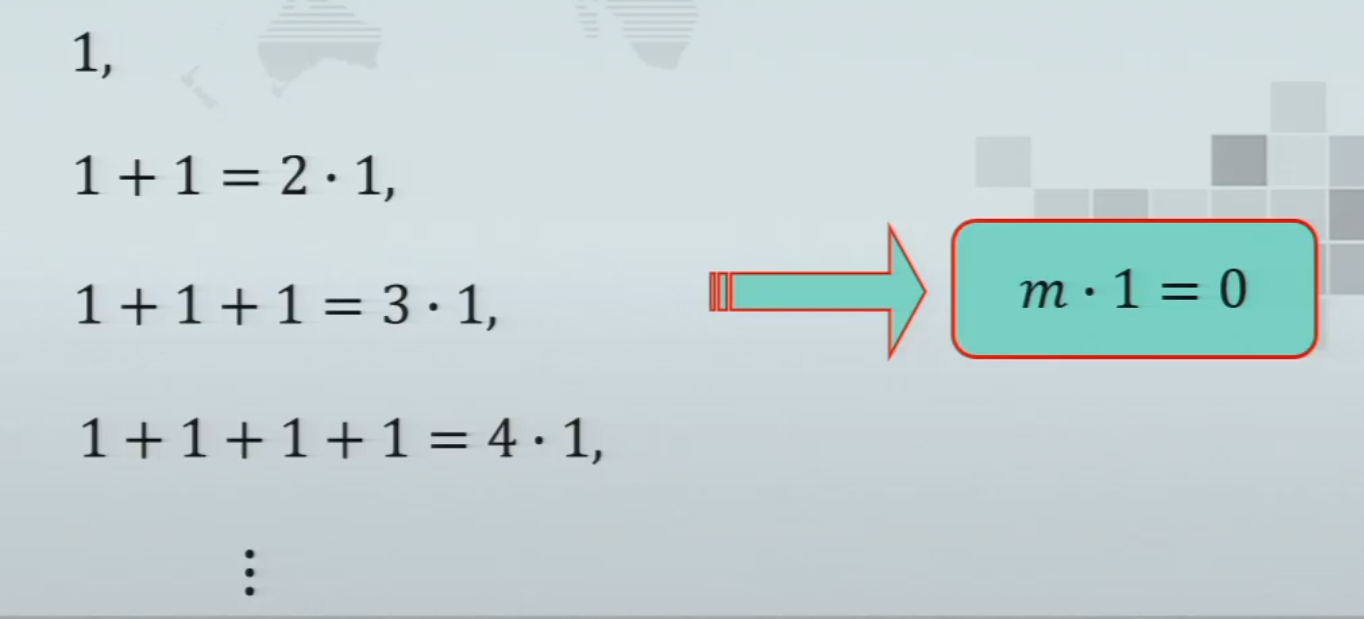




有限域的乘法特性



扩域



















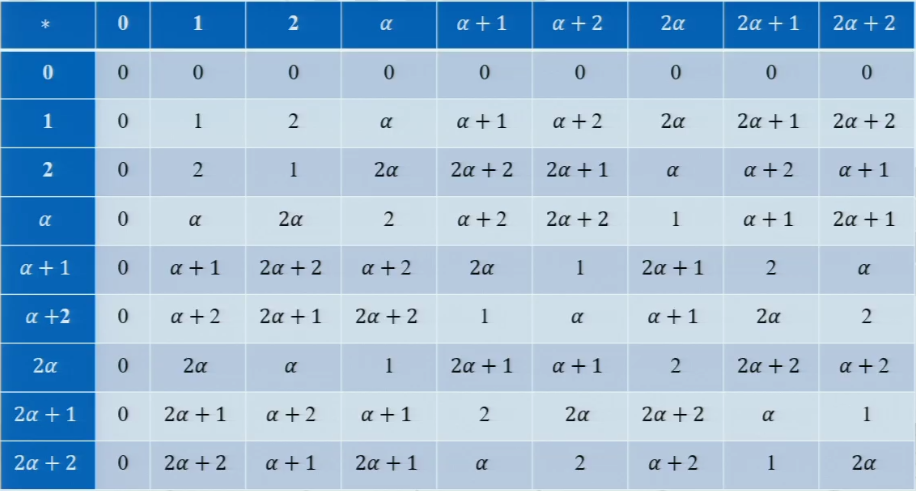
有限域域元素表示
- 要求搞清楚有限域域元素的计算















有限域的本原元







有限域的多项式















椭圆曲线
椭圆曲线







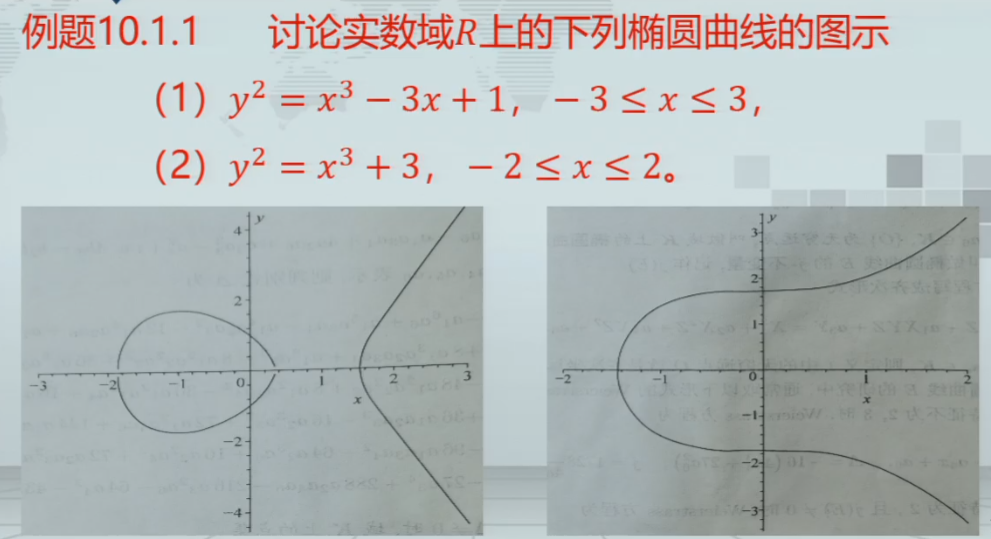


加法原则
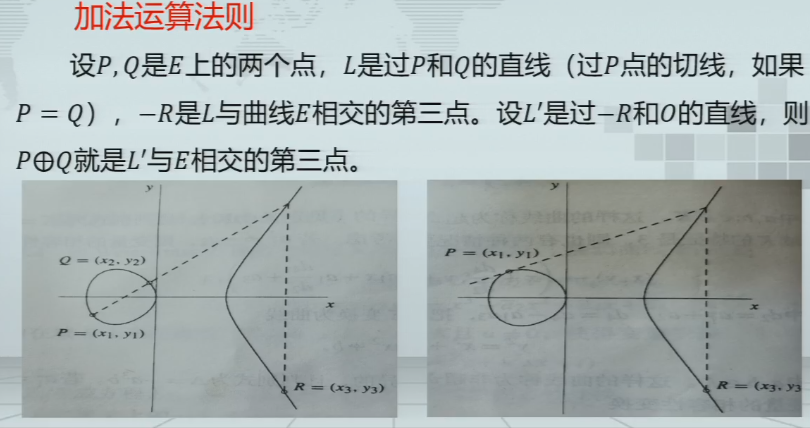



椭圆曲线点加群


⭐
椭圆曲线点的运算必考,例题10.3.2






k倍点运算







椭圆曲线离散对数问题






