LeetCode 0106.从中序和后序遍历序列构造二叉树

从中序和后序遍历序列构造二叉树

LeetCode106. 从中序与后序遍历序列构造二叉树

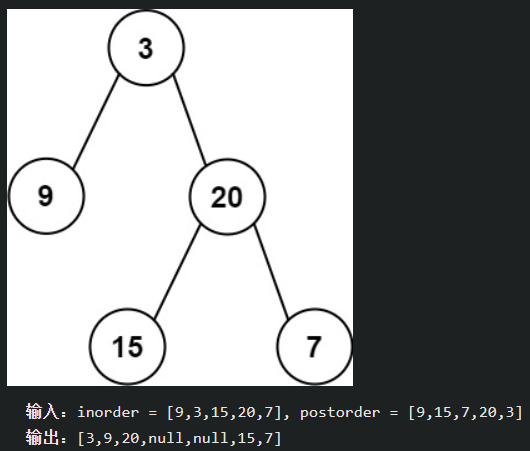
给定两个整数数组inorder和postorder，其中inorder是二叉树的中序遍历，postorder是同一棵树的后序遍历，请你构造并返回这颗二叉树

思路

根据两个顺序构造一个唯一的二叉树：以后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来再切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素

说到一层一层切割，就应该想到了递归。来看一下一共分几步：

第一步：如果数组大小为零的话，说明是空节点了。
第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
第四步：切割中序数组，切成中序左数组和中序右数组（顺序别搞反了，一定是先切中序数组）
第五步：切割后序数组，切成后序左数组和后序右数组
第六步：递归处理左区间和右区间

注意：前序和后序不能唯一确定一棵二叉树！，因为没有中序遍历无法确定左右部分，也就是无法分割

代码

Go

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


func buildTree(inorder []int, postorder []int) *TreeNode {
    //若为空数组,则返回nil
    if len(inorder) < 1 || len(postorder) < 1 {
        return nil
    }
    //先找到根节点（后续遍历的最后一个就是根节点）,保存节点值到nodeValue
    nodeValue := postorder[len(postorder)-1]
    //从中序遍历中找到一分为二的点，左边为左子树，右边为右子树
    midIndex := findRootIndex(inorder, nodeValue)
    //构造root
    root := &TreeNode{Val: nodeValue,
                      //将后续遍历一分为二，左边为左子树，右边为右子树
                      Left:  buildTree(inorder[:midIndex], postorder[:midIndex]), 
                      Right: buildTree(inorder[midIndex+1:], postorder[midIndex:len(postorder)-1])}
    return root
}

//从中序数组中找到中间节点的索引
func findRootIndex(inorder []int, target int) (index int) {
    for i := 0; i < len(inorder); i++ {
        if target == inorder[i] {
            return i
        }
    }
    return -1
}

Link

GitHub