返回
Algorithm 基础能力

十大排序算法

前言

排序算法作为一项需求，它足够简单，是学习基础算法思想（例如：分治算法、减治思想、递归写法）很好的学习材料。如果是面试遇到写排序算法，一般还是先问清楚数据的特点，有的时候可能还会给具体的业务场景，在面试官肯定采用的算法之后再编码，不要一上来就手撕

学习算法的可视化网站：https://www.cs.usfca.edu/~galles/visualization/Algorithms.html，点到 Sorting 这一章节，会看到 10 大排序算法，而且还是交互式的。建议先了解算法的思路，再去理解代码是怎么写的。

《算法 4》和《算法导论》介绍的算法思想足够经典，但不是最新研究结果，也并非最快。如果想研究最新排序算法的结论，可以参考最新的学术论文，或者是在互联网上搜索相关资料，或者是查看当前所使用编程语言关于排序部分的源代码。《算法 4》和《算法导论》不是面向笔试和面试的书籍，可以把它们作为参考书，遇到什么知识点不会了，再去查，除非是专业的研究人员，看这两本书的时候建议忽略其中的数学证明和公式，只挑对自己有用的部分来看

912. 排序数组 - 力扣（LeetCode）

给定一个整数数组 nums，将该数组升序排列

选择排序

了解

思路：每一轮选取未排定部分中最小的元素交换到未排定部分的最开头，经过若干个步骤，就能排定整个数组。即：先选出最小的，再选出第 2 小的，以此类推。

两层循环，外层循环遍历给定数组，内层循环从外层索引开始查找最小值，找到后交换到外层索引

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

func sortArray(nums []int) []int {
    for i := range nums {
        minIndex := i
        for j := i; j < len(nums); j++ { // 找最小值
            if nums[j] < nums[minIndex] {
                minIndex = j
            }
        }
        nums[i], nums[minIndex] = nums[minIndex], nums[i] // 交换
    }
    return nums
}

总结：

  • 算法思想 1：贪心算法：每一次决策只看当前，当前最优，则全局最优。注意：这种思想不是任何时候都适用。

  • 算法思想 2：减治思想：外层循环每一次都能排定一个元素，问题的规模逐渐减少，直到全部解决，即「大而化小，小而化了」。运用「减治思想」很典型的算法就是大名鼎鼎的「二分查找」。

  • 优点：交换次数最少

「选择排序」看起来好像最没有用，但是如果在交换成本较高的排序任务中，就可以使用「选择排序」。适用于交换成本高的排序任务

建议不要对算法带有个人色彩，在面试回答问题的时候和看待一个人和事物的时候，可以参考的回答模式是「具体问题具体分析，在什么情况下，用什么算法」。

复杂度分析：

  • 时间复杂度：O(N2)O(N^2)，这里 NN 是数组的长度；
  • 空间复杂度：O(1)O(1)，使用到常数个临时变量。
  • 不稳定：相同元素，后面的会被放到前面

插入排序⭐

熟悉

思路：每次将一个数字插入一个有序的数组里，成为一个长度更长的有序数组，有限次操作以后，数组整体有序。在接近有序的情况下，插入排序表现优异

img

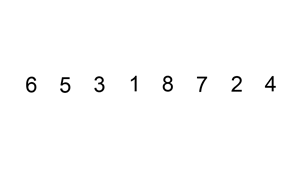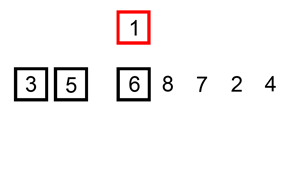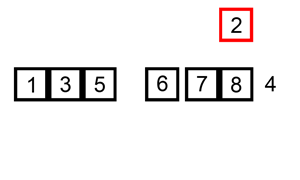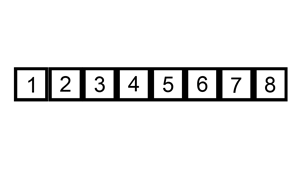
两层循环，外层循环从第二个元素开始遍历给定数组，内层循环向前遍历，将当前元素前面比当前元素大的元素后移一个单位，直到找到小于或等于当前元素的元素，将当前元素插入到该元素后面

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

func sortArray(nums []int) []int {
    for i := 1; i < len(nums); i++ {
        // 保存当前元素
        temp := nums[i]
        // 从当前元素开始向前遍历
        j := i
        for ; j > 0 && nums[j-1] > temp; j-- {
            // 遍历元素的前一个元素后移一个单位
            nums[j] = nums[j-1] 
        }
        // 插入保存的当前元素
        nums[j] = temp 
    }
    return nums
}

  • 特点：「插入排序」可以提前终止内层循环（体现在 nums[j - 1] > temp 不满足时），在数组「几乎有序」的前提下，「插入排序」的时间复杂度可以达到 O(N)O(N)；

  • 由于「插入排序」在「几乎有序」的数组上表现良好，特别地，在「短数组」上的表现也很好。因为「短数组」的特点是：每个元素离它最终排定的位置都不会太远。为此，在小区间内执行排序任务的时候，可以使用「插入排序」。

复杂度分析：

  • 时间复杂度：O(N2)O(N^2)，这里 NN 是数组的长度；
  • 空间复杂度：O(1)O(1)，使用到常数个临时变量。
  • 稳定排序

归并排序🌟

重点

  • 基本思路：借助额外空间，合并两个有序数组，得到更长的有序数组。例如：「力扣」第 88 题：合并两个有序数组。

  • 算法思想：分而治之（分治思想）。「分而治之」思想的形象理解是「曹冲称象」、MapReduce，在一定情况下可以并行化。

    • 分： 不断将数组从中点位置划分开（即二分法），将整个数组的排序问题转化为子数组的排序问题；
    • 治： 划分到子数组长度为 1 时，开始向上合并，不断将 较短排序数组 合并为 较长排序数组，直至合并至原数组时完成排序；

  • 「归并排序」是理解「递归思想」的非常好的学习材料，递归完成以后，合并两个有序数组，即「递归函数执行完成以后，还可以做点事情」

排序过程：进入归并排序函数后，先判断当前数组元素数是否等于1，若是则直接返回当前数组；若不是，则用当前数组的一半向左递归，另一半向右递归；两个递归执行完成后，得到两个子区间的有序数组，合并两个子区间，借助额外空间，逐个比较元素大小放入结果集中，直到一方结束，另一方剩下元素直接入集结束

排序过程优化：设定一个插入排序的门限值，元素数小于等于该值时，使用插入排序对小数组进行排序；进入归并排序函数后，先判断当前数组元素数是否小于等于门限值，若是则使用插入排序对数组排序后返回当前数组；若不是，则用当前数组的一半向左递归，另一半向右递归；两个递归执行完成后，得到两个子区间的有序数组，判断左区间末值是否小于等于右区间首值，若是说明两子区间本身有序直接返回，若不是则合并两个子区间，借助额外空间，逐个比较元素大小放入结果集中，直到一方结束，另一方剩下元素直接入集结束

  • 优化点一：在「小区间」里转向使用「插入排序」，不必直接递归二分到一个元素，Java 源码里面也有类似这种操作，「小区间」的长度是个超参数，需要测试决定，这里参考了 JDK 源码设置为7；
  • 优化点二：在「两个数组」本身就是有序的情况下，无需合并；

递归过程优化：设定一个插入排序的门限值，元素数小于等于该值时，使用插入排序对小数组进行排序；进入归并排序函数后，先判断当前数组元素数是否小于等于门限值，若是则使用插入排序对数组排序后返回；若不是，则用当前数组的一半向左递归，另一半向右递归，直到满足门限值后递归返回，两个递归返回完成后，给定数组区间被分为两个子区间的有序数组，判断左区间末值是否小于等于右区间首值，若是说明两子区间本身有序直接返回，若不是则合并两个子区间，借助额外空间，逐个比较元素大小，直到一方结束，另一方剩下元素直接入集结束

  • 优化点：不需要递归返回值，直接在原数组上完成排序

理解递归：不断二分出子区间，直到子区间满足门限值排序后，向上返回，每次返回得到一个有序左右子区间后就进行一次合并，最终返回整个有序数组

归并

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

func sortArray(nums []int) []int {
    res := mergeSort(nums)
    return res
}
func mergeSort(nums []int) []int {
    if len(nums) == 1 {
        return nums
    }
    left := mergeSort(nums[:len(nums)/2])
    right := mergeSort(nums[len(nums)/2:])
    return merge(left, right)
}
func merge(nums1, nums2 []int) []int {
    res := make([]int, len(nums1)+len(nums2))
    idx1, idx2 := 0, 0
    for i := range res {
        // nums1 遍历结束
        if idx1 == len(nums1) { 
            // nums2剩下直接入集
            res[i] = nums2[idx2] 
            idx2++
        } else if idx2 == len(nums2) {
            // nums2 遍历结束
            // nums1剩下直接入集
            res[i] = nums1[idx1] 
            idx1++
        } else if nums1[idx1] <= nums2[idx2] {
            res[i] = nums1[idx1]
            idx1++
        } else {
            res[i] = nums2[idx2]
            idx2++
        }
    }
    return res
}

归并+插入

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

const INSERTION_SORT_THRESHOLD = 7

func sortArray(nums []int) []int {
    res := mergeSort(nums)
    return res
}
func mergeSort(nums []int) []int {
    if len(nums) <= INSERTION_SORT_THRESHOLD {
        res := insertSort(nums)
        return res
    }
    left := mergeSort(nums[:len(nums)/2])
    right := mergeSort(nums[len(nums)/2:])
    if left[len(left)-1] <= right[0] {
        res := append(left, right...)
        return res
    }
    return merge(left, right)
}
func merge(nums1, nums2 []int) []int {
    res := make([]int, len(nums1)+len(nums2))
    idx1, idx2 := 0, 0
    for i := range res {
        // nums1 遍历结束
        // nums2剩下直接入集
        if idx1 == len(nums1) { 
            res[i] = nums2[idx2] 
            idx2++
        } else if idx2 == len(nums2) { 
            // nums2 遍历结束
            // nums1剩下直接入集
            res[i] = nums1[idx1] 
            idx1++
        } else if nums1[idx1] <= nums2[idx2] {
            // 注意写成 <= 保持稳定性(相同元素原来靠前的，以后依然靠前)
            res[i] = nums1[idx1]
            idx1++
        } else {
            res[i] = nums2[idx2]
            idx2++
        }
    }
    return res
}
func insertSort(nums []int) []int {
    for i := 1; i < len(nums); i++ {
        temp := nums[i]
        j := i
        for ; j > 0 && nums[j-1] > temp; j-- {
            nums[j] = nums[j-1]
        }
        nums[j] = temp
    }
    return nums
}

归并+插入（无返回值）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

func sortArray(nums []int) []int {
    mergeSort(nums, 0, len(nums))
    return nums
}
func mergeSort(record []int, left, right int) {
    if right-left <= 7 {
        insertSort(record[left:right])
        return
    }
    // 防止两个大整数溢出
    mid := left + (right-left)/2 
    mergeSort(record, left, mid)
    mergeSort(record, mid, right)
    if record[mid-1] <= record[mid] {
        return
    }
    merge(record, left, mid, right)
}
func insertSort(arr []int) {
    for i := 1; i < len(arr); i++ {
        temp := arr[i]
        j := i
        for ; j > 0 && arr[j-1] > temp; j-- {
            arr[j] = arr[j-1]
        }
        arr[j] = temp
    }
}
func merge(record []int, left, mid, right int) {
    temp := make([]int, right-left)
    copy(temp, record[left:right])
    //tempMid/tempRight：表示左/右半部分子数组的长度，用于在合并过程中控制左/右半部分子数组的遍历
    tempMid, tempRight := mid-left, right-left
    idx1, idx2 := 0, tempMid
    for i := left; i < right; i++ {
        if idx1 == tempMid {
            record[i] = temp[idx2]
            idx2++
        } else if idx2 == tempRight {
            record[i] = temp[idx1]
            idx1++
        } else if temp[idx1] <= temp[idx2] {
            record[i] = temp[idx1]
            idx1++
        } else {
            record[i] = temp[idx2]
            idx2++
        }
    }
}

注意：实现归并排序的时候，要特别注意，要把这个算法实现成稳定排序，区别就在 <= 和 < ，已在代码中注明。

「归并排序」比「快速排序」好的一点是，它借助了额外空间，可以实现「稳定排序」，Java 里对于「对象数组」的排序任务，就是使用归并排序（的升级版 TimSort，在这里就不多做介绍）。

复杂度分析：

  • 时间复杂度：O(Nlog⁡N)O(Nlog⁡N)，这里 NN 是数组的长度；归并排序需要进行 logn 次拆分操作，合并操作的时间复杂度是 O(n)O(n)
  • 空间复杂度：O(N)O(N)，辅助数组与输入数组规模相当。
  • 稳定

「归并排序」也有「原地归并排序」和「不使用递归」的，但是不常用，其编码、调试都有一定难度。递归、分治处理问题的思想在基础算法领域是非常常见的，多练习「归并排序」学习递归思想，了解递归的细节，熟悉分治的思想。

经典问题：

交易逆序对的总数

LCR 170. 交易逆序对的总数

JZ51 数组中的逆序对_牛客题霸_牛客网

给定一个数组，假设当前元素大于后面某个元素，则这两个元素构成一个“逆序对”，求该数组中逆序对的个数

直观来看，使用暴力统计法即可，即遍历数组的所有数字对并统计逆序对数量。此方法时间复杂度为 O(N2)O(N^2)，观察题目给定的数组长度范围 0≤N≤5000000≤N≤500000，可知此复杂度是不能接受的。

「归并排序」与「逆序对」是息息相关的。合并阶段本质上是合并两个排序数组的过程，而每当遇到 左子数组当前元素 > 右子数组当前元素 时，意味着「左子数组当前元素 至 末尾元素」与「右子数组当前元素」构成了若干「逆序对」

注意：

  1. 不能用小数组插入排序，防止直接返回，没有归并过程，导致无法通过归并计数逆序对
  2. 计算res时，要用中间索引-当前索引，即[idx1, mid]，累加的是nums1当前元素后面的元素个数；不能用当前idx1 + 1，即[left, idx1]，这累加的是nums1当前元素前面的元素个数
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

var res int

func reversePairs(record []int) int {
    res = 0
    mergeSort(record, 0, len(record))
    return res
}
func mergeSort(record []int, left, right int) {
    if right-left <= 1 {
        return
    }
    // 防止两个大整数溢出
    mid := left + (right-left)/2 
    mergeSort(record, left, mid)
    mergeSort(record, mid, right)
    if record[mid-1] <= record[mid] {
        return
    }
    merge(record, left, mid, right)
}
func merge(record []int, left, mid, right int) {
    temp := make([]int, right-left)
    copy(temp, record[left:right])
    tempMid, tempRight := mid-left, right-left
    idx1, idx2 := 0, tempMid
    for i := left; i < right; i++ {
        if idx1 == tempMid {
            record[i] = temp[idx2]
            idx2++
        } else if idx2 == tempRight {
            record[i] = temp[idx1]
            idx1++
        } else if temp[idx1] <= temp[idx2] {
            record[i] = temp[idx1]
            idx1++
        } else {
            record[i] = temp[idx2]
            res += tempMid - idx1
            idx2++
        }
    }
}
// 写法二 无tempMid、tempRight
func reversePairs(record []int) int {
    res := 0
    var mergeSort func(int, int)
    mergeSort = func(left, right int) {
        if right-left <= 1 {
            return
        }
        mid := left + (right-left)>>1
        mergeSort(left, mid)
        mergeSort(mid, right)
        if record[mid-1] <= record[mid] {
            return
        }
        // 归并
        temp := make([]int, right-left)
        copy(temp, record[left:right])
        idx1, idx2 := 0, len(temp)>>1
        for i := left; i < right; i++ {
            if idx1 == len(temp)>>1 {
                record[i] = temp[idx2]
                idx2++
            } else if idx2 == len(temp) || temp[idx1] <= temp[idx2] {
                record[i] = temp[idx1]
                idx1++
            } else {
                record[i] = temp[idx2]
                idx2++
                res += len(temp)>>1-idx1
            }
        }
    }
    mergeSort(0, len(record))
    return res
}

  • 时间复杂度 O(Nlog⁡N)O(Nlog⁡N)：其中 NN 为数组长度；归并排序使用O(Nlog⁡N)O(Nlog⁡N)时间

  • 空间复杂度 O(N)O(N)：辅助数组占用 O(N)O(N)大小的额外空间

计算右侧小于当前元素的个数

315. 计算右侧小于当前元素的个数 - 力扣（LeetCode）

给定一个数组，要求返回一个数组，返回数组中每个位置的元素值，代表给定数组中对应位置元素值右边比它小的元素个数

和求逆序对类似，在合并时，每当左指针移动时，说明右区间首到当前右指针的前一个元素都小于当前左指针指向元素，在结果集中记录该元素数

注意：

  1. 在「并」的过程中 原数组中元素 的位置也一直在发生改变，所以引入一个新的容器，来记录旧数组下标，归并时跟随数组改变
  2. 由于有重复元素，所以不能用字典，只能用数组；
  3. 当原数组中元素变化时，对应下标数组也变化，排序的时候原数组和下标数组同时变化
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

var res []int
var idx []int

func countSmaller(nums []int) []int {
    res, idx = make([]int, len(nums)), make([]int, len(nums))
    for i := range nums {
        // 记录原数组下标
        idx[i] = i 
    }
    mergeSort(nums, 0, len(nums))
    return res
}
func mergeSort(nums []int, left, right int) {
    if right-left <= 1 {
        return
    }
    mid := left + (right-left)/2
    mergeSort(nums, left, mid)
    mergeSort(nums, mid, right)
    if nums[mid-1] <= nums[mid] {
        return
    }
    merge(nums, left, mid, right)
}
func merge(nums []int, left, mid, right int) {
    temp, tempIdx := make([]int, right-left), make([]int, right-left)
    copy(temp, nums[left:right])
    copy(tempIdx, idx[left:right])
    tempMid, tempRight := mid-left, right-left
    idx1, idx2 := 0, tempMid
    for i := left; i < right; i++ {
        if idx1 == tempMid {
            nums[i] = temp[idx2]
            idx[i] = tempIdx[idx2]
            idx2++
        } else if idx2 == tempRight {
            nums[i] = temp[idx1]
            idx[i] = tempIdx[idx1]
            res[idx[i]] += idx2 - tempMid
            idx1++
        } else if temp[idx1] <= temp[idx2] {
            nums[i] = temp[idx1]
            idx[i] = tempIdx[idx1]
            res[idx[i]] += idx2 - tempMid
            idx1++
        } else {
            nums[i] = temp[idx2]
            idx[i] = tempIdx[idx2]
            idx2++
        }
    }
}
  • 时间复杂度：O(nlog⁡n)O(nlog⁡n)，即归并排序的时间复杂度
  • 空间复杂度：O(n)O(n)，这里归并排序的临时数组、下标映射数组以及答案数组的空间代价均为 O(n)O(n)

翻转对

493. 翻转对 - 力扣（LeetCode）

给定一个数组 nums ，如果 i < j 且 nums[i] > 2*nums[j] 就将 (i, j) 称作一个*重要翻转对*。返回给定数组中的重要翻转对的数量。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

var res int

func reversePairs(nums []int) int {
	res = 0
	mergeSort(nums, 0, len(nums))
	return res
}

func mergeSort(nums []int, left, right int) {
	if right-left <= 1 {
		return
	}
	mid := left + (right-left)/2
	mergeSort(nums, left, mid)
	mergeSort(nums, mid, right)

	// 在合并前统计满足 nums[i] > 2 * nums[j] 的情况
	j := mid
	for i := left; i < mid; i++ {
		for j < right && nums[i] > 2*nums[j] {
			j++
		}
		res += j - mid
	}

	merge(nums, left, mid, right)
}

func merge(nums []int, left, mid, right int) {
	temp := make([]int, right-left)
	copy(temp, nums[left:right])

	idx1, idx2 := 0, mid-left
	for i := left; i < right; i++ {
		if idx1 == mid-left {
			nums[i] = temp[idx2]
			idx2++
		} else if idx2 == right-left {
			nums[i] = temp[idx1]
			idx1++
		} else if temp[idx1] <= temp[idx2] {
			nums[i] = temp[idx1]
			idx1++
		} else {
			nums[i] = temp[idx2]
			idx2++
		}
	}
}

快速排序🌟

重点

  • 基本思路：快速排序每一次都排定一个元素（这个元素待在了它最终应该待的位置），然后递归地去排它左边的部分和右边的部分，依次进行下去，直到数组有序；

  • 算法思想：分而治之（分治思想），与「归并排序」不同，「快速排序」在「分」这件事情上不像「归并排序」无脑地一分为二，而是采用了划分（partition）的方法，因此就没有「合」的过程

  • 实现细节（注意事项）：（针对特殊测试用例：顺序数组或者逆序数组）一定要随机化选择切分元素（pivot），否则在输入数组是有序数组或者是逆序数组的时候，快速排序会变得非常慢（等同于「冒泡排序」或者「选择排序」）；如果选择的基准值恰好是数组中的最大或最小元素，或者接近最大或最小元素，那么划分的结果将会非常不均衡，导致算法的时间复杂度退化到O(n2)O(n^2)，这种情况被称为最坏情况

排序过程：判断给定区间长度是否≥2，若不是则说明无元素或只有一个元素无需排序，若是则进入划分函数，随机选择一个值作为基准值交换到首元素，分割点初始化为首元素；从第二个元素开始遍历，每当遍历元素小于基准值，分割点前进一个单位，再将分割点值与当前遍历元素交换；遍历结束后，比基准值小的元素都会被交换到[1，分割点]，分割点右边元素都≥基准值，最后再将基准值与分割点交换，此时基准值左边元素都＜它，右边元素都≥它，返回分割点；分割点这个元素已经待在了它最终应该待的位置；继续向分割点左递归，向分割点右递归，对其左右子区间继续划分

排序过程优化：元素数≤7时用插入排序

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

func sortArray(nums []int) []int {
    // 使用当前时间作为随机种子
    rand.Seed(time.Now().UnixNano()) 
    quickSort(nums, 0, len(nums))
    return nums
}
func quickSort(nums []int, left, right int) {
    if left < right {
        pivot := partition(nums, left, right)
        quickSort(nums, left, pivot)
        quickSort(nums, pivot+1, right)
    }
}
func partition(nums []int, left, right int) int {
    // 随机选择基准值的索引
    randomIndex := rand.Intn(right-left) + left 
    nums[left], nums[randomIndex] = nums[randomIndex], nums[left]
    // 分割点
    idx := left 
    for i := left + 1; i < right; i++ {
        if nums[i] < nums[left] {
            idx++
            nums[idx], nums[i] = nums[i], nums[idx]
        }
    }
    nums[idx], nums[left] = nums[left], nums[idx]
    return idx
}
  • 时间复杂度：O(Nlog⁡N)O(Nlog⁡N)，这里 NN 是数组的长度
  • 空间复杂度：O(log⁡N)O(log⁡N)，这里占用的空间主要来自递归函数的栈空间

快速排序丢失了稳定性，如果需要稳定的快速排序，需要具体定义比较函数，这个过程叫「稳定化」，在这里就不展开了

使用「快速排序」解决的经典问题（非常重要）：

数组中的第K个最大元素

215. 数组中的第K个最大元素 - 力扣（LeetCode）

给定一个数组和整数k，返回数组中第k个最大的元素

快速排序的核心包括“哨兵划分” 和 “递归” 。

  • 哨兵划分： 以数组某个元素（一般选取首元素）为基准数，将所有小于基准数的元素移动至其左边，大于基准数的元素移动至其右边。

  • 递归： 对 左子数组 和 右子数组 递归执行 哨兵划分，直至子数组长度为 1 时终止递归，即可完成对整个数组的排序。

「快速选择」：设 NN 为数组长度。根据快速排序原理，如果某次哨兵划分后，基准数的索引正好是 N−kN−k ，则意味着它就是第 kk 大的数字 。此时就可以直接返回它，无需继续递归下去了。

然而，对于包含大量重复元素的数组，每轮的哨兵划分都可能将数组划分为长度为 11 和 n−1n−1 的两个部分，这种情况下快速排序的时间复杂度会退化至 O(N2)O(N^2)

一种解决方案是使用「三路划分」，即每轮将数组划分为三个部分：小于、等于和大于基准数的所有元素。这样当发现第 kk 大数字处在“等于基准数”的子数组中时，便可以直接返回该元素。

为了进一步提升算法的稳健性，我们采用随机选择的方式来选定基准数。

  • k <= len(big)：比基准大的都有len(big)个元素，要求第k大，若k <= len(big)，则第k大一定在big中
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

func findKthLargest(nums []int, k int) int {
    // 使用当前时间作为随机种子
    rand.Seed(time.Now().UnixNano()) 
    return quickSelect(nums, k)
}
func quickSelect(nums []int, k int) int {
    // 随机选择基准值的索引
    randomIndex := rand.Intn(len(nums)) 
    pivot := nums[randomIndex]
    big, equal, small := make([]int, 0), make([]int, 0), make([]int, 0)
    for i := range nums {
        if nums[i] > pivot {
            big = append(big, nums[i])
        } else if nums[i] < pivot {
            small = append(small, nums[i])
        } else {
            equal = append(equal, nums[i])
        }
    }
    // 第k大一定在big中
    if k <= len(big) { 
        return quickSelect(big, k)
    }
    // 第k大一定在small中
    if k > len(big)+len(equal) { 
        return quickSelect(small, k-(len(big)+len(equal)))
    }
    // 第k大在equal中，直接返回pivot
    return pivot 
}

  • 时间复杂度 O(N)O(N) ： 其中 NN 为数组元素数量。

  • 空间复杂度 O(log⁡N)O(log⁡N) ： 划分函数的平均递归深度为 O(log⁡N)O(log⁡N)

颜色分类

75. 颜色分类 - 力扣（LeetCode）

给定一个数组包含0、1、2三种元素，原地排序，时间复杂度最好为O(N)O(N)

本题考察的是「快速排序」的子过程 partition，即：通过一次遍历，把数组分成三个部分

  • [0, zero) = 0
  • [zero, i) = 1
  • [two, len - 1] = 2

注意：因为只有在遇到0或1的时候i才会++，所以可以保证i之前的一定是0或1；在遇到1时，只有i++，这保证了[zero, i)一定是1；在遇到2时，换到i的有可能还是2，所以不能让i++，需要再检查一下

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

func sortColors(nums []int) {
	zero, i, two := 0, 0, len(nums)
	for i < two {
		if nums[i] == 0 {
			nums[zero], nums[i] = nums[i], nums[zero]
			zero++
			i++
		} else if nums[i] == 1 {
			i++
		} else {
			two--
			nums[two], nums[i] = nums[i], nums[two]
		}
	}
}
  • 时间复杂度：O(N)O(N)，这里 NN 是输入数组的长度
  • 空间复杂度：O(1)O(1)

堆排序🌟

堆很重要，堆排序根据个人情况掌握

堆排序是选择排序的优化，选择排序需要在未排定的部分里通过「打擂台」的方式选出最大的元素（复杂度 O(N)O(N)），而「堆排序」就把未排定的部分构建成一个「堆」，这样就能以 O(log⁡N)O(log⁡N) 的方式选出最大元素；

堆是一种相当有意思的数据结构，它在很多语言里也被命名为「优先队列」。它是建立在数组上的「树」结构，类似的数据结构还有「并查集」「线段树」等。 「优先队列」是一种特殊的队列，按照优先级顺序出队，从这一点上说，与「普通队列」无差别。「优先队列」可以用数组实现，也可以用有序数组实现，但只要是线性结构，复杂度就会高，因此，「树」结构就有优势，「优先队列」的最好实现就是「堆」。

堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。 如果是父结点大于等于左右孩子那就是大顶堆，小于等于左右孩子就是小顶堆。大顶堆（堆头是最大元素），小顶堆（堆头是最小元素）

由于堆是一棵完全二叉树，所以可以用数组来存储，只需要通过简单的代数表达式，就能计算出要某个节点的父节点和子节点的索引位置，既避免了像链表那样使用指针来保持结构，又能高效的执行相应操作。

关于节点的父节点和子节点在堆中的位置需要记住下面三个公式：

  • 节点 i 的左子节点为2 * i + 1，右子节点为 2 * i + 2
  • 节点 i 的父节点为 (i - 1) / 2

排序过程：

  1. 构建大顶堆： 这个步骤是堆排序算法的第一步。在构建大顶堆时，从数组的中间位置开始，向前遍历到第一个元素，对每个非叶子节点进行堆化操作，将当前节点与其子节点进行比较，并确保以当前节点为根的子树满足大顶堆的性质。这一步骤的目的是将整个数组转换为一个大顶堆结构，以便进行后续的排序操作。
  2. 堆排序： 这个步骤是堆排序算法的第二步。在构建好大顶堆后，重复执行以下操作直到整个数组排序完成：首先，将当前堆顶元素（即最大值）与数组末尾元素交换，然后缩小堆的范围并重新调整剩余元素，使其仍然满足大顶堆的性质。通过重复这个过程，最终得到一个有序的数组。

为什么构建完大顶堆后数组还不是有序的？

  • 构建完大顶堆后并不意味着数组已经有序，因为大顶堆仅保证了每个节点都比其子节点大，但并没有保证整个数组是有序的（堆内局部有序，整体不一定有序）。在大顶堆中，堆顶元素是最大的，但堆中其他节点的相对位置并不一定符合排序顺序。
  • 堆排序算法的关键在于构建好大顶堆后，通过反复将堆顶元素（最大值）交换到数组末尾，并重新调整剩余元素，使得剩余部分仍然构成一个大顶堆，从而逐步完成排序过程。通过这种方式，剩余部分的最大值会被依次放置在数组的末尾，直到整个数组有序。

因此，在堆排序算法中，构建大顶堆只是第一步，而真正实现排序的过程是通过不断将堆顶元素弹出并进行调整，直到整个数组有序为止。

更深理解

  • 堆是一种数据结构，排序是利用该数据结构的堆顶一定最大/小的性质，每次堆顶交换到堆尾都排定一个元素
  • 求升序，用大顶堆；求降序，用小顶堆
  • 排序会破坏堆结构，排序后就不是堆了
  • 排序从尾节点开始遍历到根，每次排定一个元素，再对剩余元素重新堆化，使顶为最值，下次再交换到未排定尾，直达所有元素排定
  • 若是给定一个数组，要将其堆化，则直接从尾节点的父节点向前遍历，每次遍历时，若发生交换则向下递归调整子树
  • 若是向一个堆中添加元素，则将其添加到尾，从尾向上与父节点比较，若发生交换则继续向上递归交换；若是从一个堆中删除元素，则将其与尾交换后删除尾，最后比较当前位置与父亲，若小/大于父亲（小/大顶堆），则向上递归交换；否则向下与子节点比较交换
  • 尾节点的父节点：(i-1) / 2 = (len(nums)-1-1) / 2 = len(nums)/2 - 1
  • 涉及不断添加和删除更新堆时，不能每次更新后都重新自底向上构建堆，效率较低；建议用 up 和 down等操作减少不必要的 heapify 调用，减少冗余堆重构的开销
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

func sortArray(nums []int) []int {
    // 构建大顶堆(从尾节点的父节点向上遍历到根节点)
    for i := len(nums)/2 - 1; i >= 0; i-- {
        heapify(nums, len(nums), i)
    }
    // 堆排序
    for i := len(nums) - 1; i >= 0; i-- {
        // 将当前最大的元素 nums[0] 交换到数组末尾
        nums[0], nums[i] = nums[i], nums[0]
        // 将剩余元素重新调整为大顶堆
        heapify(nums, i, 0)
    }
    return nums
}

// 堆化函数，将以 i 为根的子树调整为大顶堆
func heapify(nums []int, len, i int) {
    largest := i
    left := 2*i + 1
    right := 2*i + 2

    // 如果左子节点存在且大于根节点，则更新最大值索引为左子节点
    if left < len && nums[left] > nums[largest] {
        largest = left
    }

    // 如果右子节点存在且大于根节点或者左子节点，则更新最大值索引为右子节点
    if right < len && nums[right] > nums[largest] {
        largest = right
    }

    // 如果最大值索引不是当前根节点，则交换根节点和最大值节点，并向下递归调整被交换节点的子树
    if largest != i {
        nums[i], nums[largest] = nums[largest], nums[i]
        heapify(nums, len, largest)
    }
}
  • 时间复杂度：O(Nlog⁡N)O(Nlog⁡N)，这里 NN 是数组的长度；建堆的时间代价是 O(n)，堆排序的时间代价为O(Nlog⁡N)O(Nlog⁡N)
    • 调整次数并不是均匀分布的，而是随着层级的上升而减少
    • 堆排序相当于执行n-1次O(logn)
  • 空间复杂度：O(1)O(1)，若考虑递归使用栈空间的空间代价，则为O(log⁡N)O(log⁡N)

手写完整大顶堆

  • 增删元素时用h *Heap：其中访问元素时用(*h)[i]，调用方法时用h.Swap()，增删时用*h = append(*h, i)、*h = (*h)[:len(*h)-1]
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

type Heap []int

// 交换两个节点的值
func (h Heap) swap(i, j int) {
    h[i], h[j] = h[j], h[i]
}

// 比较两个节点的值
func (h Heap) less(i, j int) bool {
    // 如果实现的是小顶堆，修改这里的判断即可
    return h[i] > h[j]
}

func (h Heap) up(i int) {
    father := (i - 1) / 2
    if father >= 0 && h.less(i, father) {
        h.swap(father, i)
        h.up(father)
    }
}

func (h Heap) down(i int) {
    largest := i
    left := 2*i + 1
    right := 2*i + 2
    if left < len(h) && h.less(left, largest) {
        largest = left
    }
    if right < len(h) && h.less(right, largest) {
        largest = right
    }
    if largest != i {
        h.swap(largest, i)
        h.down(largest)
    }
}

// 注意go中所有参数都是值传递
// 所以要让h的变化在函数外也起作用，此处要传指针
func (h *Heap) Push(x int) {
    *h = append(*h, x)
    h.up(len(*h) - 1)
}

// 删除堆中位置为i的元素
// 返回被删元素的值
func (h *Heap) Remove(i int) (int, bool) {
    if i < 0 || i > len(*h)-1 {
        return 0, false
    }
    // 交换要删除的元素与尾元素
    h.swap(i, len(*h)-1)
    // 删除最后的元素
    x := (*h)[len(*h)-1]
    *h = (*h)[:len(*h)-1]
    // 若最初要删除元素非尾元素，则调整堆
    if i < len(*h) {
        father := (i - 1) / 2
        // 若当前元素大于父节点，向上交换递归
        if father >= 0 && h.less(i, father) {
            h.up(i)
        } else {
            // 当前元素小于父节点，向下比较交换递归
            h.down(i)
        }
    }
    return x, true
}

// 弹出堆顶的元素，并返回其值
func (h *Heap) Pop() int {
    x, _ := h.Remove(0)
    return x
}

Go标准库的堆

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

import (
    "container/heap"
)
func main() {
    h := Heap{}
    // 取出元素是any需要手动按照堆元素类型转换
    // 接口的 Push 和 Pop 方法是供 heap 包调用的，用 heap.Push 和 heap.Pop 来向一个堆添加或者删除元素
    p := heap.Pop(&h.(int))
    var v int
    v = 1
    heap.Push(&h, v)
}

type Heap []int // 可以自定义堆元素类型

func (h Heap) Len() int           { return len(h) }
func (h Heap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }
func (h Heap) Less(i, j int) bool { return h[i] < h[j] } // 大顶堆的话修改此处
func (h *Heap) Push(v any)        { *h = append(*h, v.(int)) }
func (h *Heap) Pop() any          { x := (*h)[len(*h)-1]; *h = (*h)[:len(*h)-1]; return x }

相关题

数组中的第K个最大元素

215. 数组中的第K个最大元素 - 力扣（LeetCode）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

type Heap []int

func findKthLargest(nums []int, k int) int {
    // 维护一个大小为k的最小堆
    heap := Heap{}
    for _, v := range nums {
        if len(heap) < k {
            heap.Push(v)
        } else if v > heap[0] {
            heap.Pop()
            heap.Push(v)
        }
    }
    return heap[0]
}

func (h Heap) swap(i, j int) {
    h[i], h[j] = h[j], h[i]
}

func (h Heap) less(i, j int) bool {
    return h[i] < h[j]
}

func (h Heap) up(i int) {
    father := (i - 1) / 2
    if father >= 0 && h.less(i, father) {
        h.swap(i, father)
        h.up(father)
    }
}

func (h Heap) down(i int) {
    smallest := i
    left := i*2 + 1
    right := i*2 + 2
    if left < len(h) && h.less(left, smallest) {
        smallest = left
    }
    if right < len(h) && h.less(right, smallest) {
        smallest = right
    }
    if smallest != i {
        h.swap(smallest, i)
        h.down(smallest)
    }
}

func (h *Heap) Push(val int) {
    (*h) = append((*h), val)
    h.up(len(*h) - 1)
}

func (h *Heap) Remove(i int) (int, bool) {
    if i < 0 || i >= len(*h) {
        return -1, false
    }
    x := (*h)[i]
    h.swap(i, len(*h)-1)
    (*h) = (*h)[:len(*h)-1]
    if i != len(*h) {
        h.down(i)
    }
    return x, true
}

func (h *Heap) Pop() int {
    x, _ := h.Remove(0)
    return x
}

  • 时间复杂度：O(nlogn)，建堆的时间代价是 O(n)，删除的总代价是 O(klogn)，因为 k<n，故渐进时间复杂为 O(n+klogn)=O(nlogn)

  • 空间复杂度：O(logn)，即递归使用栈空间的空间代价

查找和最小的 K 对数字

373. 查找和最小的 K 对数字 - 力扣（LeetCode）

给定两个升序数组 nums1 和 nums2 , 以及一个整数 k 。定义一对值 (u,v)，其中第一个元素来自 nums1，第二个元素来自 nums2 。找到和最小的 k 个数对 (u1,v1), (u2,v2) … (uk,vk) 返回

思路：小顶堆

假设i,j最小——>可能的次小i,j+1、i+1,j入堆——>有数对重复入堆——>规定只入堆i,j+1——>初始入堆0,0后i一直为0不变——>初始入堆各个i,0

为描述方便，下文把nums1记作a，nums2记作b。

由于数组是有序的，(a[0],b[0])是和最小的数对，计入答案。次小的只能是 (a[0],b[1]) 或 (a[1],b[0])。

为了更高效地比大小，借助最小堆来优化：堆中保存下标(i, j)，堆顶是最小的 a[i]+b[j]。初始把 (0,0) 入堆。每次出堆时，可能成为次小数对的(i+1,j) 和 (i,j+1)入堆。

但这会导致一个问题：例如当 (1,0) 出堆时，会把 (1,1) 入堆；当 (0,1) 出堆时，也会把 (1,1) 入堆，这样堆中会有重复元素。为了避免有重复元素，规定 (i,j−1) 出堆时，将 (i,j) 入堆；而 (i−1,j) 出堆时只计入答案，其它什么也不做。

换句话说，在 (i,j) 出堆时，只需将 (i,j+1) 入堆，无需将 (i+1,j) 入堆。

但若按照该规则，初始仅把 (0,0) 入堆的话，只会得到 (0,1),(0,2),⋯这些下标对。

所以初始不仅要把 (0,0) 入堆，(1,0),(2,0),⋯ (min(k, n), 0) 这些都要入堆。

注意：

  • 堆的初始长度设为 min(k, n)，保证当k<n时，只初始化k个数对，当n<k时，只能初始化n个数对
  • 代码实现时，为了方便比较大小，实际入堆的是三元组 (i, j, a[i]+b[j])
  • 也可以在循环的过程中去把 (i+1,0) 入堆。由于一开始堆的大小不大，出堆入堆更快，整体效率更高。

写法一：自实现小顶堆

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84

type Heap [][]int

func kSmallestPairs(nums1 []int, nums2 []int, k int) [][]int {
    // 初始化一个大小为min(k, n)的小顶堆
    heap := make(Heap, min(k, len(nums1)))
    // 初始化加入(0,0,v)(1,0,v)...(min(k, n),0,v)
    for i := range heap {
        heap[i] = []int{i, 0, nums1[i] + nums2[0]}
    }
    // 维护小顶堆(取堆顶最小->可能的次小入堆)k次
    res := [][]int{}
    for cnt := 0; cnt < k; cnt++ {
        // 取堆顶(i, j)
        i, j := heap[0][0], heap[0][1]
        // (a[i], b[j])加入结果集
        res = append(res, []int{nums1[i], nums2[j]})
        heap.Pop()
        // 加入(i, j+1)
        // 防止越界
        if j+1 < len(nums2) {
            heap.Push(i, j+1, nums1[i]+nums2[j+1])
        }
    }
    return res
}
func (h Heap) swap(i, j int) {
    h[i], h[j] = h[j], h[i]
}

func (h Heap) less(i, j int) bool {
    return h[i][2] < h[j][2]
}

func (h Heap) up(i int) {
    father := (i - 1) / 2
    if father >= 0 && h.less(i, father) {
        h.swap(father, i)
        h.up(father)
    }
}

func (h Heap) down(i int) {
    largest := i
    left := 2*i + 1
    right := 2*i + 2
    if left < len(h) && h.less(left, largest) {
        largest = left
    }
    if right < len(h) && h.less(right, largest) {
        largest = right
    }
    if largest != i {
        h.swap(largest, i)
        h.down(largest)
    }
}

func (h *Heap) Push(i, j, v int) {
    *h = append(*h, []int{i, j, v})
    h.up(len(*h) - 1)
}

func (h *Heap) Remove(i int) ([]int, bool) {
    if i < 0 || i >= len((*h)) {
        return []int{}, false
    }
    h.swap(i, len(*h)-1)
    x := (*h)[len(*h)-1]
    *h = (*h)[:len(*h)-1]
    if i < len(*h) {
        father := (i - 1) / 2
        if father >= 0 && h.less(i, father) {
            h.up(i)
        } else {
            h.down(i)
        }
    }
    return x, true
}

func (h *Heap) Pop() []int {
    x, _ := h.Remove(0)
    return x
}

写法二：自实现小顶堆 循环中加入(i+1, 0)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84

type Heap [][]int

func kSmallestPairs(nums1 []int, nums2 []int, k int) [][]int {
    // 初始化小顶堆加入(0,0,v)
    heap := Heap{[]int{0, 0, nums1[0] + nums2[0]}}
    // 维护小顶堆(取堆顶最小->可能的次小入堆)k次
    res := make([][]int, 0, k)
    for cnt := 0; cnt < k; cnt++ {
        // 取堆顶(i, j)
        i, j := heap[0][0], heap[0][1]
        // (a[i], b[j])加入结果集
        res = append(res, []int{nums1[i], nums2[j]})
        heap.Pop()
        // 当j=0时,加入(i+1, 0)
        if j == 0 && i+1 < len(nums1) {
            heap.Push(i+1, 0, nums1[i+1]+nums2[0])
        }
        // 加入(i, j+1)
        // 防止越界
        if j+1 < len(nums2) {
            heap.Push(i, j+1, nums1[i]+nums2[j+1])
        }
    }
    return res
}
func (h Heap) swap(i, j int) {
    h[i], h[j] = h[j], h[i]
}

func (h Heap) less(i, j int) bool {
    return h[i][2] < h[j][2]
}

func (h Heap) up(i int) {
    father := (i - 1) / 2
    if father >= 0 && h.less(i, father) {
        h.swap(father, i)
        h.up(father)
    }
}

func (h Heap) down(i int) {
    largest := i
    left := 2*i + 1
    right := 2*i + 2
    if left < len(h) && h.less(left, largest) {
        largest = left
    }
    if right < len(h) && h.less(right, largest) {
        largest = right
    }
    if largest != i {
        h.swap(largest, i)
        h.down(largest)
    }
}

func (h *Heap) Push(i, j, v int) {
    *h = append(*h, []int{i, j, v})
    h.up(len(*h) - 1)
}

func (h *Heap) Remove(i int) ([]int, bool) {
    if i < 0 || i >= len((*h)) {
        return []int{}, false
    }
    h.swap(i, len(*h)-1)
    x := (*h)[len(*h)-1]
    *h = (*h)[:len(*h)-1]
    if i < len(*h) {
        father := (i - 1) / 2
        if father >= 0 && h.less(i, father) {
            h.up(i)
        } else {
            h.down(i)
        }
    }
    return x, true
}

func (h *Heap) Pop() []int {
    x, _ := h.Remove(0)
    return x
}

写法三：标准库

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

func kSmallestPairs(nums1 []int, nums2 []int, k int) [][]int {
    // 初始化小顶堆加入(0,0,v)
    h := Heap{[]int{0, 0, nums1[0] + nums2[0]}}
    // 维护小顶堆(取堆顶最小->可能的次小入堆)k次
    res := make([][]int, 0, k)
    for cnt := 0; cnt < k; cnt++ {
        // 取堆顶(i, j)
        p := heap.Pop(&h).([]int)
        i, j := p[0], p[1]
        // (a[i], b[j])加入结果集
        res = append(res, []int{nums1[i], nums2[j]})
        // 当j=0时,加入(i+1, 0)
        if j == 0 && i+1 < len(nums1) {
            heap.Push(&h, []int{i + 1, 0, nums1[i+1] + nums2[0]})
        }
        // 加入(i, j+1)
        // 防止越界
        if j+1 < len(nums2) {
            heap.Push(&h, []int{i, j + 1, nums1[i] + nums2[j+1]})
        }
    }
    return res
}

type Heap [][]int

func (h Heap) Len() int           { return len(h) }
func (h Heap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }
func (h Heap) Less(i, j int) bool { return h[i][2] < h[j][2] }
func (h *Heap) Push(v any)        { *h = append(*h, v.([]int)) }
func (h *Heap) Pop() any          { x := (*h)[len(*h)-1]; *h = (*h)[:len(*h)-1]; return x }
  • 时间复杂度：O(klogmin(n,k))，其中 n 为 nums1的长度。为了得到 k 个数对，需要循环 k 次，每次出堆入堆的时间复杂度为 logmin(n,k)。所以总的时间复杂度为 O(klogmin(n,k))。
  • 空间复杂度：O(min(n,k))。堆中至多有 O(min(n,k)) 个三元组。

丑数 II

264. 丑数 II - 力扣（LeetCode）

给一个整数 n ，找出并返回第 n 个 丑数 。丑数 就是质因子只包含 2、3 和 5 的正整数

思路一：小顶堆+哈希表去重

根据题意，每个丑数都可以由其他较小的丑数通过乘以 2 或 3 或 5 得到。

所以，可以考虑使用一个优先队列保存所有的丑数，每次取出最小的那个，然后乘以 2 , 3 , 5 后放回队列。然而，这样做会出现重复的丑数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

type Heap []int

func nthUglyNumber(n int) int {
    // 初始化1入堆
    heap := Heap{1}
    // 哈希去重
    mp := map[int]bool{}
    // 不断循环直到取出第n个丑数
    for {
        // 取出当前堆中最小丑数
        curMin := heap.Pop()
        // 判是否取到第n个丑数
        n--
        if n == 0 {
            return curMin
        }
        // 得到三个候选丑数
        a, b, c := curMin*2, curMin*3, curMin*5
        // 去重后入堆
        if !mp[a] {
            heap.Push(a)
            mp[a] = true
        }
        if !mp[b] {
            heap.Push(b)
            mp[b] = true
        }
        if !mp[c] {
            heap.Push(c)
            mp[c] = true
        }
    }
}

  • 时间复杂度：O(nlogn)。得到第 n 个丑数需要进行 n 次循环，每次循环都要从最小堆中取出 1 个元素以及向最小堆中加入最多 3 个元素，因此每次循环的时间复杂度是 O(log(3n)+3log(3n))=O(logn)，总时间复杂度是 O(nlogn)

  • 空间复杂度：O(n)。空间复杂度主要取决于最小堆和哈希集合的大小，最小堆和哈希集合的大小都不会超过 3n

思路二：动态规划

思路一使用最小堆，会预先存储较多的丑数，维护最小堆的过程也导致时间复杂度较高。可以使用动态规划的方法进行优化。

  1. dp[i]：第i个丑数
  2. 递推公式：dp[i] = min(dp[a]*2, dp[b]*3, dp[c]*5)
  3. 初始化：dp[1] = 1

利用三个指针生成丑数的算法流程：

  1. 初始化丑数列表 dp ，首个丑数为 1 ，三个指针 a , b, c 都指向首个丑数

  2. 开启循环生成丑数：

    • 计算下一个丑数的候选集 dp[a]⋅2 , dp[b]⋅3 , dp[c]⋅5
    • 选择丑数候选集中最小的那个作为下一个丑数，填入 dp
    • 将被选中的丑数对应的指针向右移动一格

  3. 返回 dp 的最后一个元素即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

func nthUglyNumber(n int) int {
    dp := make([]int, n+1)
    dp[1] = 1
    a, b, c := 1, 1, 1
    for i := 2; i <= n; i++ {
        dp[i] = min(dp[a]*2, dp[b]*3, dp[c]*5)
        if dp[i] == dp[a]*2 {
            a++
        }
        if dp[i] == dp[b]*3 {
            b++
        }
        if dp[i] == dp[c]*5 {
            c++
        }
    }
    return dp[n]
}
  • 时间复杂度 O(n) ： 计算 dp 列表需遍历 n−1 轮
  • 空间复杂度 O(n) ： 长度为 n 的 dp 列表使用 O(n) 的额外空间

IPO

502. IPO - 力扣（LeetCode）

给定可启动的项目数k、初始资金k，各个项目的利润profits和需要的启动资金capital。计算最终可获得的最高利润

思路：维护一个根据项目利润构建的大顶堆k次，不断循环从剩余项目里取项目入堆直到不可启动，判堆空，取出堆顶最大利润的项目启动

注意：为了每次入堆时取的都是剩余项目里启动资金最小的，构造一个项目利润和启动资金关联的二元组，按照启动资金对其升序重排

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90

type project struct {
    profit int
    capital int
}

type Heap []int

func findMaximizedCapital(k int, w int, profits []int, capital []int) int {
    // 构造项目的利润与启动资金的二元组
    projects := make([]project, len(profits))
    for i := range profits {
        projects[i] = project{profits[i], capital[i]}
    }
    // 对项目按启动资金升序重排
    sort.Slice(projects, func(i, j int) bool {
        return projects[i].capital < projects[j].capital
    })
    idx := 0
    heap := Heap{}
    // 维护一个根据利润构建的大顶堆k次
    for i := 0; i < k ; i++ {
        // 不断入堆直至无法启动
        for idx < len(projects) && projects[idx].capital <= w {
            heap.Push(projects[idx].profit)
            idx++
        }
        // 判堆空
        if len(heap) == 0 {
            break
        }
        // 取堆顶
        w += heap.Pop()
    }
    return w
}

func (h Heap) swap(i, j int) {
    h[i], h[j] = h[j], h[i]
}

func (h Heap) less(i, j int) bool {
    return h[i] > h[j]
}

func (h Heap) up(i int) {
    father := (i-1)/2
    if father >= 0 && h.less(i, father) {
        h.swap(father, i)
        h.up(father)
    }
}

func (h Heap) down(i int) {
    left := i*2+1
    right := i*2+2
    largest := i
    if left < len(h) && h.less(left, largest) {
        largest = left
    }
    if right < len(h) && h.less(right, largest) {
        largest = right
    }
    if largest != i {
        h.swap(i, largest)
        h.down(largest)
    }
}

func (h *Heap) Push(x int) {
    *h = append(*h, x)
    h.up(len(*h)-1)
}

func (h *Heap) Remove(i int) (int, bool) {
    if i < 0 || i > len(*h)-1 {
        return -1, false
    }
    h.swap(i, len(*h)-1)
    x := (*h)[len(*h)-1]
    *h = (*h)[:len(*h)-1]
    if i != len(*h) {
        h.down(i)
    }
    return x, true
}

func (h *Heap) Pop() int {
    x, _ := h.Remove(0)
    return x
}

数据流的中位数

295. 数据流的中位数 - 力扣（LeetCode）

JZ41 数据流中的中位数_牛客题霸_牛客网

思路：维护一个大顶堆、一个小顶堆，中间值是大顶堆（奇）或（大顶堆顶+小顶堆顶）/ 2（偶）

使用两个优先队列（堆）来维护整个数据流数据，为了可以在 O(1) 的复杂度内取得当前中位数，令 l 为大根堆，r 为小根堆，并人为固定 l 和 r 之前存在如下关系：

  • 当数据流元素数量为偶数：l 和 r 大小相同，此时中位数为两者堆顶元素的平均值；
  • 当数据流元素数量为奇数：l 比 r 多一，此时中位数为 l 的堆顶原数

当添加一个数 num 时需要分情况讨论：

  1. num≤maxlnum≤max{l}

    此时 num 小于等于中位数，需要将该数添加到 l 中。新的中位数将小于等于原来的中位数，因此可能需要将 l 中最大的数移动到 r 中。

  2. num>maxrnum>max{r}

    此时 num 大于中位数，需要将该数添加到 r 中。新的中位数将大于等于原来的中位数，因此可能需要将 r 中最小的数移动到 l 中。

具体是否移动取决与俩堆的大小，目标是维持俩堆大小相等或左比右大1

特别地，当 l 为空时，将 num 添加到 l 中

注意：

  1. 大顶堆为空时，放大顶堆
  2. 每次入堆后判断两堆大小，大顶堆元素数和小顶堆元素数必须相差不超过1，若超过则移动
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109

type MedianFinder struct {
    heapL Heap // 大顶堆
    heapR Heap // 小顶堆
}

func Constructor() MedianFinder {
    return MedianFinder{
        heapL: Heap{},
        heapR: Heap{},
    }
}

func (this *MedianFinder) AddNum(num int) {
    // 判大顶堆是否为空或加入值小于大顶堆顶
    if len(this.heapL) == 0 || num < this.heapL[0] {
        // 加入大顶堆
        this.heapL.Push(num, 1)
        // 判大顶堆元素是否比小顶堆元素多一个以上
        if len(this.heapL)-len(this.heapR) > 1 {
            // 大顶堆顶移至小顶堆
            this.heapR.Push(this.heapL.Pop(1), 0)
        }
    } else {
        // 加入小顶堆
        this.heapR.Push(num, 0)
        // 判小顶堆元素是否多于大顶堆
        if len(this.heapR) > len(this.heapL) {
            // 小顶堆顶移至大顶堆
            this.heapL.Push(this.heapR.Pop(0), 1)
        }
    }
}

func (this *MedianFinder) FindMedian() float64 {
    // 判大顶堆元素是否多于小顶堆
    if len(this.heapL) > len(this.heapR) {
        return float64(this.heapL[0])
    } else {
        return float64(this.heapL[0]+this.heapR[0]) / 2.0
    }
}

type Heap []int

func (h Heap) swap(i, j int) {
    h[i], h[j] = h[j], h[i]
}

func (h Heap) less(i, j, sign int) bool {
    if sign == 0 {
        // 小顶堆
        return h[i] < h[j]
    } else {
        // 大顶堆
        return h[i] > h[j]
    }
}

func (h Heap) up(i, sign int) {
    father := (i - 1) / 2
    if father >= 0 && h.less(i, father, sign) {
        h.swap(father, i)
        h.up(father, sign)
    }
}

func (h Heap) down(i, sign int) {
    largest := i
    left := 2*i + 1
    right := 2*i + 2
    if left < len(h) && h.less(left, largest, sign) {
        largest = left
    }
    if right < len(h) && h.less(right, largest, sign) {
        largest = right
    }
    if largest != i {
        h.swap(largest, i)
        h.down(largest, sign)
    }
}

func (h *Heap) Push(x, sign int) {
    *h = append(*h, x)
    h.up(len(*h)-1, sign)
}

func (h *Heap) Remove(i, sign int) (int, bool) {
    if i < 0 || i >= len(*h) {
        return -1, false
    }
    h.swap(i, len(*h)-1)
    x := (*h)[len(*h)-1]
    *h = (*h)[:len(*h)-1]
    if i < len(*h) {
        father := (i - 1) / 2
        if father >= 0 && h.less(i, father, sign) {
            h.up(i, sign)
        } else {
            h.down(i, sign)
        }
    }
    return x, true
}

func (h *Heap) Pop(sign int) int {
    x, _ := h.Remove(0, sign)
    return x
}
  • 时间复杂度：
    • addNum: O(logn)，其中 n 为累计添加的数的数量
    • findMedian: O(1)。
  • 空间复杂度：O(n)，主要为堆的开销

无限集中的最小数字

2336. 无限集中的最小数字 - 力扣（LeetCode）

要求对一个无限集[1, +∞]实现增删操作

思路：由于是无限集，所以使用 idx 代表顺序弹出的集合左边界，[idx, +∞] 范围内的数均为待弹出，起始有 idx=1，考虑当调用addBack 往集合添加数值 x 时：

  • x ≥ idx：说明数值本身就存在于集合中，忽略该添加操作；
  • x == idx−1：数值刚好位于边界左侧，更新 idx=idx−1；
  • x < idx−1：考虑将数值添加到某个容器中，该容器支持返回最小值，容易联想到“小根堆”；但小根堆并没有“去重”功能，为防止重复弹出，还需额外使用“哈希表”来记录哪些元素在堆中

总结：堆中存idx之前不连续的值，弹出时先弹堆中的；idx记录连续值的开头，哈希表记录堆中不连续的值的存在情况

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114

// 写法一
type Heap []int
type SmallestInfiniteSet struct {
    heap Heap
    mp   map[int]bool
}

func Constructor() SmallestInfiniteSet {
    smallestInfiniteSet := SmallestInfiniteSet{}
    smallestInfiniteSet.mp = map[int]bool{}
    for i := 1; i <= 1000; i++ {
        smallestInfiniteSet.heap.Push(i)
        smallestInfiniteSet.mp[i] = true
    }
    return smallestInfiniteSet
}

func (this *SmallestInfiniteSet) PopSmallest() int {
    this.mp[this.heap[0]] = false
    return this.heap.Pop()
}

func (this *SmallestInfiniteSet) AddBack(num int) {
    if !this.mp[num] {
        this.heap.Push(num)
        this.mp[num] = true
    }
}

func (h Heap) swap(i, j int) {
    h[i], h[j] = h[j], h[i]
}
func (h Heap) less(i, j int) bool {
    return h[i] < h[j]
}
func (h Heap) up(i int) {
    father := (i - 1) / 2
    if father >= 0 && h.less(i, father) {
        h.swap(i, father)
        h.up(father)
    }
}
func (h Heap) down(i int) {
    smallest := i
    left := 2*i + 1
    right := 2*i + 2
    if left < len(h) && h.less(left, smallest) {
        smallest = left
    }
    if right < len(h) && h.less(right, smallest) {
        smallest = right
    }
    if smallest != i {
        h.swap(smallest, i)
        h.down(smallest)
    }
}
func (h *Heap) Push(v int) {
    *h = append(*h, v)
    h.up(len(*h) - 1)
}
func (h *Heap) Remove(i int) (int, bool) {
    if i < 0 || i >= len(*h) {
        return -1, false
    }
    x := (*h)[i]
    h.swap(i, len(*h)-1)
    *h = (*h)[:len(*h)-1]
    if i != len(*h) {
        h.down(i)
    }
    return x, true
}
func (h *Heap) Pop() int {
    x, _ := h.Remove(0)
    return x
}
// 写法二：优化
type SmallestInfiniteSet struct {
    heap Heap
    mp   map[int]bool
    idx  int
}

func Constructor() SmallestInfiniteSet {
    smallestInfiniteSet := SmallestInfiniteSet{}
    smallestInfiniteSet.mp = map[int]bool{}
    smallestInfiniteSet.idx = 1
    return smallestInfiniteSet
}

func (this *SmallestInfiniteSet) PopSmallest() int {
    res := -1
    if len(this.heap) != 0 {
        this.mp[this.heap[0]] = false
        res = this.heap.Pop()
    } else {
        res = this.idx
        this.idx++
    }
    return res
}

func (this *SmallestInfiniteSet) AddBack(num int) {
    if num >= this.idx || this.mp[num] {
        return
    }
    if num == this.idx-1 {
        this.idx--
    } else {
        this.heap.Push(num)
        this.mp[num] = true
    }
}
  • 时间复杂度：插入和取出的最坏复杂度为 O(logn)
  • 空间复杂度：O(n)

雇佣 K 位工人的总代价

2462. 雇佣 K 位工人的总代价 - 力扣（LeetCode）

给定一个数组表示雇佣各个工人的花费，给定整数k表示雇佣人数，给定整数candidates。选k轮，每轮选一个工人，从前candidates和后candidates人中选出花费最小的一个，若一样，选下标小的；若不足candidates人，则直接在剩余所有人里选一个花费最小的

思路：两个小顶堆，分别将前candidates和后candidates入两个堆，取出最小的，再入堆对应位置的一个，共取k次

注意：若工人数不足以选k轮，直接返回数组最小的k个元素即可，即len(costs) < candidates*2+k

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84

type Heap []int

func totalCost(costs []int, k int, candidates int) int64 {
    res := 0
    if len(costs) < candidates*2+k {
        sort.Slice(costs, func(i, j int) bool {
            return costs[i] < costs[j]
        })
        for i := 0; i < k; i++ {
            res += costs[i]
        }
    } else {
        heap1 := Heap(costs[:candidates])
        heap2 := Heap(costs[len(costs)-candidates:])
        heap1.Init()
        heap2.Init()
        left, right := candidates, len(costs)-candidates-1
        for i := 0; i < k; i++ {
            if heap1[0] <= heap2[0] {
                res += heap1.Pop()
                heap1.Push(costs[left])
                left++
            } else {
                res += heap2.Pop()
                heap2.Push(costs[right])
                right--
            }
        }
    }
    return int64(res)
}
func (h Heap) swap(i, j int) {
    h[i], h[j] = h[j], h[i]
}
func (h Heap) less(i, j int) bool {
    return h[i] < h[j]
}
func (h Heap) down(i int) {
    smallest := i
    left := 2*i + 1
    right := 2*i + 2
    if left < len(h) && h.less(left, smallest) {
        smallest = left
    }
    if right < len(h) && h.less(right, smallest) {
        smallest = right
    }
    if smallest != i {
        h.swap(i, smallest)
        h.down(smallest)
    }
}
func (h Heap) up(i int) {
    father := (i - 1) / 2
    if father >= 0 && h.less(i, father) {
        h.swap(father, i)
        h.up(father)
    }
}
func (h *Heap) Push(v int) {
    *h = append(*h, v)
    h.up(len(*h) - 1)
}
func (h *Heap) Remove(i int) (int, bool) {
    if i < 0 || i >= len(*h) {
        return -1, false
    }
    h.swap(i, len(*h)-1)
    x := (*h)[len(*h)-1]
    (*h) = (*h)[:len(*h)-1]
    if i != len(*h) {
        h.down(i)
    }
    return x, true
}
func (h *Heap) Pop() int {
    x, _ := h.Remove(0)
    return x
}
func (h Heap) Init() {
    for i := len(h)/2 - 1; i >= 0; i-- {
        h.down(i)
    }
}

最大子序列的分数

2542. 最大子序列的分数 - 力扣（LeetCode）

给定两个长度一样的数组，再给一个整数k，从第一个数组中选取长度为k的子序列，求出和，从第二个数组中选取子序列对应下标中的最小值；分数 = 和×最小值。返回最大分数

思路：贪心+小顶堆

降序重排nums2下标，枚举nums2[ids]最小，小顶堆求nums1前k大

  1. 对nums2的下标数组ids按元素值从大到小排序
  2. 将ids中前k个下标对应的nums1中元素值求和并入堆，求出一个分数
  3. 从第k+1个元素继续遍历下标数组ids，若nums1中该下标对应元素大于堆顶，则替换堆顶，求出分数与当前最大分数比较
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80

var heap []int

func maxScore(nums1 []int, nums2 []int, k int) int64 {
    // nums2下标降序重排
    ids := make([]int, len(nums2))
    for i := range ids {
        ids[i] = i
    }
    sort.Slice(ids, func(i, j int) bool {
        return nums2[ids[i]] > nums2[ids[j]]
    })
    // 枚举nums2[ids]最小 小顶堆求nums1前k大
    res := 0
    sum := 0
    heap = []int{}
    for i, v := range ids {
        if i < k {
            sum += nums1[v]
            Push(nums1[v])
            if i == k-1 {
                res = sum * nums2[v]
            }
        } else if nums1[v] > heap[0] {
            sum += nums1[v] - heap[0]
            Pop()
            Push(nums1[v])
            // 用新的sum 和 nums2[v]
            res = max(res, sum*nums2[v])
        }
    }
    return int64(res)
}
func swap(i, j int) {
    heap[i], heap[j] = heap[j], heap[i]
}
func less(i, j int) bool {
    return heap[i] < heap[j]
}
func up(i int) {
    father := (i - 1) / 2
    if father >= 0 && less(i, father) {
        swap(father, i)
        up(father)
    }
}
func down(i int) {
    smallest := i
    left := 2*i + 1
    right := 2*i + 2
    if left < len(heap) && less(left, smallest) {
        smallest = left
    }
    if right < len(heap) && less(right, smallest) {
        smallest = right
    }
    if smallest != i {
        swap(smallest, i)
        down(smallest)
    }
}
func Push(v int) {
    heap = append(heap, v)
    up(len(heap) - 1)
}
func remove(i int) (int, bool) {
    if i < 0 || i >= len(heap) {
        return -1, false
    }
    x := heap[i]
    swap(i, len(heap)-1)
    heap = heap[:len(heap)-1]
    if i != len(heap) {
        down(i)
    }
    return x, true
}
func Pop() int {
    x, _ := remove(0)
    return x
}

天际线问题

218. 天际线问题 - 力扣（LeetCode）

给一组三元组[lefti, righti, heighti]表示多个建筑物的位置和高度，返回由这些建筑物形成的天际线，关键点是水平线段的左端点

思路：由相邻两个横坐标以及最大高度，可以确定一个矩形

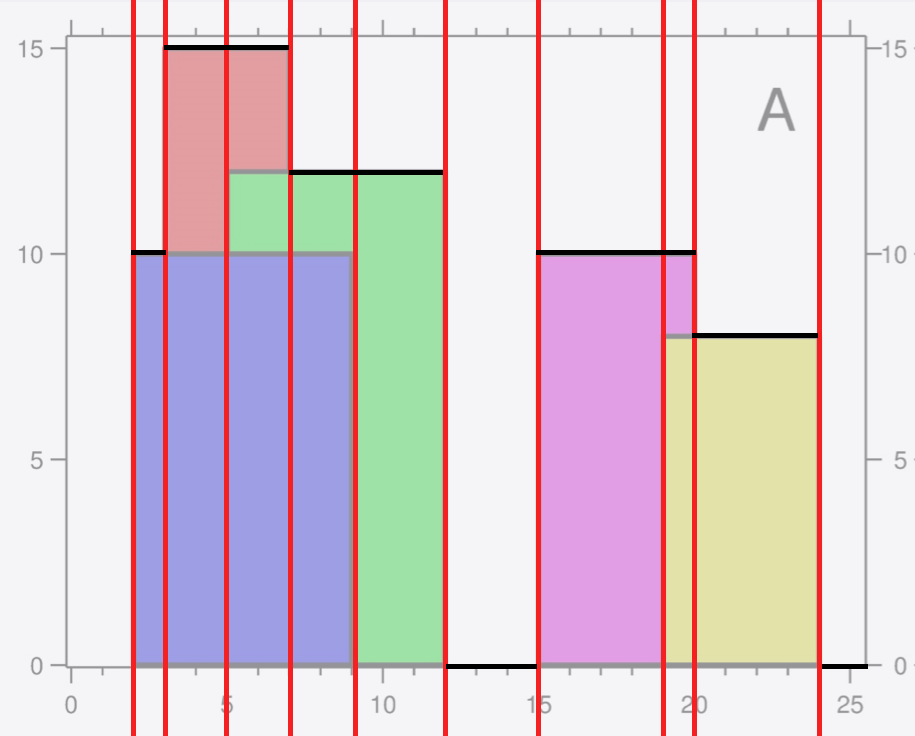
题目要求输出每个矩形的“最上边”的左端点，同时跳过可由前一矩形“上边”延展而来的那些边。因此需要维护一个最大高度，可以使用优先队列（堆）

实现时，先记录下 buildings 中所有的左右端点横坐标及高度，并根据端点横坐标从小到大排序

  1. 先严格按照横坐标进行「从小到大」排序

  2. 对于某个横坐标而言，可能会同时出现多个点，应当按照如下规则进行处理：

    • 优先处理左端点，再处理右端点
    • 如果同样都是左端点，则按照高度「从大到小」进行处理（将高度增加到优先队列中）
    • 如果同样都是右端点，则按照高度「从小到大」进行处理（将高度从优先队列中删掉）

在从前往后遍历处理时（遍历每个矩形），根据当前遍历到的点进行分情况讨论：

  • 左端点：因为是左端点，必然存在一条从右延展的边，但不一定是需要被记录的边，因为在同一矩形中，只需要记录最上边的边。这时候可以将高度进行入队

  • 右端点：此时意味着之前某一条往右延展的线结束了，这时候需要将高度出队（代表这条结束的线不再被考虑）

然后从优先队列中取出当前的最大高度，为了防止当前的线与前一矩形“最上边”延展而来的线重合，使用一个变量 prev 记录上一个记录的高度

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100

type Heap []int

func getSkyline(buildings [][]int) [][]int {
    res := [][]int{}

    // 预处理点:记录所有左右端点的横坐标及高度
    // 为了方便排序,对于左端点令高度为负,对于右端点令高度为正
    pos := [][]int{}
    for _, building := range buildings {
        pos = append(pos, []int{building[0], -building[2]})
        pos = append(pos, []int{building[1], building[2]})
    }
    // 先按照横坐标升序重排
    // 若横坐标相同,则左端点在前
    // 若同为左端点,则按原高度大的在前
    // 若同为右端点,则按原高度小的在前
    sort.Slice(pos, func(i, j int) bool {
        // 横坐标不同时升序重排
        if pos[i][0] != pos[j][0] {
            return pos[i][0] < pos[j][0]
        }
        // 横坐标相同时，左端点在前；同为左端点时高度大的在前；同为右端点时高度小的在前
        return pos[i][1] < pos[j][1]
    })

    // 大顶堆
    heap := Heap{}
    // 记录上一个记录的高度
    prev := 0
    heap.Push(prev)
    // 遍历所有预处理后的点
    for _, p := range pos {
        if p[1] < 0 {
            // 若为左端点,则高度入堆
            heap.Push(-p[1])
        } else {
            // 若为右端点,则高度出堆
            for i, v := range heap {
                if v == p[1] {
                    heap.Remove(i)
                    break
                }
            }
        }
        // 若当前最高高度不与前一矩形“最上边”延展而来的那些边重合,则记录
        if heap[0] != prev {
            res = append(res, []int{p[0], heap[0]})
            prev = heap[0]
        }
    }
    return res
}
func (h Heap) swap(i, j int) {
    h[i], h[j] = h[j], h[i]
}
func (h Heap) less(i, j int) bool {
    return h[i] > h[j]
}
func (h Heap) up(i int) {
    father := (i - 1) / 2
    if father >= 0 && h.less(i, father) {
        h.swap(i, father)
        h.up(father)
    }
}
func (h Heap) down(i int) {
    biggest := i
    left := i*2 + 1
    right := i*2 + 2
    if left < len(h) && h.less(left, biggest) {
        biggest = left
    }
    if right < len(h) && h.less(right, biggest) {
        biggest = right
    }
    if biggest != i {
        h.swap(i, biggest)
        h.down(biggest)
    }
}
func (h *Heap) Push(v int) {
    *h = append(*h, v)
    h.up(len(*h) - 1)
}
func (h *Heap) Remove(i int) (int, bool) {
    if i < 0 || i >= len(*h) {
        return -1, false
    }
    x := (*h)[i]
    h.swap(i, len(*h)-1)
    (*h) = (*h)[:len(*h)-1]
    if i != len(*h) {
        h.down(i)
    }
    return x, true
}
func (h *Heap) Pop() int {
    x, _ := h.Remove(0)
    return x
}

滑动窗口中位数

480. 滑动窗口中位数 - 力扣（LeetCode）

给一个数组 nums，有一个长度为 k 的窗口从最左端滑动到最右端。窗口中有 k 个数，每次窗口向右移动 1 位。找出每次窗口移动后得到的新窗口中元素的中位数，并输出由它们组成的数组。

思路：本题是「295. 数据流的中位数」的进阶版本

大顶堆保存前半部分，小顶堆保存后半部分 ，保持大顶堆元素个数比小顶堆元素个数不多于2个

由于堆不支持按值移除元素，所以可以使用「延迟删除」机制，用哈希表记录每个元素还需要被删除多少次，每次更新堆顶时判断是否需要被删除

由于删除元素改变了元素个数，所以也需要保持大顶堆元素个数比小顶堆元素个数不多于2个，小顶堆元素不多于大顶堆元素

可以编写一个「保持平衡」函数，维持大顶堆元素个数比小顶堆元素个数不多于2个，小顶堆元素不多于大顶堆元素

「清除无效堆顶」函数只需要在移除堆顶元素时，循环判新堆顶是否有效并清除，直到堆顶有效

自定义切片长度，记录切片逻辑长度（包括延迟删除），小于等于实际长度

注意：

  1. 由于是延迟删除，所以在标记删除元素时就要修改堆大小，避免影响「保持平衡」
  2. 在新入堆元素后，「保持平衡」中对移除堆顶元素的堆调用「清除无效堆顶」函数
  3. 由于堆中存在延迟删除元素，所以不能切片的长度属性判窗口内元素奇偶，可以直接用k；保持平衡函数中使用自定义切片长度
  4. 「清除无效堆顶」中循环终止条件是切片实际长度为0
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166

type Heap []int

var heap1 Heap
var heap2 Heap
var length1 int
var length2 int
var mp map[int]int
var winLength int

func medianSlidingWindow(nums []int, k int) []float64 {
    heap1, heap2 = Heap{}, Heap{}
    length1, length2 = 0, 0
    mp = map[int]int{}
    winLength = k
    // 初始化窗口
    for i := 0; i < k; i++ {
        // 元素入堆并保持平衡并保证堆顶有效
        insert(nums[i])
    }
    res := make([]float64, 1, len(nums)-k+1)
    res[0] = getMedian()
    // 移动窗口遍历nums
    for i := k; i < len(nums); i++ {
        insert(nums[i])
        // 标记删除元素
        erase(nums[i-k])
        // 得到当前窗口中位数
        res = append(res, getMedian())
    }
    return res
}

// 入堆并保持平衡
func insert(v int) {
    if len(heap1) == 0 || v <= heap1[0] {
        heap1.Push(v, true)
        length1++
    } else {
        heap2.Push(v, false)
        length2++
    }
    // 每添加一个元素都保持平衡
    makeBalance()
}

// 保持平衡并保证堆顶有效
func makeBalance() {
    if length1-length2 > 1 {
        heap2.Push(heap1.Pop(true), false)
        length1--
        length2++
        // 大顶堆堆顶元素被移除，需要判断新堆顶是否需要删除
        // 被大顶推移除的堆顶一定有效，所以不需要判小顶堆堆顶是否有效
        heap1.Prune(true)
    } else if length1 < length2 {
        heap1.Push(heap2.Pop(false), true)
        length2--
        length1++
        // 小顶堆堆顶元素被移除，需要判断新堆顶是否需要删除
        // 被小顶推移除的堆顶一定有效，所以不需要判大顶堆堆顶是否有效
        heap2.Prune(false)
    }
}

// 返回中位数
func getMedian() float64 {
    if winLength%2 == 1 {
        return float64(heap1[0])
    }
    return (float64(heap1[0]) + float64(heap2[0])) / 2.0
}

func erase(v int) {
    mp[v]++
    if v <= heap1[0] {
        // 更新逻辑长度
        length1--
        if v == heap1[0] {
            // 要延迟删除的元素就是堆顶元素,在Prune中更新哈希表后出堆
            heap1.Prune(true)
        }
    } else {
        length2--
        if v == heap2[0] {
            heap2.Prune(false)
        }
    }
    // 由于可能删除元素，所以需要保持平衡
    makeBalance()
}

func (h *Heap) Prune(sign bool) {
    for len(*h) > 0 {
        // 判堆顶是否无效
        if v, ok := mp[(*h)[0]]; ok {
            // 更新哈希表
            if v > 1 {
                mp[(*h)[0]]--
            } else {
                delete(mp, (*h)[0])
            }
            // 出堆
            h.Pop(sign)
        } else {
            break
        }
    }
}

func (h Heap) swap(i, j int) {
    h[i], h[j] = h[j], h[i]
}

func (h Heap) less(i, j int, sign bool) bool {
    if sign {
        return h[i] > h[j]
    }
    return h[i] < h[j]
}

func (h Heap) up(i int, sign bool) {
    father := (i - 1) / 2
    if father >= 0 && h.less(i, father, sign) {
        h.swap(i, father)
        h.up(father, sign)
    }
}

func (h Heap) down(i int, sign bool) {
    est := i
    left := i*2 + 1
    right := i*2 + 2
    if left < len(h) && h.less(left, est, sign) {
        est = left
    }
    if right < len(h) && h.less(right, est, sign) {
        est = right
    }
    if est != i {
        h.swap(est, i)
        h.down(est, sign)
    }
}

func (h *Heap) Push(v int, sign bool) {
    (*h) = append((*h), v)
    h.up(len(*h)-1, sign)
}

func (h *Heap) Remove(i int, sign bool) (int, bool) {
    if i < 0 || i >= len(*h) {
        return -1, false
    }
    x := (*h)[i]
    h.swap(i, len(*h)-1)
    (*h) = (*h)[:len(*h)-1]
    if i != len(*h) {
        h.down(i, sign)
    }
    return x, true
}

func (h *Heap) Pop(sign bool) int {
    x, _ := h.Remove(0, sign)
    return x
}
  • 时间复杂度：O(nlogn)。insert(num) 和 erase(num) 的单次时间复杂度为 O(logn)，getMedian() 的单次时间复杂度为 O(1)。因此总时间复杂度为 O(nlogn)
  • 空间复杂度：O(n)。即为 small，large 和 delayed 需要使用的空间

希尔排序

不建议多花时间了解

思想：插入排序的优化。在插入排序里，如果靠后的数字较小，它来到前面就得交换多次。「希尔排序」改进了这种做法。带间隔地使用插入排序，直到最后「间隔」为 1 的时候，就是标准的「插入排序」，此时数组里的元素已经「几乎有序」了；

希尔排序是一种基于插入排序的算法，但通过将待排序元素按照一定增量分组，使得不同组内的元素可以提前进行局部排序，从而提高了插入排序的效率。

希尔排序的「间隔序列」其实是一个超参数，这方面有一些研究成果，有兴趣的可以了解一下，如果是面向笔试面试，就不用了解了。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

func sortArray(nums []int) []int {
    // 初始增量h设为1
    h := 1

    // 使用 Knuth 增量序列
    // 找增量的最大值
    for 3*h+1 < len(nums) {
        h = 3*h + 1
    }

    for h >= 1 {
        // insertion sort 从索引h开始，直到数组末尾，对于每个索引i，执行insertionForDelta函数
        for i := h; i < len(nums); i++ {
            // 将nums[i]插入到间隔为gap的已排序序列中的正确位置，然后比较nums[j-gap]与temp，如果前一个大，则移动元素，否则停止并插入temp
            insertionForDelta(nums, h, i)
        }
        // 继续下一个较小的增量，直至h降至1以下
        h = h / 3
    }
    return nums
}

// 将 nums[i] 插入到对应分组的正确位置上，其实就是将原来 1 的部分改成 gap
func insertionForDelta(nums []int, gap int, i int) {
    // 将nums[i]暂存到temp
    temp := nums[i]
    j := i
    // 注意：这里 j >= gap 的原因(避免越界访问)
    for j >= gap && nums[j-gap] > temp {
        nums[j] = nums[j-gap]
        j -= gap
    }
    nums[j] = temp
}
  • Knuth增量序列：这是希尔排序的一个关键优化点，它选择增量序列的方式能够确保所有元素在最终排序完成前被充分地“打乱”，从而提高排序效率。
  • 插入排序变体：希尔排序可以看作是插入排序的一种变体，只是它在每次插入排序前先将数组分割成多个子序列，每个子序列通过较大的步长进行排序，这样可以减少数据的移动次数，从而提升效率。

希尔排序的时间复杂度依赖于增量序列的选择，最优情况下接近O(N3/2)O(N^{3/2})，最坏情况下可能是O(n2)O(n^2)，但通常比简单的插入排序快得多

冒泡排序

了解

  • 基本思想：外层循环每一次经过两两比较，把每一轮未排定部分最大的元素放到了数组的末尾

外层循环从末尾向前遍历，确定未排序部分结束位置；内层循环从首开始遍历未排序部分，若遇到当前元素大于下一元素，则交换，将大元素后置

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

func sortArray(nums []int) []int {
    for i := len(nums) - 1; i >= 0; i-- {
        for j := 0; j < i; j++ {
            if nums[j] > nums[j+1] {
                nums[j], nums[j+1] = nums[j+1], nums[j]
            }
        }
    }
    return nums
}
  • 时间复杂度：O(N2)O(N^2)，这里 NN 是数组的长度；
  • 空间复杂度：O(1)O(1)

下面是3种「非比较」的排序算法（了解，如果是面向笔试，不要花时间去研究），这部分算法不建议花太多去仔细研究它们的细节。如果是面向面试，了解思想即可，用到了再学

这三种排序的区别与上面的排序的特点是：一个数该放在哪里，是由这个数本身的大小决定的，它不需要经过比较。也可以认为是哈希的思想：由数值映射地址

因此这三种算法一定需要额外的空间才能完成排序任务，空间复杂度可以提升到 O(N)O(N)，但适用场景不多，主要是因为使用这三种排序一定要保证输入数组的每个元素都在一个合理的范围内

这三种算法还有一个特点是：都可以实现成稳定排序，无需稳定化

计数排序

了解

「计数排序」是这三种排序算法里最好理解的，从名字就可以看出。把每个出现的数值都做一个计数，然后根据计数从小到大输出得到有序数组。

这种做法丢失了稳定性，如果是本题这种基本数据类型的话没有关系。如果是对象类型，就不能这么做了。保持稳定性的做法是：先对计数数组做前缀和，在第 2 步往回赋值的时候，根据原始输入数组的数据从后向前赋值，前缀和数组保存了每个元素存放的下标信息

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

func sortArray(nums []int) []int {

    // 由于 -50000 <= A[i] <= 50000
    // 因此"桶" 的大小为 50000 - (-50000) = 100000
    // 并且设置偏移 OFFSET = 50000，目的是让每一个数都能够大于等于 0
    // 这样就可以作为 count 数组的下标，查询这个数的计数
    const OFFSET = 50000
    const size = 100002

    // 计数数组
    count := make([]int, size)

    // 计算计数数组
    for _, num := range nums {
        count[num+OFFSET]++
    }

    // 把 count 数组变成前缀和数组,每个元素变成比它小的所有元素的个数
    for i := 1; i < size; i++ {
        count[i] += count[i-1]
    }

    // 先把原始数组赋值到一个临时数组里，然后回写数据
    temp := make([]int, len(nums))
    copy(temp, nums)

    // 为了保证稳定性，从后向前赋值
    for i := len(nums) - 1; i >= 0; i-- {
        // index:小于或等于当前元素的元素数量
        index := count[temp[i]+OFFSET] - 1
        // 将当前元素 temp[i] 放置到已排序数组 nums 的正确位置上
        nums[index] = temp[i]
        // 将计数数组中当前元素的计数减1
        count[temp[i]+OFFSET]--
    }
    return nums
}
  • 时间复杂度： O(n+k)O(n + k)，n 是输入数组的长度，k 是输入数组中元素的范围，当 k 接近于 n 时，即输入数组中元素的范围很大时，计数排序的效率会降低。然而，在 k 远小于 n 的情况下，计数排序可以非常高效
  • 空间复杂度： O(n+k)O(n + k)，需要额外的计数数组和辅助数组

基数排序

了解

基本思路：也称为基于关键字的排序，例如针对数值排序，个位、十位、百位就是关键字。针对日期数据的排序：年、月、日、时、分、秒就是关键字。

「基数排序」用到了「计数排序」

整个过程涉及多轮的计数排序，每轮针对数字的一位进行排序。由于计数排序是稳定的，所以即使多次迭代，相同数字的相对顺序也不会改变，从而保证了基数排序的稳定性。最后，当所有位都被排序过后，再将结果中的每个数字减去OFFSET，还原原始值，得到最终的排序结果。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96

// 基数排序：低位优先
const OFFSET = 50000

func sortArray(nums []int) []int {
    length := len(nums)

    // 预处理，让所有的数都大于等于 0，这样才可以使用基数排序
    for i := range nums {
        nums[i] += OFFSET
    }

    // 第 1 步：找出最大的数字，用于后续计算最大位数
    max := nums[0]
    for _, num := range nums {
        if num > max {
            max = num
        }
    }

    // 第 2 步：计算出最大的数字有几位，这决定了排序的轮数
    maxLen := getMaxLen(max)

    // 计数排序需要使用的计数数组和临时数组
    // 统计0到9这十个数字的出现频率
    count := make([]int, 10)
    temp := make([]int, length)

    // 表征关键字的量：除数
    // 1 表示按照个位关键字排序
    // 10 表示按照十位关键字排序
    // 100 表示按照百位关键字排序
    // 1000 表示按照千位关键字排序
    divisor := 1
    // 有几位数，外层循环就得执行几次
    // 从最低位开始到最高位结束
    for i := 0; i < maxLen; i++ {

        // 每一步都使用计数排序，保证排序结果是稳定的
        // 这一步需要额外空间保存结果集，因此把结果保存在 temp 中
        // 对当前位上的数字进行计数排序
        countingSort(nums, temp, divisor, length, count)

        // 交换 nums 和 temp 的引用，下一轮还是按照 nums 做计数排序
        nums, temp = temp, nums

        // divisor 自增，表示采用低位优先的基数排序
        divisor *= 10
    }

    // 还原偏移量
    res := make([]int, length)
    for i := range nums {
        res[i] = nums[i] - OFFSET
    }
    return res
}

func countingSort(nums, res []int, divisor int, length int, count []int) {
    // 1、计算计数数组
    for i := 0; i < length; i++ {
        // 计算数位上的数是几，先取个位，再十位、百位
        remainder := (nums[i] / divisor) % 10
        // 根据当前位上的数字来更新计数数组
        count[remainder]++
    }

    // 2、变成前缀和数组
    for i := 1; i < 10; i++ {
        count[i] += count[i-1]
    }

    // 3、从后向前赋值
    for i := length - 1; i >= 0; i-- {
        remainder := (nums[i] / divisor) % 10
        index := count[remainder] - 1
        // 将数字放入正确的位置
        res[index] = nums[i]
        // 更新计数数组
        count[remainder]--
    }

    // 4、将计数数组重置为初始状态
    for i := range count {
        count[i] = 0
    }
}

// 获取一个整数的最大位数
func getMaxLen(num int) int {
    maxLen := 0
    for num > 0 {
        num /= 10
        maxLen++
    }
    return maxLen
}
  • 时间复杂度：O(d * (n + k))，n是数组的长度，d是最大的数的位数，但是，k通常是固定的（比如在十进制系统中k=10），所以时间复杂度可以简化为O(d * n)，d是最大数的位数，它通常与最大数的大小相关，但在很多情况下可以认为是常数，特别是当数字的范围是已知的并且不随问题规模变化时
  • 空间复杂度：O(n + k)，在每一次基数排序中，都需要一个长度为基数k的计数数组，空间复杂度为O(k)。对于十进制系统，k=10，所以这部分的空间复杂度是O(1)（在大多数情况下可以视为常数），简化后通常为O(n)

桶排序

了解

  • 基本思路：一个坑一个萝卜，也可以一个坑多个萝卜，对每个坑排序，再拿出来，整体就有序。

桶排序是一种分布式的排序算法，它将数组分到有限数量的“桶”中，每个桶再单独排序（通常使用其他排序算法，如插入排序）。然后，将桶中的元素有序地合并起来。这种方法特别适用于数据分布均匀的情况

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

const OFFSET = 50000

func sortArray(nums []int) []int {

    // 第 1 步：预处理
    // 将数据转换为 [0, 10_0000] 区间里的数，确保所有元素非负，便于后续操作
    for i := 0; i < len(nums); i++ {
        nums[i] += OFFSET
    }

    // 第 2 步：设置桶
    // 根据数据范围和内存限制，选择一个合适的步长，桶的个数由数据范围除以步长得到
    // 步长：步长如果设置成 10 会超出内存限制
    // 每个桶将存储步长范围内（例如，0-999，1000-1999等）的数字
    step := 1000
    // 桶的个数
    bucketLen := 10_0000 / step

    // 桶由二维数组temp表示，next数组记录每个桶中元素的数量
    temp := make([][]int, bucketLen+1)
    next := make([]int, bucketLen+1)

    // 第 3 步：分桶
    // 遍历数组，将每个元素放入相应的桶中
    for _, num := range nums {
        bucketIndex := num / step
        temp[bucketIndex] = append(temp[bucketIndex], num)
        next[bucketIndex]++
    }

    // 第 4 步：桶内排序
    // 对每个桶内的元素使用插入排序进行局部排序。这是因为桶内的元素已经大致归类，插入排序在这种情况下效率较高
    for i := 0; i < bucketLen+1; i++ {
        insertionSort(temp[i])
    }

    // 第 5 步：合并结果
    // 遍历所有桶，将桶中的元素按顺序取出，构成最终的排序结果
    res := make([]int, len(nums))
    index := 0
    for i := 0; i < bucketLen+1; i++ {
        curLen := next[i]
        for j := 0; j < curLen; j++ {
            // 在取出元素时，记得减去OFFSET，恢复原始值
            res[index] = temp[i][j] - OFFSET
            index++
        }
    }
    return res
}

func insertionSort(arr []int) {
    for i := 1; i < len(arr); i++ {
        temp := arr[i]
        j := i
        for j > 0 && arr[j-1] > temp {
            arr[j] = arr[j-1]
            j--
        }
        arr[j] = temp
    }
}
  • 时间复杂度：O(n)O(n)（最好情况：数据均匀分布在各个桶中，每个桶内的元素数量较少，桶内排序的时间复杂度可以视为接近常数）至O(n2)O(n^2)（最坏情况：数据分布不均，所有元素集中在少数几个桶中，或者一个桶内）
  • 空间复杂度：O(n+m)O(n+m)，m为桶的数量，在实践中，m通常远小于n，因此空间复杂度可以简化为O(n)O(n)

桶排序的时间和空间复杂度在很大程度上取决于数据的分布和桶的设置。在数据分布均匀且桶设置得当时，它可以提供非常好的性能。然而，当数据分布不均时，其性能可能会显著下降

相关题

前 K 个高频元素

347. 前 K 个高频元素 - 力扣（LeetCode）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

func topKFrequent(nums []int, k int) []int {
    mp := map[int]int{}
    for _, v := range nums {
        mp[v]++
    }
    // 相同频率的放同一个桶
    buckets := make([][]int, len(nums)+1)
    for k, v := range mp {
        if len(buckets[v]) == 0 {
            buckets[v] = make([]int, 0)
        }
        buckets[v] = append(buckets[v], k)
    }
    res := make([]int, 0, k)
    // 倒序遍历桶，取k个数
    for i := len(nums); i >= 1; i-- {
        if len(buckets[i]) != 0 {
            for j := 0; j < len(buckets[i]); j++ {
                res = append(res, buckets[i][j])
                if len(res) == k {
                    return res
                }
            }
        }
    }
    return res
}

  • 时间复杂度：O(n)，n 表示数组的长度。首先，遍历一遍数组统计元素的频率，这一系列操作的时间复杂度是 O(n)；桶的数量为 n+1，所以桶排序的时间复杂度为 O(n)；因此，总的时间复杂度是 O(n)。

  • 空间复杂度：很明显为 O(n)

0  字
评论
Powered by Waline v1.6.0
© 2021 - 2025 YI · 1348 Days
共叭叭了 2347124 字 · 182 篇文章

Built with Hugo
Theme Stack designed by Jimmy