哈希表

理论基础

哈希表（英文名字为Hash table，国内也有一些算法书籍翻译为散列表，这两个名称都是指hash table）

哈希表是根据关键码的值而直接进行访问的数据结构

官方的解释可能有点懵，其实直白来讲数组就是一张哈希表

哈希表中关键码就是数组的索引下标，然后通过下标直接访问数组中的元素，如下图所示：

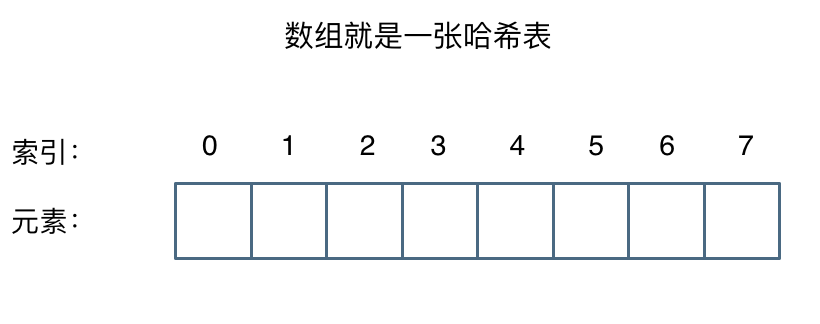
那么哈希表能解决什么问题呢，一般哈希表都是用来快速判断一个元素是否出现集合里

例如要查询一个名字是否在这所学校里，要枚举的话时间复杂度是O(n)，但如果使用哈希表的话，只需要O(1)就可以做到，只需要初始化把这所学校里学生的名字都存在哈希表里，在查询的时候通过索引直接就可以知道这位同学在不在这所学校里了

将学生姓名映射到哈希表上就涉及到了hash function ，也就是哈希函数

哈希函数

哈希函数如下图所示，通过hashCode把名字转化为数值，一般hashcode是通过特定编码方式，可以将其他数据格式转化为不同的数值，这样就把学生名字映射为哈希表上的索引数字了

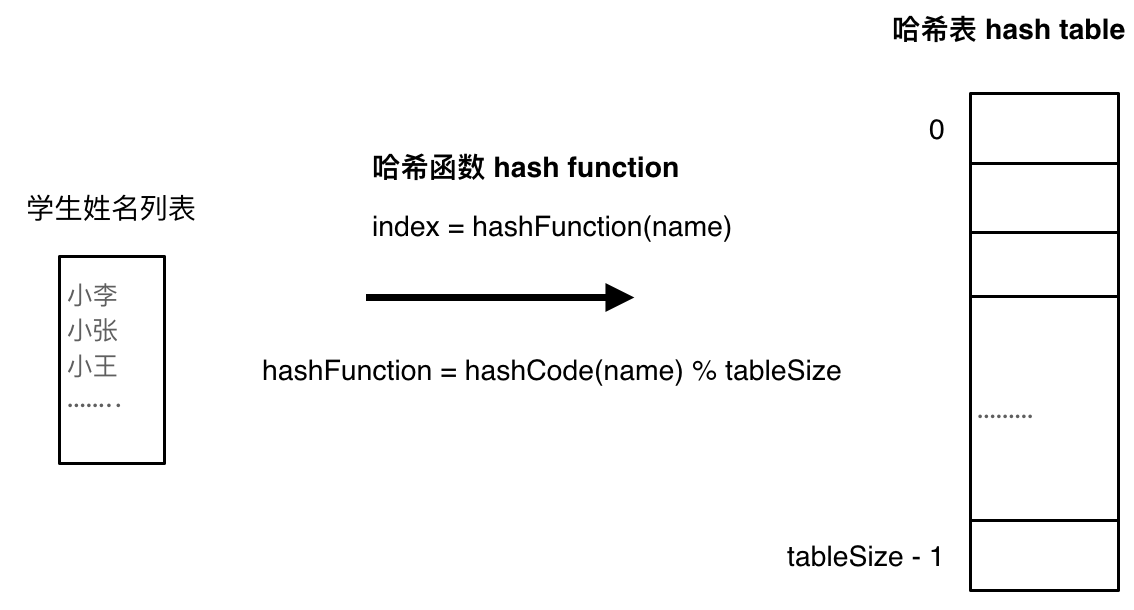
如果hashCode得到的数值大于哈希表的大小了，也就是大于tableSize了，怎么办呢

此时为了保证映射出来的索引数值都落在哈希表上，我们会在再次对数值做一个取模的操作，这样我们就保证了学生姓名一定可以映射到哈希表上了

此时问题又来了，哈希表我们刚刚说过，就是一个数组

如果学生的数量大于哈希表的大小怎么办，此时就算哈希函数计算的再均匀，也避免不了会有几位学生的名字同时映射到哈希表同一个索引下标的位置

接下来哈希碰撞登场

哈希碰撞

如图所示，小李和小王都映射到了索引下标 1 的位置，这一现象叫做哈希碰撞

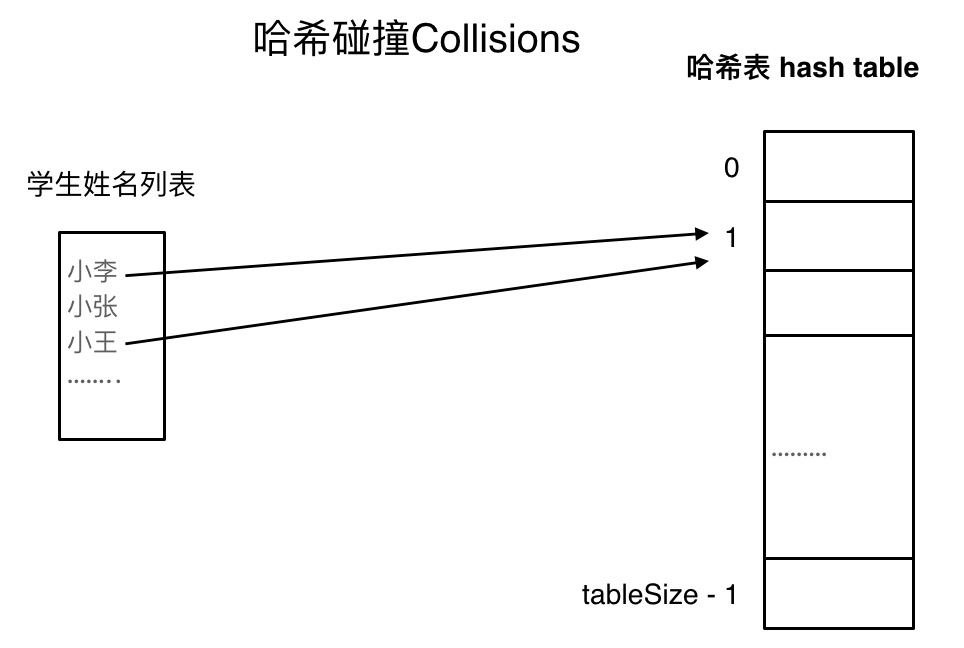
一般哈希碰撞有两种解决方法，拉链法和线性探测法

拉链法

刚刚小李和小王在索引1的位置发生了冲突，将发生冲突的元素都存储在链表中，这样我们就可以通过索引找到小李和小王了

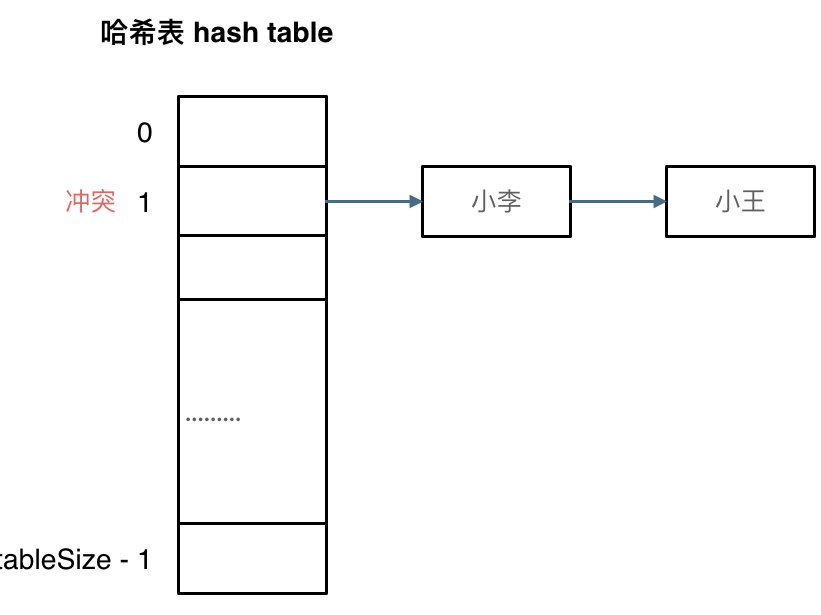
（数据规模是dataSize，哈希表的大小为tableSize）

其实拉链法就是要选择适当的哈希表的大小，这样既不会因为数组空值而浪费大量内存，也不会因为链表太长而在查找上浪费太多时间

线性探测法

使用线性探测法，一定要保证tableSize大于dataSize。我们需要依靠哈希表中的空位来解决碰撞问题

例如冲突的位置，放了小李，那么就向下找一个空位放置小王的信息。所以要求tableSize一定要大于dataSize ，要不然哈希表上就没有空置的位置来存放冲突的数据了。如图所示：

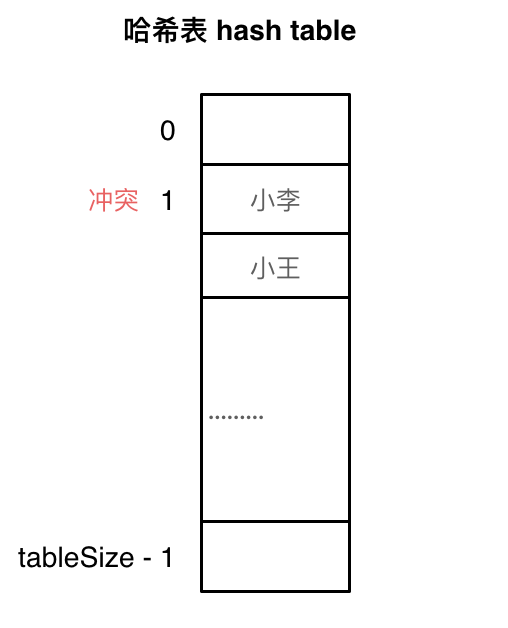
其实关于哈希碰撞还有非常多的细节，感兴趣的可以再好好研究一下，这里不再赘述

总结

总结一下，当我们遇到了要快速判断一个元素是否出现集合里的时候，就要考虑哈希法

但是哈希法也是牺牲了空间换取了时间，因为要使用额外的数组或map来存放数据，才能实现快速的查找

如果在做面试题目的时候遇到需要判断一个元素是否出现过的场景也应该第一时间想到哈希法

有效的字母异位词

242. 有效的字母异位词 - 力扣（LeetCode）

给定两个字符串 s 和 t ，编写一个函数来判断 s 和 t 是否互为字母异位词

注意：若 s 和 t 中每个字符出现的次数都相同，则称 s 和 t 互为字母异位词

map

先分别遍历两个字符串并存入同一map，s 负责在对应位置增加，t 负责在对应位置减少，最后遍历map若有值不为 0，则不是字母异位词，否则是字母异位词

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


func isAnagram(s string, t string) bool {
    charMap := make(map[rune]int)
    for _, sRune := range s { // 遍历字符串s
        charMap[sRune]++ // 对应字符加一
    }
    for _, tRune := range t { // 遍历字符串t
        charMap[tRune]-- // 对应字符减一
    }
    for _, v := range charMap { // 遍历字典
        if v != 0 { // 有字符数量不等
            return false
        }
    }
    return true
} 

时间复杂度：O(n)
空间复杂度：O(1)

数组

定义一个长度为26的数组，分别遍历两个字符串，将字符减去字符a（ASCII）得到字符在数组中的索引，s 负责在对应位置增加，t 负责在对应位置减少，最后遍历数组若有值不为 0，则不是字母异位词，否则是字母异位词

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


func isAnagram(s string, t string) bool {
    array := [26]int{}
    for i := 0; i < len(s); i++ { // 遍历字符串s
        array[s[i]-'a']++ // 对应字符数加一
    }
    for i := 0; i < len(t); i++ { // 遍历字符串t
        array[t[i]-'a']-- // 对应字符数减一
    }
    for _, v := range array { // 遍历数组
        if v != 0 { // 遇到有字符不等
            return false
        }
    }
    return true
}

时间复杂度：O(n)
空间复杂度：O(1)

赎金信

383. 赎金信 - 力扣（LeetCode）

给定两个字符串：ransomNote 和 magazine ，判断 ransomNote 能不能由 magazine 里面的字符构成，如果可以，返回 true ；否则返回 false ，magazine 中的每个字符只能在 ransomNote 中使用一次

数组：遍历magazine，对应字符减去a映射到数组索引，每有一个该字符，对应数组值加一；遍历ransonNote，每个字符映射到数组索引，若该字符数组值为0，返回false，否则每用一个字符，字符减一，若能遍历结束，则返回true

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


func canConstruct(ransomNote string, magazine string) bool {
    alpha := [26]int{}
    for i := 0; i < len(magazine); i++ { // 遍历magazine
        alpha[magazine[i]-'a']++ // 对应字符数组值加一
    }
    for i := 0; i < len(ransomNote); i++ { // 遍历ransomNote
        if alpha[ransomNote[i]-'a'] == 0 { // 没有该字符的储备
            return false
        }
        alpha[ransomNote[i]-'a']-- // 对应字符储备减一
    }
    return true
}

时间复杂度：O(n+m)
空间复杂度：O(1)

字母异位词分组

49. 字母异位词分组 - 力扣（LeetCode）

给定一个字符串数组，返回一个二维数组，一维数组中的每个元素互为字母异位词，可以按任意顺序返回结果集，字母异位词是由重新排列源单词的所有字母得到的一个新单词

数组

数组：两层for循环，外层循环逐个遍历给定字符串数组，遇到没加入过结果集的，将字符串的每个字符映射到数组索引，个数存入数组值；内层循环从外层循环的下一个元素开始逐个遍历给定字符串数组，若该字符串与外层字符串互为字母异位词，则存入结果集，然后将内层该字符串元素标记为加入过结果集，内层继续遍历，寻找下一字母异位词

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43


func groupAnagrams(strs []string) [][]string {
    res := make([][]string, 0)
    for i := 0; i < len(strs); i++ { // 遍历字符串数组
        if strs[i] == "added" {
            continue // 遇到加入过的数组跳过
        }
        alpha := [26]int{}
        for _, char := range strs[i] { // 遍历字符串
            alpha[char-'a']++ // 对应字符数组值加一
        }
        tempRes := make([]string, 0)
        tempRes = append(tempRes, strs[i])
        for j := i + 1; j < len(strs); j++ { // 遍历字符串数组
            if strs[i] == "added" {
                continue // 遇到加入过的数组跳过
            }
            tempAlpha := alpha
            isCanJ := true                 // 默认该字符串能被外层字符串构成
            for _, char := range strs[j] { // 遍历字符串
                if tempAlpha[char-'a'] == 0 { // 没有该字符储备
                    isCanJ = false // 该字符串不能被外层字符串构成
                    break          // 遍历下一字符串
                }
                tempAlpha[char-'a']-- // 对应字符数组值加一
            }
            if isCanJ { // 该字符串能被外层字符串构成
                isGroup := true               // 默认内外层字符串互为字母异位词
                for _, v := range tempAlpha { // 遍历临时字典
                    if v != 0 { // 外层字符串不能由内层字符串构成
                        isGroup = false
                        break
                    }
                }
                if isGroup { // 内外层字符串互为字母异位词
                    tempRes = append(tempRes, strs[j]) // 将该字符串加入临时结果集
                    strs[j] = "added"                  // 在字符串数组中将该字符串标记
                }
            }
        }
        res = append(res, tempRes) // 将字母异位词加入结果集
    }
    return res
}

时间复杂度：O(n²)
空间复杂度：O(n)

map：key是字母表，value是字符串数组

遍历字符串数组，用数组记录每个字符的个数，用该数组作为字典的key，对应字符串作为字典的value，最后遍历map，将value存入结果集返回

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


func groupAnagrams(strs []string) [][]string {
	mp := make(map[[26]int][]string)
	for _, str := range strs { // 遍历字符串数组
		alpha := [26]int{}
		for _, char := range str { // 统计该字符串中各字符数
			alpha[char-'a']++ // 对应字符数值加一
		}
		mp[alpha] = append(mp[alpha], str) // 将具有相同字符数的字符串加入字典值
	}
	res := make([][]string, 0)
	for _, v := range mp { // 遍历字典值
		res = append(res, v)
	}
	return res
}

时间复杂度：O(n)
空间复杂度：O(n)

找到字符串中所有字母异位词

438. 找到字符串中所有字母异位词 - 力扣（LeetCode）

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。

数组

遍历p统计字符个数；逐个遍历s，每次取p中字符个数，判断是否能用完数组中保存的值，若可以，则存入结果集

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


func findAnagrams(s string, p string) []int {
    alpha := [26]int{}
    res := make([]int, 0)
    for _, ch := range p { // 遍历字符串p
        alpha[ch-'a']++ // 对应字符数组值加一
    }
    for i := 0; i < len(s)-len(p)+1; i++ { // 遍历字符串s
        tempAlpha := alpha
        j := i             // 标记子串起始位置
        for range len(p) { // 取p中字符个数
            tempAlpha[s[j]-'a']-- // 对应字符数组值减一
            j++                   // 取子串中下个字符
        }
        isGroup := true               // 默认子串与p互为字母异位词
        for _, v := range tempAlpha { // 遍历数组
            if v != 0 { // 有数组值不为0
                isGroup = false //子串与p不互为字母异位词
                break
            }
        }
        if isGroup {
            res = append(res, i) // 子串起始索引追加到结果集
        }
    }
    return res
}

时间复杂度：O(n)
空间复杂度：O(1)

滑动窗口+数组

在s上维持一个窗口大小为26的滑动窗口，每次滑动删除一个旧字符，添加一个新字符，比较窗口数组与统计的p字符数的数组是否相等，若相等则互为字母异位词

滑动窗口两种形式：

窗口大小未定：需要声明双指针指向左右边界，根据条件移动左右边界
窗口大小已定：只需要声明窗口，滑动时根据窗口大小更新边界元素进出

注意

在统计p中字符数时同时在s上初始化窗口
为了保持进出窗口操作的一致性，初始化完窗口需要先比较一次
循环变量i是窗口的右边界，左边界是i-len(p)+1，也就是子串开始索引
若len(s)<len(p)直接返回空

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


func findAnagrams(s string, p string) []int {
    if len(s) < len(p) {
        return []int{}
    }
    alpha, window := [26]int{}, [26]int{}
    res := make([]int, 0)
    for i := 0; i < len(p); i++ {
        alpha[p[i]-'a']++  // 统计p中字符数
        window[s[i]-'a']++ // 初始化s上窗口
    }
    if alpha == window {
        res = append(res, 0) // 记录第一个异位词索引0
    }
    for i := len(p); i < len(s); i++ { // 遍历s
        window[s[i-len(p)]-'a']-- // 删除窗口中旧元素
        window[s[i]-'a']++        // 向窗口中添加新元素
        if alpha == window {
            res = append(res, i-len(p)+1) // 记录新增异位词索引
        }
    }
    return res
}

时间复杂度：O(n)
空间复杂度：O(1)

两个数组的交集

349. 两个数组的交集 - 力扣（LeetCode）

给定两个数组 nums1 和 nums2 ，返回 它们的交集，交集中的每个元素要是唯一的，不考虑输出结果的顺序

map：遍历nums1，数字作为key，对应值为true；遍历nums2，若能找到对应数字且为true，则存入结果集，然后将其置为false

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


func intersection(nums1 []int, nums2 []int) []int {
    mapping := make(map[int]bool)
    res := make([]int, 0)
    for _, v := range nums1 { // 遍历nums1
        mapping[v] = true // 对应数字置为true
    }
    for _, v := range nums2 { // 遍历nums2
        if val, ok := mapping[v]; ok { // 在字典中
            if val == true { // 字典值为true
                res = append(res, v) // 存入结果集
                mapping[v] = false   // 更新字典
            }
        }
    }
    return res
}

时间复杂度：O(n+m)
空间复杂度：O(n)

优化空间：用struct{}定义了一个空结构体类型，该类型不包含任何字段，用struct{}{}则表示创建了一个空的结构体实例，不占用任何内存空间，被用作占位符或者标记，表示只关心键的存在与否而不需要实际存储值

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


func intersection(nums1 []int, nums2 []int) []int {
    mapping := make(map[int]struct{})
    res := make([]int, 0)
    for _, v := range nums1 { // 遍历nums1
        if _, ok := mapping[v]; !ok { // 字典中不存在
            mapping[v] = struct{}{}
        }
    }
    for _, v := range nums2 { // 遍历nums2
        if _, ok := mapping[v]; ok { // 在字典中
            res = append(res, v) // 存入结果集
            delete(mapping, v)   // 更新字典
        }
    }
    return res
}

时间复杂度：O(n+m)
空间复杂度：O(n)

两个数组的交集 II

350. 两个数组的交集 II - 力扣（LeetCode）

给定两个数组 nums1 和 nums2 ，返回 它们的交集，交集中的每个元素取两个数组中出现次数较小值，不考虑输出结果的顺序

map：遍历nums1，数字作为key，出现次数作为value，遍历nums2，若字典中有该数字且value大于0，则将数字存入结果集，然后字典中该数字的value减一

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


func intersect(nums1 []int, nums2 []int) []int {
    mp := make(map[int]int)
    res := make([]int, 0)
    for _, v := range nums1 { // 遍历nums1
        mp[v]++ // 对应数字个数加一
    }
    for _, v := range nums2 { // 遍历nums2
        if val, ok := mp[v]; ok && val > 0 { // 字典中有该数字且次数大于0
            res = append(res, v) // 存入结果集
            mp[v]--              // 对应数字个数减一
        }
    }
    return res
}

时间复杂度：O(n+m)
空间复杂度：O(n)

快乐数

202. 快乐数 - 力扣（LeetCode）

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1，那么这个数就是快乐数。

如果 n 是 快乐数 就返回 true ；不是，则返回 false

思路一：哈希表

map：记录每个平方和，若求出的平方和之前出现过，则是无限循环，返回false

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


func isHappy(n int) bool {
    mp := make(map[int]struct{})
    sum := 0
    for sum != 1 {
        sum = 0      // 清空平方和
        for n != 0 { // 求平方和
            digit := n % 10      // 取一位
            sum += digit * digit // 记录平方值
            n = n / 10           // 更新n
        }
        if _, ok := mp[sum]; ok { // 出现过该平方和
            return false
        }
        mp[sum] = struct{}{} // 记录该平方和
        n = sum              // 更新n
    }
    return true
}

时间复杂度：O(logn)
空间复杂度：O(logn)

思路二：快慢指针

通过反复调用 getNext(n) 得到的链是一个隐式的链表。隐式意味着没有实际的链表节点和指针，但数据仍然形成链表结构。起始数字是链表的头 “节点”，链中的所有其他数字都是节点。next 指针是通过调用 getNext(n) 函数获得。这个问题就可以转换为检测一个链表是否有环。

如果 n 是一个快乐数，即没有循环，那么快跑者最终会比慢跑者先到达数字 1
如果 n 不是一个快乐的数字，那么最终快跑者和慢跑者将在同一个数字上相遇

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


func isHappy(n int) bool {
    // 获取n的各位平方和
    getNext := func(n int) int {
        sum := 0
        for n != 0 {
            sum += (n % 10) * (n % 10)
            n /= 10
        }
        return sum
    }
    // 初始化快慢指针指向n和n的各位平方和
    slow, fast := n, getNext(n)
    // 当快慢指针未相遇或快指针未到1时不断循环
    for slow != fast && fast != 1 {
        // 每次慢指针前进一步快指针前进两步
        slow = getNext(slow)
        fast = getNext(getNext(fast))
    }
    // 判是有环还是快指针指向1
    return fast == 1
}

时间复杂度：O(logn)
空间复杂度：O(1)

两数之和

1. 两数之和 - 力扣（LeetCode）

给定一个整数数组 nums 和一个整数目标值 target，在该数组中找出和为目标值 target 的那两个整数，并返回它们的数组下标

map：遍历数组，每遍历到一个元素val，就target-val作为key在map中查找是否存在，若存在，说明找到两个目标整数，返回它们的下标，若不存在，将当前遍历整数作为key，下标作为value存入map

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


func twoSum(nums []int, target int) []int {
    mp := make(map[int]int)
    for i, v := range nums {
        if val, ok := mp[target-v]; ok { // 字典中找到另一个数
            return []int{val, i}
        } else {
            mp[v] = i // 将当前元素加入字典
        }
    }
    return []int{}
}

时间复杂度：O(n)
空间复杂度：O(n)

四数相加 II

454. 四数相加 II - 力扣（LeetCode）

给定四个数组，每个数组中取一个元素使其加和等于零，返回所有可能的组数

map：a+b作为key，出现次数作为value；遍历前两个数组，记录所有可能的两数和及其出现次数，再遍历后两个数组，若遇到0-(c+d)在字典中出现，则统计其出现次数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


func fourSumCount(nums1 []int, nums2 []int, nums3 []int, nums4 []int) int {
    mp := make(map[int]int)
    res := 0
    for _, a := range nums1 {
        for _, b := range nums2 {
            mp[a+b]++ // 统计a+b的出现次数
        }
    }
    for _, c := range nums3 {
        for _, d := range nums4 {
            res += mp[-c-d] // 记录结果
        }
    }
    return res
}

时间复杂度：O(n²)
空间复杂度：O(n²)，最坏情况a+b值各不相同，相加产生的数字个数为n²

三数之和

15. 三数之和 - 力扣（LeetCode）

给定一个数组，从数组中取三个元素组成一个长度为3的组合，要求和为0，返回所有可能的组合，注意组合不能重复

哈希：两层for循环确定a和b的数值，可以使用哈希法来确定 0-(a+b) 是否在数组里出现过，但去重的过程不好处理，有很多小细节，如果在面试中很难想到位

双指针（三指针）：先对数组排序，方便去重；用循环变量i遍历数组，左指针left指向i的下一个元素，右指针指向数组末尾；先检查i是否大于0，由于数组已排序，i指向元素一定是最小的，所以后面不会找到另两个元素组成组合和等于0，直接跳出循环；再检查i指向的元素是否与前面的元素重复，若重复说明组合会重复，直接跳过本次i；若左指针小于右指针，判断三个指针指向元素和是否为0，若等于，将三个元素加入结果集，然后判断左指针元素是否和其后面元素相等，若相等，为了避免重复集合，左指针进入内部循环后移（直至最后一个同值元素），再判断右指针元素是否和其前面元素相等，若相等，为了避免重复集合，右指针进入内部循环前移（直至第一个同值元素），随后左指针后移，右指针前移；若三个指针指向元素小于0，左指针后移；若三个指针指向元素大于0，右指针前移

注意：去重逻辑应该放在找到一个三元组之后，如果放在前面，可能直接导致 right<=left 了，从而漏掉了 0,0,0 这种三元组

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46


func threeSum(nums []int) [][]int {
    res := make([][]int, 0)
    // 升序重排
    sort.Ints(nums)
    // 三指针
    for idx1 := 0; idx1 < len(nums)-2; idx1++ {
        // 判断组中最小值是否大于0
        if nums[idx1] > 0 {
            // 结束遍历
            break
        }
        // idx1去重(第一次出现时使用,若后续有重复可以让left,right都用到一次)
        if idx1 != 0 && nums[idx1] == nums[idx1-1] {
            // 跳过该元素
            continue
        }
        // 初始化左右指针指向idx1+1和尾,按条件移动,直到相遇
        for left, right := idx1+1, len(nums)-1; left < right; {
            // 判断是否找到目标三元组
            if nums[idx1]+nums[left]+nums[right] == 0 {
                // 加入结果集
                res = append(res, []int{nums[idx1], nums[left], nums[right]})
                // left去重
                for left < right && nums[left] == nums[left+1] {
                    // left后移寻找最后一个left值
                    left++
                }
                // right去重
                for left < right && nums[right] == nums[right-1] {
                    // right前移寻找第一个right值
                    right--
                }
                // 移动left right指向新值
                left++
                right--
            } else if nums[idx1]+nums[left]+nums[right] < 0 {
                // 左指针后移,增大值
                left++
            } else {
                // 右指针前移,缩小值
                right--
            }
        }
    }
    return res
}

时间复杂度：O(n²)
空间复杂度：O(1)

四数之和

18. 四数之和 - 力扣（LeetCode）

给定一个数组和目标值，从数组中取四个元素组成一个长度为4的组合，要求和为目标值，返回所有可能的组合，注意组合不能重复

双指针（四指针）：两层for循环nums[k] + nums[i]为确定值，循环内有left和right下标作为双指针，找出四个值和等于目标值的情况

注意：

不要判断nums[k] > target 就返回了，三数之和可以通过 nums[i] > 0 就返回了，因为 0 已经是确定的数了，四数之和这道题目 target是任意值。比如：数组是[-4, -3, -2, -1]，target是-10，不能因为-4 > -10而跳过。但是依旧可以去做剪枝，逻辑变成nums[i] > target && (nums[i] >=0 || target >= 0)就可以了

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40


func fourSum(nums []int, target int) [][]int {
    sort.Ints(nums)
    res := make([][]int, 0)
    for i := 0; i < len(nums)-3; i++ { // i遍历到倒数第四个
        if nums[i] > target && nums[i] >= 0 { // 组合中最小值都大于目标值且组合中最小值为正数
            break // 跳出循环
        }
        if i > 0 && nums[i] == nums[i-1] { // i指向元素不是第一个元素且与其前一个元素相等
            continue // 跳过本次循环,向后寻找新元素(对i去重)
        }
        for k := i + 1; k < len(nums)-2; k++ { // k遍历到倒数第三个
            if nums[i]+nums[k] > target && (nums[i]+nums[k] >= 0){// 组合中俩最小值都大于目标值且组合中俩最小值为正数
                break // 跳出循环
            }
            if k > i+1 && nums[k] == nums[k-1] { // k指向元素不是第一个元素且与其前一个元素相等
                continue // 跳过本次循环,向后寻找新元素(对k去重)
            }
            left := k + 1          // 左指针初始指向k下一个
            right := len(nums) - 1 // 右指针初始指向数组末尾
            for left < right {     // 左右指针不断移动
                if nums[i]+nums[k]+nums[left]+nums[right] == target { // 和为target
                    res = append(res, []int{nums[i], nums[k], nums[left], nums[right]}) // 记录结果
                    for left < right && nums[left] == nums[left+1] {  // 左指针指向元素与其后一个元素相等
                        left++ // 左指针后移,向后寻找最后一个left值(对left去重)
                    }
                    for left < right && nums[right] == nums[right-1] { // 右指针指向元素与其前一个元素相等
                        right-- // 右指针前移,向前寻找第一个right值(对right去重)
                    }
                    left++  // 左指针后移
                    right-- // 右指针前移
                } else if nums[i]+nums[k]+nums[left]+nums[right] > target { // 和大于target
                    right-- // 右指针前移,缩小值
                } else { // 和小于target
                    left++ // 左指针后移,增大值
                }
            }
        }
    }
    return res
}

时间复杂度：O(n²)
空间复杂度：O(1)

最长连续序列

128. 最长连续序列 - 力扣（LeetCode）

给定一个未排序的整数数组，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度，设计并实现时间复杂度为 O(n) 的算法解决此问题

思路：先遍历数组，将所有元素作为key存入字典，字典值为bool型；再遍历字典key，判断当前元素是否为一个连续序列开头，若其前一个数字在字典中不存在，则说明当前元素是一个连续序列的开头，不断在字典中查找该连续序列的下一个元素并记录序列长度

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


func longestConsecutive(nums []int) int {
    res := 0
    mp := make(map[int]bool)
    // 遍历数组存入字典
    for _, v := range nums {
        mp[v] = true
    }
    // 遍历字典
    for k := range mp {
        // 判断当前元素是否为一个连续序列开头
        if !mp[k-1] {
            // 从当前元素开始找连续序列
            cur := k
            length := 1
            // 循环找下一元素
            for mp[cur+1] {
                // 更新当前元素和序列长度
                cur++
                length++
            }
            // 判断当前连续序列长度是否大于结果
            if length > res {
                // 更新结果
                res = length
            }
        }
    }
    return res
}

时间复杂度：$O(n)$
空间复杂度：$O(n)$

思路二：贪心

思路：升序重排数组，不断统计当前连续序列长度，每统计结束一个连续序列就同时更新目前最长连续序列长度

注意：遇到当前元素与前一元素相同直接跳过

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


func longestConsecutive(nums []int) int {
    if len(nums) == 0 {
        return 0
    }
    // 升序重排
    sort.Ints(nums)
    // 记录目前最长连续序列长度
    res := 0
    // 记录目前连续序列长度
    curLength := 1
    // 遍历数组
    for i := 1; i < len(nums); i++ {
        // 判断是否连续
        if nums[i] == nums[i-1]+1 {
            // 目前连续序列长度加一
            curLength++
        } else if nums[i] == nums[i-1] {
            // 与前一元素相同直接跳过
            continue
        } else {
            // 统计目前最长连续序列长度
            res = max(res, curLength)
            // 重置目前连续序列长度
            curLength = 1
        }
    }
    // 统计目前最长连续序列长度
    res = max(res, curLength)
    return res
}

时间复杂度：$O(nlog⁡n)$，主要为快排时间复杂度
空间复杂度：$O(log⁡n)$，主要为快排栈空间

同构字符串

205. 同构字符串 - 力扣（LeetCode）

给定两个字符串 s 和 t ，判断它们是否是同构的。如果 s 中的字符可以按某种映射关系替换得到 t ，那么这两个字符串是同构的。每个出现的字符都应当映射到另一个字符，同时不改变字符的顺序。不同字符不能映射到同一个字符上，相同字符只能映射到同一个字符上，字符可以映射到自己本身。

思路一：使用两个map保存 s[i] 到 t[i] 和 t[i] 到 s[i] 的映射关系，如果发现对应不上，立刻返回 false

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44


// 写法一
func isIsomorphic(s string, t string) bool {
    mp1, mp2 := make(map[byte]byte), make(map[byte]byte)
    for i := range s {
        // 判断s[i]是否没有到t[i]的映射
        if _, ok := mp1[s[i]]; !ok {
            // 设置s[i]映射到t[i]
            mp1[s[i]] = t[i]
        }
        // 判断t[i]是否没有到s[i]的映射
        if _, ok := mp2[t[i]]; !ok {
            // 设置t[i]映射到s[i]
            mp2[t[i]] = s[i]
        }
        // 判断是否映射不对应
        if mp1[s[i]] != t[i] || mp2[t[i]] != s[i] {
            return false
        }
    }
    return true
}
// 写法二
func isIsomorphic(s string, t string) bool {
    // 遍历串s和t 构建一一映射关系 判断关系是否唯一
    mp1 := map[byte]byte{}
    mp2 := map[byte]bool{}
    for i := 0; i < len(s); i++ {
        // 判s当前字符是否已存在映射
        if v, ok := mp1[s[i]]; ok {
            // 判已有映射与当前t字符是否一致
            if v != t[i] {
                return false
            }
        } else {
            // 判t当前字符是否已被映射
            if mp2[t[i]] {
                return false
            }
            mp1[s[i]] = t[i]
            mp2[t[i]] = true
        }
    }
    return true
}

时间复杂度：$O(n)$
空间复杂度：$O(n)$

查找共用字符

1002. 查找共用字符 - 力扣（LeetCode）

给定一个字符串数组 words ，找出所有在 words 的每个字符串中都出现的共用字符（包括重复字符），并以数组形式返回。可以按 任意顺序 返回答案。

思路：统计出每个元素里26个字符的出现频率，然后取频率的最小值，最后转成输出格式

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


func commonChars(words []string) []string {
    // 保存各个字符在所有元素中的最少出现次数
    count := [26]int{}
    // 统计第一个元素中各字符出现次数
    for _, ch := range words[0] {
        count[ch-'a']++
    }
    // 遍历数组(从第二个元素开始)
    for i := 1; i < len(words); i++ {
        temp := [26]int{}
        // 遍历该元素中所有字符
        for _, ch := range words[i] {
            temp[ch-'a']++
        }
        // 更新count
        for j := 0; j < 26; j++ {
            count[j] = min(count[j], temp[j])
        }
    }
    res := make([]string, 0)
    // 遍历统计结果
    for i, v := range count {
        // 循环重复次数
        for j := 0; j < v; j++ {
            // 计入结果集
            res = append(res, string(i+'a'))
        }
    }
    return res
}

时间复杂度：$O(n*m)$
空间复杂度：$O(1)$

长按键入

925. 长按键入 - 力扣（LeetCode）

朋友正在使用键盘输入他的名字。偶尔在键入字符时，按键可能会被长按，字符可能被输入 1 次或多次，现需要检查键盘输入的字符 typed，如果它对应的可能是朋友的名字（其中一些字符可能被长按），那么就返回 True，否则返回False

思路：模拟同时遍历两个数组，进行对比就可以了

name[i]和typed[j]相同，则i++，j++ （继续向后对比）
name[i]和typed[j]不相同
- 看是不是第一位就不相同了，也就是i如果等于0，那么直接返回false
- 不是第一位不相同，就让typed[j]和name[i-1]比较
  - 若相同，说明是重复字符，则只让j++ （去重），i不动
  - 若不相同，说明不是重复字符，是错误输入，则直接返回false
对比完之后有两种情况
- name没有匹配完，说明输入一定错误，因为输入字符的长度都不够
- type没有匹配完，则让type后续字符和name最后一个字符继续比较，一旦有不同，则返回false

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


func isLongPressedName(name string, typed string) bool {
    idx1, idx2 := 0, 0
    for idx1 != len(name) && idx2 != len(typed) {
        // 判断字符是否不相等
        if name[idx1] != typed[idx2] {
            // 判断是否第一个就不同或键入非重复性错误字符
            if idx1 == 0 || typed[idx2] != name[idx1-1] {
                return false
            } else {
                // 键入重复字符,去重
                idx2++
                continue
            }
        }
        // 同时后移,比较下一字符
        idx1++
        idx2++
    }
    // name没有匹配完
    if idx1 != len(name) && idx2 ==len(typed) {
        return false
    }
    // type没有匹配完
    for idx2 != len(typed) {
        // 判断键入字符是否和name最后一个字符不同
        if typed[idx2] != name[idx1-1] {
            return false
        } else {
            idx2++
        }
    }
    return true
}

时间复杂度：$O(n+m)$
空间复杂度：$O(1)$

和为 K 的子数组

560. 和为 K 的子数组 - 力扣（LeetCode）

给定一个整数数组和一个目标值，返回数组中和为目标值的子数组的个数，子数组是数组中元素的连续非空序列

思路：前缀和+哈希

前缀和：对于数组中的任何位置j，前缀和 sum[j] 是数组中从第一个元素到第j个元素的总和，这意味着如果想知道从元素i到j的子数组的和，可以用sum[j] - sum[i]来计算
哈希：用哈希表来存储每个前缀和出现的次数，这是为了快速检查某个特定的前缀和是否已经存在，以及它出现了多少次

核心逻辑：当在数组中向前移动时，逐步增加sum（当前的前缀和）。对于每个新的sum值，我们检查sum - k是否在哈希表中：

sum - k的意义：如果sum - k存在于哈希表中，说明之前在某个点的前缀和是sum - k，由于当前的前缀和是sum，这意味着从那个点到当前点的子数组之和恰好是k，因为sum - (sum - k) = k

如何使用这个信息：如果sum - k在哈希表中，那么sum - k出现的次数表示从不同的起始点到当前点的子数组和为k的不同情况，这是因为每一个sum - k都对应一个起点，使得从那个起点到当前点的子数组和为k

因此，每当找到一个sum - k存在于哈希表中时，就把它的计数（即之前这种情况发生的次数）加到结果上，因为这表示又找到了相应数量的以当前元素结束的子数组，其和为k

例子：假设k = 7，并且当前的前缀和是 10，如果在哈希表中 3（即 10 - 7）出现了两次，这表示存在两个不同的起始点，使得从那些起始点到当前点的子数组之和是 7

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


func subarraySum(nums []int, k int) int {
    res := 0
    // 记录每个前缀和出现次数
    mp := make(map[int]int)
    // 前缀和0初始化次数为1
    mp[0]++
    // 记录前缀和
    sum := 0
    // 遍历数组
    for _, v := range nums {
        // 计算当前前缀和
        sum += v
        // 判断是否存在目标前缀和tar,使得当前前缀和-目标前缀和=k
        if count, ok := mp[sum-k]; ok {
            // 统计结果
            res += count
        }
        // 当前前缀和加入字典
        mp[sum]++
    }
    return res
}

有效的数独

36. 有效的数独 - 力扣（LeetCode）

验证一个已经填入的数字 9 x 9 的数独是否有效

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

思路：每行、每列、每个3×3都用一个哈希表来记录出现过哪些数字，一共9×3个哈希表。哈希表可以有三种表现形式：

map字典
数组
二进制整数：置1时先左移再或，比较时右移再且；例如 ...1110001110 代表数值 [1,3] 和 [7,9] 均被填入。

数组

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


func isValidSudoku(board [][]byte) bool {
    // row[i][j]:第i行的数字j是否存在... area[i][j]:第i个3*3区域的数字j是否存在
    row, col, area := [10][10]bool{}, [10][10]bool{}, [10][10]bool{}
    // 遍历9*9
    for i := range board {
        for j, v := range board[i] {
            // 判当前是否为数字字符
            if board[i][j] != '.' {
                // 数字字符->整型数
                num := v - '0'
                // 判该数字字符是否已存在
                if row[i][num] || col[j][num] || area[i/3*3+j/3][num] {
                    return false
                }
                // 记录该数字
                row[i][num], col[j][num], area[i/3*3+j/3][num] = true, true, true
            }
        }
    }
    return true
}

二进制

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


func isValidSudoku(board [][]byte) bool {
    // row[i]:记录第i行的所有数字存在情况... area[i][j]:记录第i个3*3区域的所有数字存在情况
    row, col, area := [10]int16{}, [10]int16{}, [10]int16{}
    // 遍历9*9
    for i := range board {
        for j, v := range board[i] {
            // 判当前是否为数字字符
            if board[i][j] != '.' {
                // 数字字符->整型数
                num := v - '0'
                // 判该数字字符是否已存在
                if (row[i]>>num)&1 == 1 || (col[j]>>num)&1 == 1 || (area[i/3*3+j/3]>>num)&1 == 1 {
                    return false
                }
                // 记录该数字
                row[i] |= 1 << num
                col[j] |= 1 << num
                area[i/3*3+j/3] |= 1 << num
            }
        }
    }
    return true
}

单词规律

290. 单词规律 - 力扣（LeetCode）

给定一种规律 pattern 和一个字符串 s ，判断 s 是否遵循相同的规律。这里的遵循指完全匹配，例如， pattern 里的每个字母和字符串 s 中的每个非空单词之间存在着双向连接的对应规律。

思路：构建模式串中每个字符与主串中每个单词之间的一一映射关系，比较映射关系是否一致

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


func wordPattern(pattern string, s string) bool {
    // 存储pattern中每个字符与s中每个单词的一一映射关系
    mp1, mp2 := make(map[byte]string), make(map[string]byte)
    // 将s按空格分割为切片
    temp := strings.Split(s, " ")
    // 判模式串与主串长度是否一致
    if len(pattern) != len(temp) {
        return false
    }
    // 遍历模式串 构建一一映射关系并比较是否一致
    for i := 0; i < len(pattern); i++ {
        // 判p->s映射关系是否存在
        if _, ok := mp1[pattern[i]]; !ok {
            mp1[pattern[i]] = temp[i]
        }
        // 判s->p映射关系是否存在
        if _, ok := mp2[temp[i]]; !ok {
            mp2[temp[i]] = pattern[i]
        }
        // 判p<->s一一映射是否成立
        if mp1[pattern[i]] != temp[i] || mp2[temp[i]] != pattern[i] {
            return false
        }
    }
    return true
}

存在重复元素 II

219. 存在重复元素 II - 力扣（LeetCode）

给定一个整数数组 nums 和一个整数 k ，判数组中是否存在俩重复元素，且这俩重复元素索引|idx1-idx2| <= k。如果存在，返回 true ；否则，返回 false

思路一：哈希表+暴力

哈希表记录各数的最大索引，边遍历数组边查找，若遇到相同数字且距离小于等于k，则返回true，否则将当前数字及其索引加入哈希表

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


func containsNearbyDuplicate(nums []int, k int) bool {
    // 记录各数的最大索引
    mp := map[int]int{}
    // 边遍历边查找
    for i, v := range nums {
        // 判是否遇到相同数字
        if idx, ok := mp[v]; ok {
            // 判俩相同数字距离是否小于等于k
            if i-idx <= k {
                return true
            }
        }
        // 更新字典
        mp[v] = i
    }
    return false
}

时间复杂度：$O(n)$
空间复杂度：$O(n)$，最坏情况下，哈希表会记录每个元素的最大下标

思路二：哈希表+滑动窗口

哈希表记录哈希表中存在的数，维护窗口大小不大于k；若窗口大于k，则移出左边界，右边界入窗；若右边界在窗口中有一样的数字，则返回true

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


func containsNearbyDuplicate(nums []int, k int) bool {
    // 记录窗口中存在的数字
    mp := map[int]bool{}
    // 维护大小为k+1窗口
    left := 0
    for right, v := range nums {
        // 判窗口大小是否大于k
        if right-left > k {
            // 移出左边界
            delete(mp, nums[left])
            left++
        }
        // 判右边界数字是否在窗口中存在
        if mp[v] {
            return true
        }
        // 加入右边界
        mp[v] = true
    }
    return false
}

时间复杂度：$O(n)$
空间复杂度：$O(k)$，哈希表只记录滑动窗口中的元素