回溯算法

理论基础

什么是回溯法

回溯法也可以叫做回溯搜索法，它是一种搜索的方式。

回溯是递归的副产品，只要有递归就会有回溯。

回溯函数也就是递归函数

使用原因以及解决的问题

虽然回溯法很难也不好理解，但是回溯法并不是高效的算法。因为回溯的本质是穷举，如果想让回溯法高效一些，可以加一些剪枝的操作。

回溯法并不高效但还要用它是因为一些问题能暴力搜出来就不错了，最多再剪枝一下，还没有更高效的解法。

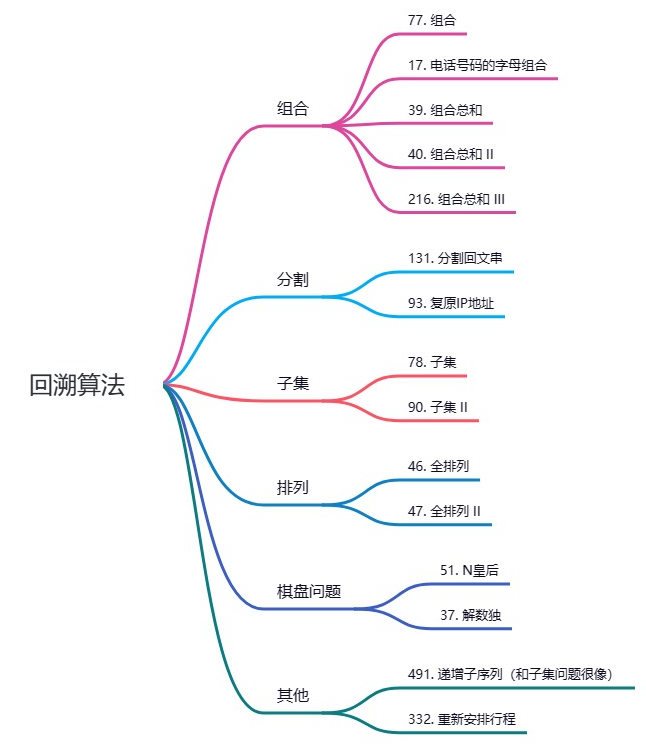
回溯法，一般可以解决如下几种问题：

组合问题：N个数里面按一定规则找出k个数的集合
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个含N个数的集合里有多少符合条件的子集
排列问题：N个数按一定规则全排列，有几种排列方式
棋盘问题：N皇后，解数独

如何理解回溯法

回溯法解决的问题都可以抽象为树形结构

回溯法解决的问题都是在集合中递归查找子集，集合的大小构成了树的宽度，递归的深度构成了树的深度

是递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）

回溯法模板

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

回溯函数函数名、返回值和参数

函数名通常为backtracking
返回值一般为void
参数由函数内逻辑决定

回溯函数终止条件

搜到叶子节点找到了满足条件的一条答案，然后将答案存放起来，并结束本层递归

回溯搜索的遍历过程

回溯法一般是在集合中递归搜索，集合的大小构成了树的宽度，递归的深度构成了树的深度

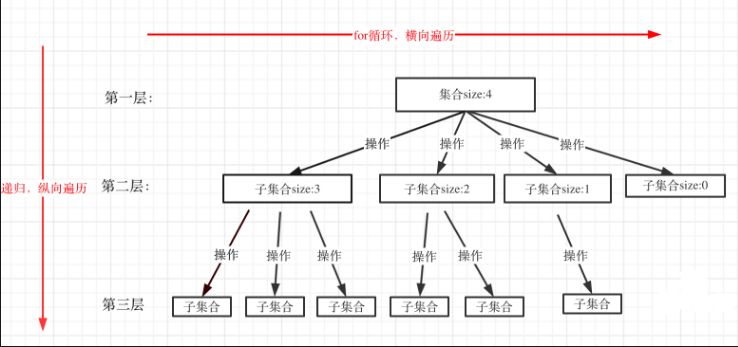
图中举例集合大小和孩子数量相等

每个节点相当于本层的一个for循环

for循环就是遍历集合区间，可以理解一个节点有多少个孩子，这个for循环就执行多少次，backtracking自己调用自己，实现递归

从图中看出for循环是横向遍历，backtracking（递归）是纵向遍历，这样就将这棵树进行了遍历，一般来说，搜索到的叶子节点就是结果

总结

回溯和递归是相辅相成的
回溯法是暴力查找并不高效
回溯法解决的每一类问题都不简单
回溯法解决的问题都可以抽象为树形结构（N叉树）
回溯算法是指数级别的时间复杂度

组合问题

组合

77. 组合 - 力扣（LeetCode）

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

假设输入n=4，k=2，可以把组合问题抽象为如下树形结构；一开始集合是1，2，3，4，从左向右每次取一个数，取过的数不再重复取；第一次取1，下一层集合变为2，3，4 ；因为k为2，所以只需要再取一个数就可以了，分别取2，3，4，得到集合[1,2] [1,3] [1,4]，以此类推

每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围。
图中可以发现n相当于树的宽度，k相当于树的深度。
图中每次搜索到了叶子节点，就找到了一个结果。

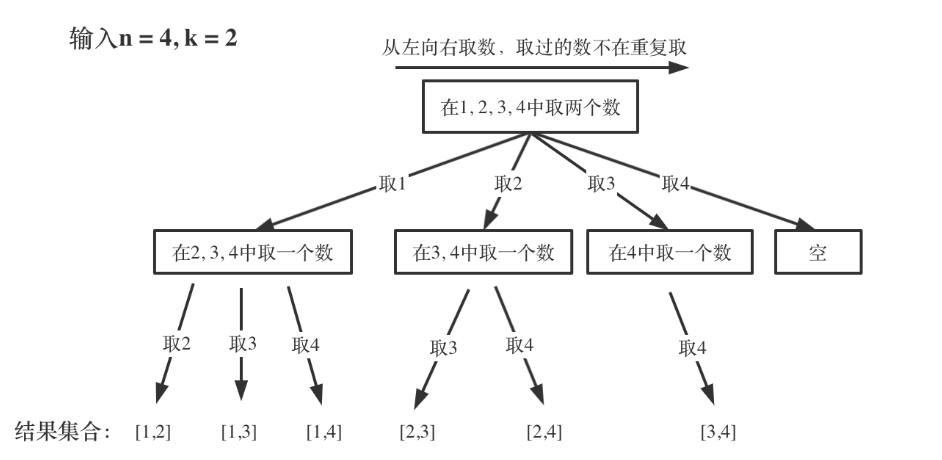
相当于只需要把达到叶子节点的结果收集起来，就可以求得n个数中k个数的组合集合。

递归参数和返回值：参数有题目给定的n和k以及标记本层开始搜索位置的索引；不需要返回值；路径和结果集作为全局变量
终止条件：路径长度等于给定k
单层逻辑：判断路径长度是否等于给定k，若相等说明找到一个结果，收集后返回；进入for循环将本层节点加入路径，然后向深处搜索，由于要保证集合中的数不重复，所以向深递归的参数中下一次搜索开始位置的索引要加一，最后是回溯操作将下一层加入路径的值删除，保证只记录到本层路径值

注意：当剩下的元素不足以填充时进行剪枝，当前元素加一是因为当前元素尚未加入路径；剪枝操作可以在遇到像n=4，k=4这种情况时，剪掉第一层for循环从元素2开始的遍历，剪掉第二层for循环从元素3开始的遍历

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25


var path []int
var res [][]int

func combine(n int, k int) [][]int {
    path = make([]int, 0)
    res = make([][]int, 0)
    backtracking(n, k, 1)
    return res
}
func backtracking(n, k, startIndex int) {
    if len(path) == k { // 找到一个结果
        temp := make([]int, k)
        copy(temp, path)
        res = append(res, temp) // 收集结果
        return
    }
    for i := startIndex; i <= n; i++ { // 遍历本层
        if n-i+1 < k-len(path) { // 剩下的元素不足以填充
            break // 剪枝
        }
        path = append(path, i)    // 当前节点加入路径
        backtracking(n, k, i+1)   // 向深递归
        path = path[:len(path)-1] // 回溯
    }
}

时间复杂度: O(n×2ⁿ)
空间复杂度: O(n)

组合总和III

216. 组合总和 III - 力扣（LeetCode）

用1-9找出和为n的k个数，组合内每个数字只能出现一次，不能有元素相同的组合

先求出组合，然后在存放结果前对组合求和

递归参数和返回值：参数是给定n和k，以及标记本层开始位置的索引和路径和；不需要返回值；路径、结果集是全局变量
终止条件：路径长度等于给定 k
单层逻辑：判断路径长度是否等于给定k，若路径和也等于给定n则加入结果集，最后返回；进入for循环，将当前值加入路径，向深搜索，参数的开始索引加一，回溯操作删除下一层加入路径的节点值

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


var path []int
var res [][]int

func combinationSum3(k int, n int) [][]int {
	path = make([]int, 0)
	res = make([][]int, 0)
	backtracking(k, n, 1, 0)
	return res
}
func backtracking(k, n, startIndex, sum int) {
	if len(path) == k { // 找到满足长度的路径
		if sum == n { // 找到一个目标路径
			temp := make([]int, k)
			copy(temp, path)
			res = append(res, temp) // 收集结果
		}
		return
	}
	for i := startIndex; i <= 9; i++ {
		if sum+i > n || 9-i+1 < k-len(path) { // 剩余元素数不满足所需
			break // 剪枝
		}
		path = append(path, i)         // 当前值记入路径
		backtracking(k, n, i+1, sum+i) // 向深搜索
		path = path[:len(path)-1]      // 回溯
	}
}

时间复杂度: O(n×2ⁿ)
空间复杂度: O(n)

电话号码的字母组合

17. 电话号码的字母组合 - 力扣（LeetCode）

给定一个字符串仅包含数组2-9和一幅图，图中有数字到字母的映射，一个数字可映射为3-4个字母，返回给定字符串中数字可映射的所有字母组合

在多个集合中求组合数（每个集合中取一个元素且不重复），同一集合内元素不构成组合，因为下一层是在下一个集合中取元素，所以不需要在同一集合内去重

递归参数和返回值：参数是给定字符串和本层开始位置的索引；不需要返回值；路径、结果集、映射表是全局变量
终止条件：路径长度等于给定字符串长度
单层逻辑：判断路径长度是否等于字符串长度，若是则收集结果；根据本层开始位置从给定字符串中取出一个字母，再从映射表中查出该字母对应的集合；进入for循环遍历该集合，将当前值加入路径，向深搜索，回溯操作删除下一层加入路径的节点值

注意：

一开始判断给定字符串若为空，直接返回
go中string类型是值类型，深拷贝

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


var path string
var res []string
var mapping = map[byte]string{
    '2': "abc",
    '3': "def",
    '4': "ghi",
    '5': "jkl",
    '6': "mno",
    '7': "pqrs",
    '8': "tuv",
    '9': "wxyz",
}

func letterCombinations(digits string) []string {
    if len(digits) == 0 {
        return []string{}
    }
    path = ""
    res = make([]string, 0)
    backtracking(digits, 0)
    return res
}
func backtracking(digits string, startIndex int) {
    if len(path) == len(digits) {
        temp := path            // 深拷贝
        res = append(res, temp) // 收集结果
        return
    }
    letters := mapping[digits[startIndex]] // 取出一个新集合
    for i := 0; i < len(letters); i++ {    // 遍历新集合
        path += string(letters[i])         // 当前值加入路径
        backtracking(digits, startIndex+1) // 向深搜索
        path = path[:len(path)-1]          // 回溯
    }
}

时间复杂度: O(3^m× 4ⁿ)，其中 m 是对应四个字母的数字个数，n 是对应三个字母的数字个数
空间复杂度: O(3^m × 4ⁿ)

组合总和

39. 组合总和 - 力扣（LeetCode）

给定一个单集合和目标和，组合内元素可以重复选，返回所有是目标和的组合

树中向深搜索时，可以重复；树中向宽搜索时，不能重复

递归参数和返回值：参数是给定数组、目标和、起始索引、路径和；不需要返回值；路径和结果集是全局变量
终止条件：路径和大于等于目标和
单层逻辑：判断路径和是否大于等于目标和，若等于则收集结果，最后返回；进入for循环从起始位置遍历给定数组，将当前值加入路径，向深搜索，回溯删除下一层的路径值

注意：

由于深度搜索可以重复选当前元素，所以起始索引作为参数传递向下一层时不加一，表示仍从当前元素开始；
宽度遍历的不重复由for循环步进保证；宽度遍历下分支的不重复由上一层传入的起始位置保证；
若for循环每次从数组头开始遍历，会导致组合内元素相同而顺序不同的情况出现，原因是宽度遍历后面的分支会使用前面的元素，即宽度遍历的后续分支只有第一层是由for步进控制不重复，下面层会重复选本宽度起始位置之前的元素；而for循环每次从上一层传入的起始位置开始遍历则可以保证本分支始终不会重复使用之前分支的元素

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


var path []int
var res [][]int

func combinationSum(candidates []int, target int) [][]int {
    path, res = make([]int, 0), make([][]int, 0)
    backtracking(candidates, target, 0, 0)
    return res
}
func backtracking(candidates []int, target, startIndex, sum int) {
    if sum >= target { // 路径和大于等于目标和
        if sum == target { // 路径和等于目标和
            temp := make([]int, len(path))
            copy(temp, path)
            res = append(res, temp) // 收集结果
        }
        return
    }
    for i := startIndex; i < len(candidates); i++ {
        path = append(path, candidates[i])                     // 当前节点加入路径
        backtracking(candidates, target, i, sum+candidates[i]) // 向深搜索
        path = path[:len(path)-1]                              // 回溯
    }
}

时间复杂度: O(n × 2ⁿ)
空间复杂度: O(target)

组合总和II

40. 组合总和 II - 力扣（LeetCode）

给定一个单集合和目标和，集合里有重复元素，每个元素在每个组合里只能用一次，不能有重复组合

深逐个遍历；宽逐个遍历但遇到重复要去重，避免重复组合；求出组合后再去重会超出内存限制

先排序，若当前元素与前一个元素相同且是宽度遍历则跳过该元素；因为深度遍历每下一层，i都从startIndex开始，所以判断若i == startIndex，则说明是深遍历；反之，若i != startIndex，则说明是宽遍历

递归参数和返回值：参数是给定数组、目标和、起始位置、路径和；不需要返回值；路径、结果集是全局变量
终止条件：路径和大于等于目标和
单层逻辑：判断路径和是否大于等于目标和，若等于则收集结果，最后返回；进入for循环从起始位置遍历给定数组，若当前元素不是第一个且与前一个元素相同且是宽度遍历，则跳过该元素；将当前值加入路径，向深搜索，回溯

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


var path []int
var res [][]int

func combinationSum2(candidates []int, target int) [][]int {
    path, res = make([]int, 0), make([][]int, 0)
    sort.Ints(candidates)
    backtracing(candidates, target, 0, 0)
    return res
}
func backtracing(candidates []int, target, startIndex, sum int) {
    if sum >= target { // 路径和大于等于目标和
        if sum == target { // 路径和等于目标和
            temp := make([]int, len(path))
            copy(temp, path)
            res = append(res, temp) // 收集结果
        }
        return
    }
    for i := startIndex; i < len(candidates); i++ {
        // 该方式的宽度去重只适用于排序数组
        // 未排序数组宽度去重需要用used哈希表
        if i != startIndex && candidates[i] == candidates[i-1] { // 宽度遍历时遇到重复元素
            continue // 跳过重复元素
        }
        path = append(path, candidates[i])                      // 当前值加入路径
        backtracing(candidates, target, i+1, sum+candidates[i]) // 向深搜索
        path = path[:len(path)-1]                               // 回溯
    }
}

时间复杂度: O(n × 2ⁿ)
空间复杂度: O(n)

分割问题

分割回文串

131. 分割回文串 - 力扣（LeetCode）

给定一个字符串，将其切割为一个或多个子串，保证切割后的子串都是回文串，返回所有切割方案

用startIndex作为子串的起始位置，i表示子串的终止位置；宽度遍历时终止位置i会不断向后移动，深度遍历时起始位置startIndex会不断向后移动；宽度遍历是扩充子串、深度遍历是切割出了一个回文串，继续切出其他子串

递归参数和返回值：参数是给定字符串和起始位置；不需要返回值；路径和结果集是全局变量
终止条件：起始位置到达给定字符串末尾
单层逻辑：判断起始位置是否到达给定字符串末尾，若是则说明找到了一个分割方案，收集结果后返回；进入for循环从起始位置遍历字符串，按照起始位置终止位置切割出子串，若子串是回文串则当前子串加入路径、向深搜索、回溯，若不是则不做操作，宽度遍历下一子串

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39


var path []string
var res [][]string

func partition(s string) [][]string {
    path, res = make([]string, 0), make([][]string, 0)
    backtracking(s, 0)
    return res
}
func backtracking(s string, startIndex int) {
    // 起始位置到分割线末尾
    if startIndex == len(s) {
        // 收集结果
        temp := make([]string, len(path))
        copy(temp, path)
        res = append(res, temp) 
        return
    }
    for i := startIndex; i < len(s); i++ {
        // 切割出子串
        str := s[startIndex:i+1]
        // 判断是否为回文串
        if isHuiWen(str) {
            // 当前子串加入路径
            path = append(path, str)   
            // 向深搜索
            backtracking(s, i+1)     
            // 回溯
            path = path[:len(path)-1]   
        }
    }
}
func isHuiWen(s string) bool {
    for i, j := 0, len(s)-1; i < j; i, j = i+1, j-1 {
        if s[i] != s[j] {
            return false
        }
    }
    return true
}

时间复杂度: O(n × 2ⁿ)
空间复杂度: O(n²)

复原IP地址

93. 复原 IP 地址 - 力扣（LeetCode）

给定一个字符串，请加入三个点，将其分割成四部分表示一个有效得到IP地址，有效 IP 地址正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔

递归参数和返回值：参数是给定字符串、起始索引、点数；不需要返回值；路径、结果集是全局变量
终止条件：点数为三
单层逻辑：判断点数是否为三，若是判断最后一段是否有效，若有效记录该IP，最后返回；进入for循环，以起始索引为起始位置，循环变量i为终止位置分割出子串，判断子串是否有效，若有效则向深搜索，起始位置从上一层的终止位置前进找下一子串，点数加一；回溯

注意：由于终止条件中收集结果前向路径中添加了当前子串，所以收集结果后需要回溯路径

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41


var path string
var res []string

func restoreIpAddresses(s string) []string {
    path = ""
    res = make([]string, 0)
    backtracking(s, 0, 0)
    return res
}
func backtracking(s string, startIndex, pointSum int) {
    if pointSum == 3 { // 已有三个点
        str := s[startIndex:len(s)] // 取最后一段
        if isValid(str) {           // 最后一段有效
            path += str                      // 最后一段加入路径
            res = append(res, path)          // 记录有效IP
            path = path[:len(path)-len(str)] // 回溯
        }
        return
    }
    for i := startIndex; i < len(s); i++ {
        str := s[startIndex : i+1] // 取一段
        if isValid(str) {          // 该段有效
            path += str + "."                  // 当前段加入路径
            backtracking(s, i+1, pointSum+1)   // 向深搜索
            path = path[:len(path)-len(str)-1] // 回溯
        }
    }
}
func isValid(s string) bool {
    if len(s) == 0 { // 空串
        return false
    }
    if len(s) != 1 && s[0] == '0' { // 前导0
        return false
    }
    IntByStr, err := strconv.Atoi(s)
    if err != nil || IntByStr < 0 || IntByStr > 255 { // 无效
        return false
    }
    return true
}

时间复杂度: O(3⁴)，IP地址最多包含4个数字，每个数字最多有3种可能的分割方式，则搜索树的最大深度为4，每个节点最多有3个子节点。
空间复杂度: O(n)

子集问题

子集

78. 子集 - 力扣（LeetCode）

给定一个整数数组，数组中元素互不相同，返回该数组中所有可能的子集

宽遍历不重复，深遍历不重复；搜索过程中的每个路径都是结果集；可以不写终止条件，因为for循环遍历完会自动返回

递归参数和返回值：参数是给定数组、起始位置；不需要返回值；路径、结果集是全局变量
终止条件：不需要显式写出终止条件
单层逻辑：收集结果；进入for循环，当前值加入路径、向深搜索、回溯

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


var path []int
var res [][]int

func subsets(nums []int) [][]int {
    path, res = make([]int, 0), make([][]int, 0)
    backtracking(nums, 0)
    return res
}
func backtracking(nums []int, startIndex int) {
    temp := make([]int, len(path))
    copy(temp, path)
    res = append(res, temp) // 收集结果
    for i := startIndex; i < len(nums); i++ {
        path = append(path, nums[i]) // 当前值加入路径
        backtracking(nums, i+1)      // 向深搜索
        path = path[:len(path)-1]    // 回溯
    }
}

时间复杂度: O(n × 2ⁿ)
空间复杂度: O(n)

子集II

90. 子集 II - 力扣（LeetCode）

给定一个整数数组，数组中可能含有相同元素，返回该数组中所有可能的子集

先排序，遇到和前面元素一样且是宽遍历则跳过该元素

递归参数和返回值：参数是给定数组、起始位置；不需要返回值
终止条件：不需要显式写出终止条件
单层逻辑：收集结果；进入for循环，判断若是宽遍历且与前一个元素相同则跳过该元素、向深搜索、回溯

注意：要先对数组排序，使相同元素相邻

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


var path []int
var res [][]int

func subsetsWithDup(nums []int) [][]int {
    path, res = make([]int, 0), make([][]int, 0)
    sort.Ints(nums)
    backtracking(nums, 0)
    return res
}
func backtracking(nums []int, startIndex int) {
    // 收集结果
    temp := make([]int, len(path))
    copy(temp, path)
    res = append(res, temp) 
    // 遍历
    for i := startIndex; i < len(nums); i++ {
        // 判断是否为宽遍历且与前一个元素相同
        if i != startIndex && nums[i] == nums[i-1] { 
            // 跳过该元素
            continue 
        }
        path = append(path, nums[i]) // 当前值加入路径
        backtracking(nums, i+1)      // 向深搜索
        path = path[:len(path)-1]    // 回溯
    }
}

时间复杂度: O(n × 2ⁿ)
空间复杂度: O(n)

排列问题

全排列

46. 全排列 - 力扣（LeetCode）

给定一个不含重复数字的数组，返回其所有可能的全排列

和求组和的区别是：由于不同排列选取的元素可以相同，所以宽遍历时每次从给定数组的头开始遍历：i=0；由于宽遍历每次从头开始，所以深遍历时需要靠used来记录path中已经存了哪些元素，后面用来去掉同一排列中选取过元素；

used的两种容器：数组、映射；在回溯函数前初始化容器，作为回溯函数的传入参数，需要回溯

递归参数和返回值：参数是给定数组和used；不需要返回值；路径、结果集是全局变量
终止条件：路径长度等于给定数组长度
单层逻辑：判断路径长度是否等于给定数组长度，若是则收集结果并返回；进入for循环，判断该元素在本排列中是否已用过，若用过则跳过元素、当前值加入路径和used、向深搜索、回溯

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


var path []int
var res [][]int

func permute(nums []int) [][]int {
    path, res = make([]int, 0), make([][]int, 0)
    used := make([]bool, len(nums))
    backtracking(nums, used)
    return res
}
func backtracking(nums []int, used []bool) {
    if len(path) == len(nums) {
        temp := make([]int, len(path))
        copy(temp, path)
        res = append(res, temp) // 收集结果
        return
    }
    for i := 0; i < len(nums); i++ {
        if used[i] { // 该排列中使用过该元素
            continue // 跳过该元素
        }
        path = append(path, nums[i]) // 当前值加入路径
        used[i] = true               // 标记该元素使用过
        backtracking(nums, used)     // 向深搜索
        used[i] = false              // 回溯
        path = path[:len(path)-1]    // 回溯
    }
}

时间复杂度: O(n!)
空间复杂度: O(n)

全排列II

47. 全排列 II - 力扣（LeetCode）

给定一个含重复数字的数组，返回其所有可能的全排列

深度遍历可以选相同值的数字，宽度遍历不能选相同值的数字

先排序；宽度遍历时遇到和前一个元素相同且前一个元素没有被使用过（树层去重）则跳过该元素

used[i] == used[i-1] && used[i - 1] == true，说明同一树枝使用过该元素值
used[i] == used[i-1] && used[i - 1] == false，说明同一树层使用过该元素值

注意：不能用映射！因为映射是用元素值作为key，如果遇到重复元素，会覆盖前一个元素的标记；排列问题，树层去重和树枝去重都可以，但是树层去重效率更高

递归参数和返回值：参数是给定数组和used；不需要返回值；路径和结果集是全局变量
终止条件：路径长度等于给定数组长度
单层逻辑：判断路径长度是否等于给定数组长度，若是则收集结果并返回；进入for循环，判断该元素在该排列中是否使用过，若是用过则跳过该元素，判断同一树层是否使用过该元素，若是则跳过，当前值加入路径、向深搜索、回溯

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31


var path []int
var res [][]int

func permuteUnique(nums []int) [][]int {
    path, res = make([]int, 0), make([][]int, 0)
    used := make([]bool, len(nums))
    sort.Ints(nums)
    backtracking(nums, used)
    return res
}
func backtracking(nums []int, used []bool) {
    if len(nums) == len(path) {
        temp := make([]int, len(path))
        copy(temp, path)
        res = append(res, temp) // 收集结果
        return
    }
    for i := 0; i < len(nums); i++ {
        if used[i] { // 该元素在该排列中用过
            continue
        }
        if i != 0 && nums[i] == nums[i-1] && used[i-1] == false { // 宽度遍历遇到重复元素且同层用过
            continue
        }
        path = append(path, nums[i]) // 当前值加入路径
        used[i] = true               // 标记该元素本排列已用过
        backtracking(nums, used)     // 向深搜索
        used[i] = false              // 回溯
        path = path[:len(path)-1]    // 回溯
    }
}

时间复杂度: O(n! × n)
空间复杂度: O(n)

字符串的排列⚫

JZ38 字符串的排列_牛客题霸_牛客网

同上，将数字换成了字符

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


func Permutation(str string) []string {
    strByte := []byte(str)
    sort.Slice(strByte, func(i, j int) bool {
        return strByte[i] < strByte[j]
    })
    res := []string{}
    used := make([]bool, len(str))
    path := []byte{}
    var backTracking func()
    backTracking = func() {
        if len(path) == len(strByte) {
            res = append(res, string(path))
            return
        }
        for i := 0; i < len(strByte); i++ {
            // 判当前字符是否已用过
            if used[i] {
                continue
            }
            // 判宽度遍历是否遇到同值重复字符
            if i != 0 && strByte[i] == strByte[i-1] && used[i-1] {
                continue
            }
            used[i] = true
            path = append(path, strByte[i])
            backTracking()
            used[i] = false
            path = path[:len(path)-1]
        }
    }
    backTracking()
    return res
}

棋盘问题

N皇后

51. N 皇后 - 力扣（LeetCode）

给定一个整数n，返回在n×n棋盘上n个皇后的所有放置方案；皇后可以攻击同行同列同斜线，要求n个皇后互相攻击不到

宽度遍历行；深度遍历列；处理节点、递归、回溯都建立在找到有效位的前提下

宽度遍历时遇到有效位，放置后直接进入下一层遍历下一排（递归），否则就继续宽度遍历（不递归）
宽度遍历递归到叶子节点说明是一个解，收集后回到上一层，继续执行上一层后面的回溯语句来移除放置，寻找下一个可能的解

判断是否为有效位

不用检查行，因为一旦在一行放置后立马会递归到下一层，最终到叶子节点存放结果，然后会回到上一层，执行后续回溯语句，移除放置
检查斜线时，只需检查所在行上面的斜线，因为下面一定是空，还没递归到下面
- 检查上左斜线：用所在行的上一个位置作为排数，所在列的前一个位置作为列数来定位左斜线元素，然后行列递减
- 检查上右斜线：用所在行的上一个位置作为排数，所在列的后一个位置作为列数来定位右斜线元素，然后行递减，列递增

递归三部曲

递归参数和返回值：参数是棋盘、n、当前所在排数；不需要返回值；棋盘和结果集是全局变量
终止条件：排数等于n
单层逻辑：判断当前所在排数是否等于n，若是则收集结果后返回；进入for循环，判断该位置是否有效，若有效则在该位置放置Q、向深搜索、回溯

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51


var chessboard []string
var res [][]string

func solveNQueens(n int) [][]string {
    chessboard, res = make([]string, n), make([][]string, 0)
    tempRow := ""
    for i := 0; i < n; i++ {
        tempRow += "." // 初始化棋盘排
    }
    for i := 0; i < n; i++ {
        chessboard[i] = tempRow // 初始化棋盘每个位置都为空
    }
    backtracking(chessboard, n, 0)
    return res
}
func backtracking(chessboard []string, n int, row int) {
    if row == n {
        temp := make([]string, n)
        copy(temp, chessboard)
        res = append(res, temp) // 收集结果
        return
    }
    for i := 0; i < n; i++ {
        if isValid(chessboard, n, row, i) { // 该位置有效
            tempRow := []byte(chessboard[row]) // 从棋盘中取出该行
            tempRow[i] = 'Q'                   // 放置皇后
            chessboard[row] = string(tempRow)  // 更新棋盘该行
            backtracking(chessboard, n, row+1) // 向深搜索
            tempRow[i] = '.'                   // 回溯
            chessboard[row] = string(tempRow)  // 更新棋盘该行
        }
    }
}
func isValid(chessboard []string, n, row, col int) bool {
    for i := 0; i < n; i++ { // 检查该列
        if chessboard[i][col] == 'Q' {
            return false
        }
    }
    for i, j := row-1, col-1; i >= 0 && j >= 0; i, j = i-1, j-1 {
        if chessboard[i][j] == 'Q' { // 检查上左斜线
            return false
        }
    }
    for i, j := row-1, col+1; i >= 0 && j < n; i, j = i-1, j+1 {
        if chessboard[i][j] == 'Q' { // 检查上右斜线
            return false
        }
    }
    return true
}

时间复杂度: O(n!)
空间复杂度: O(n)

解数独

37. 解数独 - 力扣（LeetCode）

给定一个9×9的棋盘，棋盘中已有一些数字，无数字的用.表示；现在需要用数字1-9填满棋盘，要求每行、每列、每个3×3小宫格内不能出现重复数字

解数独不像N皇后问题，在宽遍历时遇到有效就递归进入下一层，直到叶子节点收集结果，最后回溯，暴力搜出所有结果；解数独在宽遍历遇到有效位时还需要处理该行后续位置，如何在此情况下递归和回溯？由于解数独只有一个结果，填满就返回，所以需要返回值作为成功标志一层层向上返回结束本算法

二维递归，两层for循环，外层定行数，内层定列数，遍历棋盘；对每个位置遍历数字1-9，如果能成功放置，就进入下层递归，重新开始遍历新棋盘填充下一个位置，直至最后一次递归填完所有空返回true；如果遍历完九个数字都不能填入，则返回false，不进入下次递归，证明这次递归填的数有问题，向上回溯还原后，再继续填下一个空，套娃到结束

递归参数和返回值：参数是给定棋盘；返回值是当前位置是否填充成功
终止条件：不需要终止条件，遍历整个树形结构
单层逻辑：两层for循环遍历棋盘，遇到空位置则遍历9个数字判断满足规则后填入，向深递归重新遍历棋盘，接收返回值，若返回值为真说明填完棋盘，直接返回，若返回值为假说明该位置填入的数不对，回溯该位置为空；若遍历完9个数都不能填入，说明之前填入的有误，返回假

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40


func solveSudoku(board [][]byte) {
    backtracking(board)
}
func backtracking(board [][]byte) bool {
    for i := 0; i < 9; i++ { // 行
        for j := 0; j < 9; j++ { // 列
            if board[i][j] == '.' { // 空位置
                for v := 1; v <= 9; v++ { // 遍历9个数
                    if isValid(board, i, j, v) { // 该数有效
                        board[i][j] = uint8(v) + '0' // 填入该数
                        res := backtracking(board)   // 向深搜索
                        if res {                     // 棋盘填充完成
                            return true // 逐层返回
                        }
                        board[i][j] = '.' // 回溯
                    }
                }
                return false // 遍历完9个数都无法填入该位置
            }
        }
    }
    return true // 程序不会执行至此
}
func isValid(board [][]byte, row, col, v int) bool {
    for i := 0; i < 9; i++ { // 检查行列
        if board[i][col] == uint8(v)+'0' || board[row][i] == uint8(v)+'0' {
            return false
        }
    }
    startRow, startCol := row/3*3, col/3*3
    endRow, endCol := startRow+3, startCol+3
    for i := startRow; i < endRow; i++ { // 3×3宫内行
        for j := startCol; j < endCol; j++ { // 3×3宫内列
            if board[i][j] == uint8(v)+'0' {
                return false
            }
        }
    }
    return true
}

其他问题

非递减子序列

491. 非递减子序列 - 力扣（LeetCode）

给定一个整数数组，返回所有的递增子序列，最小长度为2，相同元素视作递增；子序列：不能排序，遵循给定序列的顺序

宽和深遍历都不重复；宽度遍历时遇到重复元素值则跳过该元素；宽和深遍历时遇到比最后一个路径值小的元素则跳过该元素；宽度遍历时遇到重复元素值 => 因为used是每层重新初始化，所以如果used有值说明一定是在宽遍历时遇到重复元素值；路径大于1时收集结果

注意：由于给定数组不是单调的，也不能排序，所以判断宽遍历是否遇到重复元素值要用used数组记录本数层用过的元素；由于是标记元素值是否使用，所以用map

递归参数和返回值：参数是给定数组、起始位置；不需要返回值；路径和结果集是全局变量
终止条件：路径长度大于1
单层逻辑：判断路径长度是否大于1，若是则收集结果，不返回；初始化used记录本层元素值使用情况，进入for循环，判断是否宽遍历遇到重复值或当前值小于路径中最后一个值，若是则跳过该元素、将当前值加入路径、标记该元素值已使用、向深搜索、回溯

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


var path []int
var res [][]int

func findSubsequences(nums []int) [][]int {
    path, res = make([]int, 0), make([][]int, 0)
    backtracking(nums, 0)
    return res
}
func backtracking(nums []int, startIndex int) {
    if len(path) > 1 {
        temp := make([]int, len(path))
        copy(temp, path)
        res = append(res, temp) // 收集结果
    }
    // 标记本层用过(遍历过)的元素
    used := make(map[int]bool)
    for i := startIndex; i < len(nums); i++ {
        if used[nums[i]] || (len(path) > 0 && nums[i] < path[len(path)-1]) {
            continue // 宽遍历遇到重复元素值或当前值小于路径中最小值
        }
        path = append(path, nums[i]) // 当前值加入路径
        used[nums[i]] = true         // 标记本层该值使用过
        backtracking(nums, i+1)      // 向深搜索
        path = path[:len(path)-1]    // 回溯
        // used不用回溯 因为用过（遍历过）
    }
}

时间复杂度: O(n × 2ⁿ)
空间复杂度: O(n)

重新安排行程

332. 重新安排行程 - 力扣（LeetCode）

给定一个二维字符数组，每个一维数组长度为2，表示元素0到元素1的一张机票；现在对所有航线重新排序，要求从JFK出发，方案字典值最小

用一个map存航线信息，key表示出发地，value是一个字符数组，表示该出发地能到达的降落地，降落地按字典值升序排列；从JFK开始，取出一个降落地作为降落地和新的出发地，然后从字典中删除该降落地，用新出发地向深搜索，直到字典中没有该出发地对应的值，说明找到最后一个降落地，向上边回溯边由后向前拼接出航线

递归参数和返回值：参数是起始地；不需要返回值；航班信息、结果集是全局变量
终止条件：不需要终止条件，找到航线逐层回溯返回
单层逻辑：若字典中该出发地的对应的降落地不为空，则进入for循环，从字典中查出该出发地对应的第一个降落地，删除该降落地，以该降落地为出发地向深搜索；最后跳出for循环则说明找到目标航线，将本层的出发地拼接到结果集前面

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


var mp map[string][]string
var res []string

func findItinerary(tickets [][]string) []string {
    mp, res = make(map[string][]string), make([]string, 0)
    for _, v := range tickets { // 遍历航线
        mp[v[0]] = append(mp[v[0]], v[1]) // 邻接表方式将航线信息存入字典
    }
    for _, v := range mp { // 遍历字典
        sort.Strings(v) // 对值(降落地)升序排序
    }
    backtracking("JFK")
    return res
}

func backtracking(start string) {
    for len(mp[start]) > 0 { // 该出发地有降落地
        end := mp[start][0]       // 取出字典值最小的一个降落地
        mp[start] = mp[start][1:] // 在邻接表中删除该降落地
        backtracking(end)         // 向深搜索
    }
    res = append([]string{start}, res...) // 回溯并逐层拼接结果集
}

括号生成

22. 括号生成 - 力扣（LeetCode）

数字 n 代表生成括号的对数，设计一个函数，用于能够生成所有可能的并且 有效的 括号组合

思路

不停选括号，要么选左括号，要么选右括号。有这些约束：

只要选中的左不够n时，就可以选左
当左比右多时，就可以选右

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


func generateParenthesis(n int) []string {
    res, path := make([]string, 0), make([]byte, 2*n)
    var backtracking func(int, int, int)
    backtracking = func(cnt, lCount, rCount int) {
        // 判断当前括号数是否达标
        if cnt == 2*n {
            res = append(res, string(path))
            return
        }
        // 判断当前左括号数是否未到最大值
        if lCount < n {
            path[cnt] = '('
            backtracking(cnt+1, lCount+1, rCount)
        }
        // 判断当前左括号数是否多于右括号数
        if lCount > rCount {
            path[cnt] = ')'
            backtracking(cnt+1, lCount, rCount+1)
        }
    }
    backtracking(0, 0, 0)
    return res
}

单词搜索

79. 单词搜索 - 力扣（LeetCode）

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

思路：

定义dfs(i, j, k)表示当前在board[i][j]这个格子，要匹配word[k]，返回在这个状态下最终能否匹配成功（搜索成功）

分类讨论：

如果 board[i][j] = word[k]，匹配失败，返回false
否则，如果 k = len(word)−1，匹配成功，返回true
否则，枚举 (i,j) 周围的四个相邻格子(x,y)，如果(x,y)没有出界，则递归 dfs(x, y, k+1)，如果其返回true，则 dfs(i, j, k) 也返回true。
如果递归周围的四个相邻格子都没有返回 true，则最后返回 false，表示没有搜到

细节：

递归过程中，为了避免重复访问同一个格子，可以用 visited 数组标记。更简单的做法是，直接修改 board[i][j]，将其置为空（或者 0），返回 false 前再恢复成原来的值（恢复现场）。注意返回 true 的时候就不用恢复现场了，因为已经成功搜到 word 了

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64


func exist(board [][]byte, word string) bool {
    // 优化一
    // 统计board中各字符个数
    cnt := make(map[byte]int)
    for i := range board {
        for j := range board[i] {
            cnt[board[i][j]]++
        }
    }
    // 统计word中各字符个数同时判断是否超过board中该字符个数
    wordB := []byte(word)
    wordCnt := make(map[byte]int)
    for _, ch := range wordB {
        wordCnt[ch]++
        // 判断word中该字符个数是否超过board中该字符个数
        if wordCnt[ch] > cnt[ch] {
            // 无法找到
            return false
        }
    }
    // 优化二
    // 判断word末字符个数是否多于首字符个数
    if cnt[wordB[len(wordB)-1]] > cnt[wordB[0]] {
        // 反转word
        slices.Reverse([]byte(wordB))
    }
    // dfs回溯
    direction := [][]int{{1, 0}, {-1, 0}, {0, 1}, {0, -1}}
    var dfs func(int, int, int) bool
    dfs = func(i, j, curIdx int) bool {
        // 判断当前字符是否匹配
        if board[i][j] != wordB[curIdx] {
            return false
        }
        // 判断是否匹配到最后一个字符
        if curIdx == len(wordB)-1 {
            return true
        }
        // 标记当前字符访问过
        board[i][j] = 0
        // 遍历四个方向
        for _, offset := range direction {
            x, y := i+offset[0], j+offset[1]
            // 向深搜索
            if x >= 0 && y >= 0 && x < len(board) && y < len(board[0]) && dfs(x, y, curIdx+1) {
                // 搜到了
                return true
            }
        }
        // 回溯
        board[i][j] = wordB[curIdx]
        // 没找到
        return false
    }
    for i := range board {
        for j := range board[i] {
            if dfs(i, j, 0) {
                // 搜到了
                return true
            }
        }
    }
    return false
}

删除无效的括号

301. 删除无效的括号 - 力扣（LeetCode）

给定一个由若干括号和字母组成的字符串 s ，删除最小数量的无效括号，使得输入的字符串有效。返回所有可能的结果。答案可以按 任意顺序 返回

思路：回溯+剪枝

递归参数和返回值：参数是当前字符串、起始位置，剩余需删除的左右括号数；不需要返回值
终止条件：要删除的最少左右括号数都用完
单层逻辑：
- 若要删除的最少左右括号数都用完，则判当前字符串是否有效，若有效则收集结果，最后返回上一层；
- 从起始位置开始遍历到当前字符串结束
  - 若当前字符与前一字符相同，则跳过本字符，继续向后搜索不同字符（宽度遍历不重复）；
  - 若剩余字符不足以删除最少括号数则直接返回上一层；
  - 若当前字符为左括号且仍需要删除左括号，则将删除该左括号后的字符串作为回溯函数的参数，向深搜索，同时更新需删除的左括号数
  - 右括号同理

统计「左括号」和「右括号」各自最少应该删除的数量

遍历一遍字符串

当遍历到「左括号」的时候，「左括号」数量加 1
当遍历到「右括号」的时候：
- 若此时「左括号」的数量不为 0，因为「右括号」可以与之前遍历到的「左括号」匹配，此时「左括号」出现的次数 −1；
- 若此时「左括号」的数量为 0，「右括号」数量加 1

判字符串是否有效

遍历当前字符串，统计左右括号抵消后的数量，若出现负数，说明该右括号之前无左括号可供匹配，此为无效字符串

当遍历到「左括号」的时候，计数加 1，当遍历到「右括号」的时候，计数减 1
当计数为负，则无效，若能全部遍历且最终计数为0，则有效

剪枝

从字符串中每去掉一个括号，则更新 lremove 或者 rremove，当发现剩余未尝试的字符串的长度小于 lremove+rremove 时，则停止本次搜索
当 lremove 和 rremove 同时为 0 时，则检测当前的字符串是否合法匹配，如果合法匹配则将其记录下来

去重

利用哈希表对最终生成的字符串去重
在每次进行搜索时，如果遇到连续相同的括号只需要搜索一次即可，比如当前遇到的字符串为 (((())，去掉前四个左括号中的任意一个，生成的字符串是一样的，均为 ((())，因此在尝试搜索时，只需去掉一个左括号进行下一轮搜索，不需要将前四个左括号都尝试一遍

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131


func removeInvalidParentheses(s string) []string {
    // 遍历字符串分别统计左右括号最少删除数
    lremove, rremove := 0, 0
    for _, ch := range s {
        if ch == '(' {
            lremove++
        } else if ch == ')' {
            if lremove == 0 {
                rremove++
            } else {
                lremove--
            }
        }
    }
    res := make([]string, 0)
    var backtracking func(string, int, int, int)
    backtracking = func(s string, startIdx, lremove, rremove int) {
        // 判要删除的左右括号数是否用完
        if lremove == 0 && rremove == 0 {
            // 判当前字符串是否有效
            if isValid(s) {
                // 收集结果
                res = append(res, s)
            }
            return
        }
        // 遍历当前字符串
        for i := startIdx; i < len(s); i++ {
            // 去重 宽度遍历不重复 相同字符只用第一个
            if i != 0 && s[i] == s[i-1] {
                continue
            }
            // 剪枝 判当前剩余字符数是否够删
            if lremove+rremove > len(s)-i {
                // 不够删直接返回上一层
                return
            }
            // 删除当前字符串(左括号)
            if lremove > 0 && s[i] == '(' {
                backtracking(s[:i]+s[i+1:], i, lremove-1, rremove)
            }
            // 删除当前字符串(右括号)
            if rremove > 0 && s[i] == ')' {
                backtracking(s[:i]+s[i+1:], i, lremove, rremove-1)
            }
        }
    }
    // 回溯遍历所有方案
    backtracking(s, 0, lremove, rremove)
    return res
}
func isValid(s string) bool {
    cnt := 0
    // 遍历字符串
    for _, ch := range s {
        if ch == '(' {
            cnt++
        } else if ch == ')' {
            cnt--
            // 若有右括号无法被匹配则直接返回false
            if cnt < 0 {
                return false
            }
        }
    }
    // 若所有括号都成功匹配则返回true
    return cnt == 0
}
// 写法二
func removeInvalidParentheses(s string) []string {
    // 统计左右括号需删除的个数
    lremove, rremove := 0, 0
    for _, ch := range s {
        if ch == '(' {
            lremove++
        } else if ch == ')' {
            if lremove > 0 {
                lremove--
            } else {
                rremove++
            }
        }
    }
    res := []string{}
    // 回溯
    var backtracking func(string, int)
    backtracking = func(s string, startIdx int) {
        if lremove == 0 && rremove == 0 {
            if isValid(s) {
                res = append(res, s)
            }
            return
        }
        // 剪枝
        if lremove+rremove > len(s)-startIdx {
            return
        }
        for i := startIdx; i < len(s); i++ {
            // 宽度遍历去重
            if i != startIdx && s[i] == s[i-1] {
                continue
            }
            if lremove > 0 && s[i] == '(' {
                lremove--
                backtracking(s[:i]+s[i+1:], i)
                lremove++
            }
            if rremove > 0 && s[i] == ')' {
                rremove--
                backtracking(s[:i]+s[i+1:], i)
                rremove++
            }
        }
    }
    backtracking(s, 0)
    return res
}
func isValid(s string) bool {
    cnt := 0
    for _, ch := range s {
        if ch == '(' {
            cnt++
        } else if ch == ')' {
            if cnt <= 0 {
                return false
            }
            cnt--
        }
    }
    return true
}

时间复杂度：O(n×2^n)，其中 n 为字符串的长度。考虑到一个字符串最多可能有 2^n个子序列，每个子序列可能需要进行一次合法性检测，因此时间复杂度为 O(n×2^n)
空间复杂度：O(n^2)，其中 n 为字符串的长度。返回结果不计入空间复杂度，考虑到递归调用栈的深度，并且每次递归调用时需要复制字符串一次，因此空间复杂度为 O(n^2)

排列序列

60. 排列序列 - 力扣（LeetCode）

给出集合 [1,2,3,...,n]，其所有元素共有 n! 种排列。给定 n 和 k，返回第 k 个排列。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60


func getPermutation(n int, k int) string {
    res := []string{}
    path := []byte{}
    mp := map[int]bool{}
    var backtracking func()
        backtracking = func() {
        if len(res) == k {
            return
        }
        if len(path) == n {
            res = append(res, string(path))
                return
        }
        for i := 1; i <= n; i++ {
            if !mp[i] {
                mp[i] = true
                    path = append(path, byte(i)+'0')
                    backtracking()
                    path = path[:len(path)-1]
                    mp[i] = false
            }
        }
    }
    backtracking()
        return res[k-1]
}

// 写法二
func getPermutation(n int, k int) string {
    res := ""
    path := []int{}
    // 记录本排列用过的元素
    used := map[int]bool{}
    var backtracking func()
        backtracking = func() {
        if k == 0 {
            return
        }
        if len(path) == n {
            k--
                if k == 0 {
                    for _, v := range path {
                        res += strconv.Itoa(v)
                    }
                }
            return
        }
        for i := 1; i <= n; i++ {
            if !used[i] {
                path = append(path, i)
                    used[i] = true
                    backtracking()
                    used[i] = false
                    path = path[:len(path)-1]
            }
        }
    }
    backtracking()
    return res
}