反转字符串
344. 反转字符串 - 力扣(LeetCode)
将输入的字符串反转,要求不给另外的数组分配额外的空间,必须原地修改输入数组、使用O(1)的额外空间解决这一问题
双指针:指向首尾,每次交换,同时移动,直至相遇
1
2
3
4
5
6
7
8
|
func reverseString(s []byte) {
idx1, idx2 := 0, len(s)-1 // 俩指针分别指向首尾
for idx1 < idx2 {
s[idx1], s[idx2] = s[idx2], s[idx1] // 交换值
idx1++ // 后移
idx2-- // 前移
}
}
|
反转字符串 II
541. 反转字符串 II - 力扣(LeetCode)
给定一个字符串 s 和一个整数 k,从字符串开头算起,每计数至 2k 个字符,就反转这 2k 字符中的前 k 个字符。
- 如果剩余字符少于
k 个,则将剩余字符全部反转。
- 如果剩余字符小于
2k 但大于或等于 k 个,则反转前 k 个字符,其余字符保持原样
双指针:快指针遍历字符串,当快指针计数至2k或结束,慢指针指向这2k个字符的开头或剩余字符的开头,反转后,更新慢指针
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
func reverseStr(s string, k int) string {
slowIdx := 0 // 慢指针指向首
sArr := []byte(s) // 字符串转为字符数组
for fastIdx := 0; fastIdx < len(sArr); fastIdx++ { // 快指针遍历数组
if (fastIdx+1)%(2*k) == 0 { // 计数至2k个字符
reverse(sArr[slowIdx : slowIdx+k]) // 反转这2k字符中的前k个字符
slowIdx = fastIdx + 1 // 更新慢指针
}
}
if len(sArr)-slowIdx < k { // 剩余字符少于k个
reverse(sArr[slowIdx:]) // 反转剩余全部字符
} else if len(sArr)-slowIdx >= k && len(sArr)-slowIdx < 2*k { // 剩余字符少于2k但大于或等于k个
reverse(sArr[slowIdx : slowIdx+k]) // 反转前k个字符
}
return string(sArr)
}
// 反转给定的字符串
func reverse(s []byte) {
idx1, idx2 := 0, len(s)-1 // 俩指针分别指向首尾
for idx1 < idx2 {
s[idx1], s[idx2] = s[idx2], s[idx1] // 交换值
idx1++ // 后移
idx2-- // 前移
}
}
|
优化:遍历字符串时每次前进2*k个字符,也就是到了下一个2k的第一个字符;进入循环后判断当前2k的第一个字符加上k个字符后是否超过数组长度,若没超过,则反转i开始的前k个字符,若超过了,反转i开始的全部字符
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
func reverseStr(s string, k int) string {
sArr := []byte(s) // 将字符串转为字符数组
for i := 0; i < len(sArr); i += 2 * k { // 步进2*k
if i+k <= len(sArr) { // i加上k个字符后没超过数组长度
reverse(sArr[i : i+k]) // 反转i开始前k个字符
} else { // i加上k个字符后超过数组长度
reverse(sArr[i:]) // 反转i开始全部字符
}
}
return string(sArr)
}
func reverse(s []byte) {
idx1, idx2 := 0, len(s)-1
for idx1 < idx2 {
s[idx1], s[idx2] = s[idx2], s[idx1]
idx1++
idx2--
}
}
|
替换数字⚫
54. 替换数字(第八期模拟笔试) (kamacoder.com)
给定一个字符串,包含小写字母和数字字符,要求将每个数字字符替换为number
开辟一个新的空间,遍历给定字符串,遇到字母就存入结果集,遇到数字就将number存入结果集
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
package main
import "fmt"
func main() {
var strByte []byte
fmt.Scanln(&strByte)
res := ""
for _, v := range strByte { // 遍历字符串
if v >= 'a' && v <= 'z' { // 遍历到小写字母
res += string(v) // 追加到结果集
} else { // 遍历到数字字符
res += "number"
}
}
fmt.Println(res)
}
|
反转字符串中的单词
151. 反转字符串中的单词 - 力扣(LeetCode)
JZ73 翻转单词序列_牛客题霸_牛客网
给定一个字符串,用空格分隔字符串中的单词,给定的字符串中可能有前导空格、尾随空格或者单词间的多个空格。返回反转单词后的字符串,且单词间应当仅用单个空格分隔也不包含任何额外的空格
思路:双指针:快指针从右向左倒序遍历给定字符串,一对快慢指针确定一个单词;当快指针遇到非空格字符且慢指针指向空格时,说明找到一个单词的尾,此时更新慢指针,用慢指针标记单词尾;当快指针遇到空格字符且慢指针指向非空格字符时,说明快指针遍历完了一个单词,将该单词存入结果集,更新慢指针指向当前快指针(空格),继续找下一单词;最后判断字符串首是否还有最后一个单词
注意:
- 当字符串首字符非空格时,快指针会因为无法遍历到空格从而记录不到首单词,因此要将首字符的单词判断存在后加入
s 包含英文大小写字母、数字和空格 ' ',数字也算单词- 在ASCII中0值最小,z值最大,0~z中包括所有大小写字符且不含空格,有特殊字符,但题目中说明不含特殊字符
- golang的字符串是不可修改的,不存在原地解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
func reverseWords(s string) string {
res := []byte{}
// 慢指针初始指向末尾
slow := len(s) - 1
// 快指针倒序遍历字符串
for fast := len(s) - 1; fast >= 0; fast-- {
// 判快指针是否遇到单词尾
if s[fast] != ' ' && s[slow] == ' ' {
// 更新慢指针指向单词尾
slow = fast
} else if s[fast] == ' ' && s[slow] != ' ' {
// fast遍历到单词首
// 当前单词追加到结果集
res = append(res, []byte(s[fast:slow+1])...)
// 更新慢指针指向空格
slow = fast
}
}
// 判是否存在首字符的单词
if s[0] != ' ' {
res = append(res, ' ')
res = append(res, []byte(s[:slow+1])...)
}
// 去除首空格后返回
return string(res[1:])
}
|
右旋字符串⚫
55. 右旋字符串(第八期模拟笔试) (kamacoder.com)
给定一个字符串和一个整数k,将字符串尾部k个字符移动到字符串首
先选定要移动的子串,然后字符串后移k个单位,再将选定子串放入字符串首
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
package main
import "fmt"
func main() {
var k int
fmt.Scanln(&k)
var s []byte
fmt.Scanln(&s)
temp := make([]byte, k)
copy(temp, s[len(s)-k:len(s)]) // 保存要移动的子串
for i := len(s) - 1; i >= k; i-- { // 字符后移
s[i] = s[i-k]
}
for i := 0; i < k; i++ {
s[i] = temp[i]
}
fmt.Println(string(s))
}
|
找出字符串中第一个匹配项的下标
28. 找出字符串中第一个匹配项的下标 - 力扣(LeetCode)
给定两个字符串,找出第二个字符串在第一个字符串中的下标,若没有则返回-1
思路一:暴力,外层遍历第一个字符串,若遇到字符与第二个字符串首字符相同,则继续比较后续字符,若遇到不一样的,则进入下一外层循环,若外层遍历结束仍未找到,返回-1
写法一(推荐)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
func strStr(haystack string, needle string) int {
i, j := 0, 0
for ; i <= len(haystack)-len(needle); i++ {
for j = 0; j < len(needle); j++ {
if haystack[i+j] != needle[j] {
break
}
}
if j == len(needle) {
return i
}
}
return -1
}
|
写法二
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
func strStr(haystack string, needle string) int {
for i := 0; i <= len(haystack)-len(needle); i++ {
if haystack[i] == needle[0] { // 首字符相同
idx := i // 初始化指针指向字符串1的i
isOk := true // 默认匹配
for j := 0; j < len(needle); j, idx = j+1, idx+1 {
if haystack[idx] != needle[j] {
isOk = false // 不匹配
break
}
}
if isOk {
return i // 返回下标
}
}
}
return -1
}
|
- 时间复杂度:O(n × m)
- 空间复杂度:O(1)
思路二:KMP
该讲解更易理解:https://leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/solutions/575568/shua-chuan-lc-shuang-bai-po-su-jie-fa-km-tb86
KMP,在一个串中查找是否出现过另一个串
KMP的经典思想就是:
- 当出现字符串不匹配时,可以记录一部分之前已经匹配的文本内容,利用这些信息避免从头再去做匹配。
next数组用来记录已经匹配的文本内容,是KMP的重点。next数组就是一个前缀表(prefix table),前缀表是用来回退的,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配
为了清楚了解前缀表的作用,举一个例子:
要在主串 aabaabaafa 中查找是否出现过一个模式串 aabaaf。主串中第六个字符 b 和模式串的第六个字符 f 不匹配了。
- 如果是暴力匹配,此时模式串就要从头开始和主串起始的下一个字符匹配了
- 如果使用前缀表,模式串就可以不从头匹配,而是从上次已经匹配的内容开始匹配,找到模式串中第三个字符 b 继续开始与主串第六个字符 b 匹配,因为主串第六个字符 b 之前的 aa 已经在上次匹配成功,主串也不会回退,直接从当前匹配不成功的地方继续比较
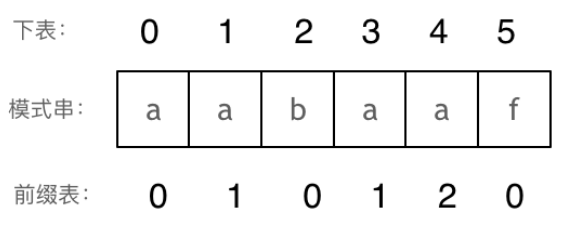
模式串的前缀表元素表示:以当前下标结尾的字符串中,相同前后缀的长度,当模式串与主串不匹配时,模式串直接跳到前一个字符的前缀表的所存下标开始与当前主串字符重新匹配。
KMP 相比于暴力更快的原因:
-
KMP 利用模式串的已匹配部分中相同的「前缀」和「后缀」来加速下一次的匹配
-
KMP 的主串的指针不会回溯
构建 next 数组:双指针。本质是统计模式串的相同前后缀长度
- 初始化慢、快指针分别指向模式串第一个和第二个元素,快指针遍历模式串;
- 当快慢指针指向元素不同且慢指针指向非首时,慢指针循环回退,回退到前一个元素的 next 元素值;
- 当快慢指针指向元素相同时,慢指针向右移动一个单位,最后设置当前快指针位置的 next 数组元素值为慢指针所在位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
func strStr(haystack string, needle string) int {
// 填充next数组
next := make([]int, len(needle))
// 初始前缀末尾指针指向字符串首
i := 0
// 后缀末尾指针从第二个元素开始遍历
for j := 1; j < len(needle); j++ {
// 当俩指针值不同时,不断回退i直至到首或俩指针指向值相同
for i != 0 && needle[i] != needle[j] {
// 前缀指针回退到前一个元素的 next 元素值
i = next[i-1]
}
if needle[i] == needle[j] {
// 俩指针指向值相等时 前缀指针前进一个单位
i++ //
}
// 前缀指针下标赋值给后缀指针指向的next数组
next[j] = i
}
// 在z串中匹配模式串
i = 0 // i指向模式串首
for j := 0; j < len(haystack); j++ { // j指向主串
for i != 0 && haystack[j] != needle[i] { // 主串与模式串字符不相等
i = next[i-1] // 模式串指针回退
}
if haystack[j] == needle[i] { // 主串与模式串字符相等
i++ //模式串前进
}
if i == len(needle) { // 遍历完模式串
return j - len(needle) + 1 // 返回主串中匹配到的模式串首
}
}
return -1
}
|
- 时间复杂度:O(n+m),n为文本串长度,m为模式串长度,匹配过程中文本串的遍历是没有回退过的,所以是O(n),生成next数组需要遍历一遍模式串,所以时间复杂度是O(m),综上整个KMP算法的时间复杂度是O(n+m)的
- 空间复杂度: O(m)
重复的子字符串
459. 重复的子字符串 - 力扣(LeetCode)
给定一个非空的字符串 s ,检查是否可以通过由它的一个子串重复多次构成
思路一暴力:若能被子串构成,则子串是从第一个字符开始的,且子串结束位置不大于中间位置,所以两层for循环,外层遍历获取子串的终止位置,内层遍历判断能否构成主串
注意:要记得判断最后剩余字符数不足以匹配子串的情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
func repeatedSubstringPattern(s string) bool {
// i标记子串末尾,遍历到中间位置
for i := 0; i < len(s)/2; i++ {
// 默认该子串能构成主串
isTrue := true
// j从i+1开始遍历字符串,j每次前进子串长度
for j := i + 1; j < len(s); j += i + 1 {
// 子串与主串不匹配(包括最后剩余字符数不足以匹配)
if len(s)-j < i || s[j:j+i+1] != s[:i+1] {
// 标记该子串无法构成主串
isTrue = false
// 跳出循环,更新子串
break
}
}
if isTrue {
return true
}
}
return false
}
|
思路二:KMP
当 最长相等前后缀不包含的子串的长度 可以被 字符串s的长度整除,那么不包含的子串 就是s的最小重复子串。
next 数组记录的就是最长相同前后缀, 如果 next[len - 1] != -1,则说明字符串有最长相同的前后缀(就是字符串里的前缀子串和后缀子串相同的最长长度)
最长相等前后缀的长度为:next[len - 1]
len - (next[len - 1]) 是最长相等前后缀不包含的子串的长度
如果len % (len - (next[len - 1])) == 0 ,则说明数组的长度正好可以被 最长相等前后缀不包含的子串的长度 整除 ,说明该字符串有重复的子字符串。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
func repeatedSubstringPattern(s string) bool {
// 1.计算next数组
n := len(s)
next := make([]int, n)
i := 0
for j := 1; j < n; j++ {
for i != 0 && s[i] != s[j] {
i = next[i-1]
}
if s[i] == s[j] {
i++
}
next[j] = i
}
// 2.判是否不存在最长相同前后缀
if next[n-1] == 0 {
return false
}
// 3.判最长相等前后缀不包含的子串的长度 能否被 字符串s的长度整除
return n % (n-next[n-1]) == 0
}
|
最后一个单词的长度
58. 最后一个单词的长度 - 力扣(LeetCode)
给定一个字符串,包含空格和连续字符,返回最后一个连续字符的长度
思路:从后向前遍历,找到最后一个字符的位置,向前遍历确定最后一个单词的首字符位置,记录该长度后返回
注意:
- 计数变量需要一开始就初始化,不能在计数循环内初始化,防止最后一单词首字符前再无字符或空格,直接结束循环,无法返回该计数变量
- 找到最后一个字符的位置并计数结束后需要跳出遍历循环,防止字符串继续计数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
func lengthOfLastWord(s string) int {
cnt := 0
// 倒序遍历
for i := len(s) - 1; i >= 0; i-- {
// 找到最后一个字符
if s[i] != ' ' {
// 向前遍历该单词
for j := i; j >= 0; j-- {
if s[j] == ' ' {
return cnt
} else {
cnt++
}
}
// 跳出循环
break
}
}
return cnt
}
|
最长公共前缀
14. 最长公共前缀 - 力扣(LeetCode)
给定一个字符串数组,返回最长公共前缀
思路:
- 初始化第一个字符串为最长公共前缀
- 从第二个字符串遍历给定字符串数组
- 取当前最长公共前缀长度 与 当前字符串长度 的最小值,逐个字符比较当前字符串与当前最长公共前缀
- 每次比较完取min(部分匹配成功, 全部匹配成功)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
func longestCommonPrefix(strs []string) string {
// 初始化第一个字符串为最长公共前缀
res := strs[0]
// 从第二个字符串遍历给定字符串数组
for i := 1; i < len(strs); i++ {
// min(当前最长公共前缀长度, 当前字符串长度)
minlength := min(len(res), len(strs[i]))
// 逐个字符比较当前字符串与当前最长公共前缀
for j := 0; j < minlength; j++ {
// 判对应位置字符是否不同
if strs[i][j] != res[j] {
// 更新最长公共前缀
res = res[:j]
// 结束该字符比较
break
}
}
// res取min(部分匹配成功, 全部匹配成功)
res = res[:min(len(res), minlength)]
}
return res
}
|
Z 字形变换
6. Z 字形变换 - 力扣(LeetCode)
给定一个字符串和一个整数表示行数,将该字符串按上到下、从左到右的Z字形排列,返回从左往右逐行读取的字符串
思路一:利用二维矩阵模拟
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
func convert(s string, numRows int) string {
if numRows == 1 {
return s
}
res := make([][]byte, numRows)
// 标记当前行
curRow := 0
// 标记当前是否为从上往下
isDown := true
// 遍历给定字符串将各字符追加到对应行
for i := 0; i < len(s); i++ {
// 将当前字符追加到对应行
res[curRow] = append(res[curRow], s[i])
// 更新行数
if curRow == numRows-1 {
curRow--
isDown = false
} else if curRow == 0 {
curRow++
isDown = true
} else if isDown {
curRow++
} else {
curRow--
}
}
// 遍历各行
resRow := ""
for _, row := range res {
resRow += string(row)
}
return resRow
}
|
思路二:直接构造
向下填写 numRows 个字符,然后向右上继续填写 numRows−2 个字符,最后回到第一行,因此 Z 字形变换的周期 t = r+r−2 = 2r−2,每个周期会占用矩阵上的 1+r−2 = r−1 列
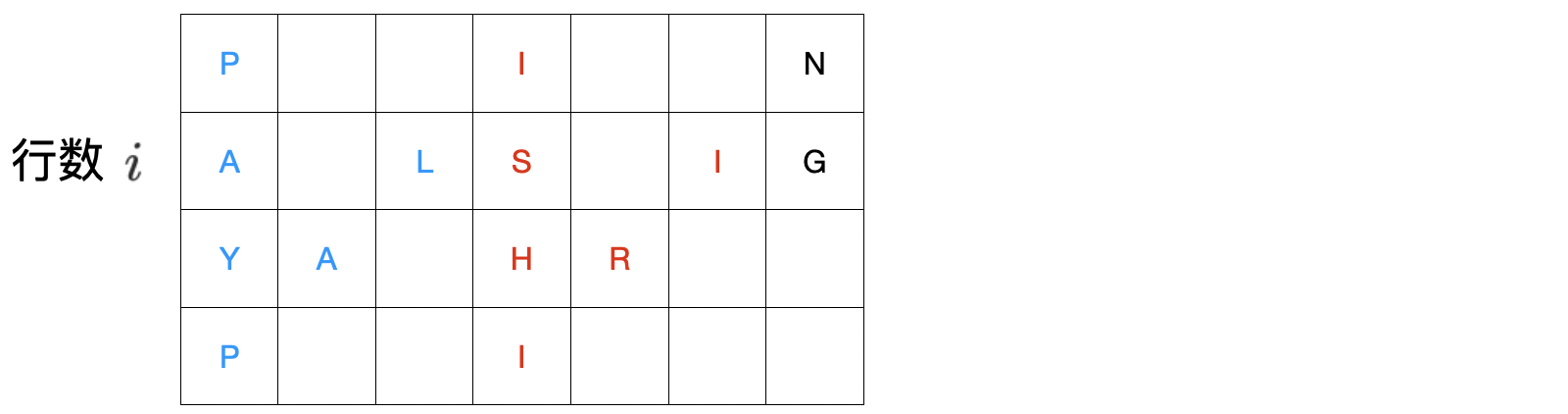
- 记周期长度为
t,t=2(numRows−1)
- 记各周期第一个字符
(P, I, N)在原字符串中的下标为 j,j 依次为 0,t,2t,...
- 那么以图中字符
S 为例,当前行数为 i
- 设顶部字符
I 的下标为 j,实际为 t
- 则
S 的下标为 j+i,与 S 同周期同行的 I 的对应下标为 j+t-i
注意:同一周期内每行可能有两个字符,也可能只有一个
那么可以枚举行数 i,再嵌套枚举 j,得到每行的字符,直接放入待返回的字符串尾部即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
func convert(s string, numRows int) string {
if numRows == 1 {
return s
}
res := make([]byte, 0, len(s))
// 周期长度
t := 2*numRows - 2
// 枚举行数i
for i := 0; i < numRows; i++ {
// 枚举每个周期的起始字符
for j := 0; j+i < len(s); j += t {
// 将当前周期的当前行从左往右的第一个元素追加到结果集
res = append(res, s[j+i])
// 判是否为非首行、末行且未越界元素
if i > 0 && i < numRows-1 && j+t-i < len(s) {
// 将当前周期的当前行的从左往右的第二个元素追加到结果集
res = append(res, s[j+t-i])
}
}
}
return string(res)
}
|
文本左右对齐
68. 文本左右对齐 - 力扣(LeetCode)
给定一个单词数组 words 和一个长度 maxWidth ,重新排版单词,使其成为每行恰好有 maxWidth 个字符,且左右两端对齐的文本。
要求:
- 尽可能多地往每行中放置单词。必要时可用空格
' ' 填充,使得每行恰好有 maxWidth 个字符。
- 要求尽可能均匀分配单词间的空格数量。如果某一行单词间的空格不能均匀分配,则左侧放置的空格数要多于右侧的空格数。
- 文本的最后一行应为左对齐,且单词之间不插入额外的空格
思路:模拟
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
|
func fullJustify(words []string, maxWidth int) []string {
res := make([]string, 0)
tempRow := make([]byte, 0, maxWidth)
spaceIdx := make([]int, 0)
// i遍历给定字符串数组
i := 0
for i < len(words) {
// 判当前行能否放下该单词
if len(tempRow)+len(words[i]) <= maxWidth {
// 加入该单词
tempRow = append(tempRow, []byte(words[i])...)
// 判是否有位置加空格
if len(tempRow) < maxWidth {
tempRow = append(tempRow, ' ')
spaceIdx = append(spaceIdx, len(tempRow)-1)
}
// 判是否为最后一个单词
if i == len(words)-1 {
// 判当前行是否填充完毕
if len(tempRow) < maxWidth {
// 后面直接全部填充空格
n := len(tempRow)
for i := n; i < maxWidth; i++ {
tempRow = append(tempRow, ' ')
}
}
// 收集结果并返回
res = append(res, string(tempRow))
return res
} else {
// 当前单词已处理遍历下一单词
i++
}
} else if len(tempRow) <= maxWidth {
// 判当前行是否填充完
if len(tempRow) == maxWidth {
// 判当前行是否只有一个单词或最后一个字符不为空格
if len(spaceIdx) == 1 || tempRow[len(tempRow)-1] != ' ' {
res = append(res, string(tempRow))
tempRow = make([]byte, 0, maxWidth)
spaceIdx = make([]int, 0)
continue
}
}
// 放不下当前单词 需要补空格
// 判当前行最后一个字符是否为空格且不止这一个空格(非当前行唯一单词)
if len(spaceIdx) != 1 && tempRow[len(tempRow)-1] == ' ' {
// 去除最后一个单词后的空格
tempRow = tempRow[:len(tempRow)-1]
spaceIdx = spaceIdx[:len(spaceIdx)-1]
}
// 计算空位数
cnt := maxWidth - len(tempRow)
// 记录当前遍历到的空格位置
idx := 0
// 从左向右补空格
for cnt != 0 {
// 补一个空格
temp := append(tempRow[:spaceIdx[idx%len(spaceIdx)]], ' ')
tempRow = append(temp, tempRow[spaceIdx[idx%len(spaceIdx)]:]...)
// 更新后续空格位置
for j := idx % len(spaceIdx); j < len(spaceIdx)-1; j++ {
spaceIdx[j+1]++
}
idx++
cnt--
}
}
}
return []string{}
}
|
验证回文串
125. 验证回文串 - 力扣(LeetCode)
给定一个字符串,验证其是否为回文串,要求去除其中的非字母和数字字符,大小写字符视作一样
思路:双指针
- 将所有大写->小写
- 双指针遍历,遇到非字母数字则移动
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
// 写法一:先转化大小写再判断时找有效字符
func isPalindrome(s string) bool {
// 初始化双指针指向首尾
left, right := 0, len(s)-1
// 遍历字符串将所有大写字符转为小写字符
bs := []byte(s)
for i, v := range bs {
if v >= 'A' && v <= 'Z' {
bs[i] = v - 'A' + 'a'
}
}
// 双指针遍历字符串
for left < right {
// 判是否当前俩字符不相等
if bs[left] != bs[right] {
// 判是否有非字母数字字符
if bs[left] < '0' || (bs[left] > '9' && bs[left] < 'a') || bs[left] > 'z' {
left++
} else if bs[right] < '0' || (bs[right] > '9' && bs[right] < 'a') || bs[right] > 'z' {
right--
} else {
// 俩都为字母字符且不相等直接返回false
return false
}
} else {
// 俩字符相等继续比较
left++
right--
}
}
return true
}
// 写法二:先转储有效字符再判断
func isPalindrome(s string) bool {
temp := []byte{}
for _, ch := range s {
if ch >= 'a' && ch <= 'z' {
temp = append(temp, byte(ch))
}
if ch >= 'A' && ch <= 'Z' {
temp = append(temp, byte(ch-'A'+'a'))
}
if ch >= '0' && ch <= '9' {
temp = append(temp, byte(ch))
}
}
left, right := 0, len(temp)-1
for left < right {
if temp[left] != temp[right] {
return false
}
left++
right--
}
return true
}
|
串联所有单词的子串
30. 串联所有单词的子串 - 力扣(LeetCode)
给定一个字符串 s 和一个字符串数组 words。 words 中所有字符串 长度相同。
s 中的 串联子串 是指一个包含 words 中所有字符串以任意顺序排列连接起来的子串。
- 例如,如果
words = ["ab","cd","ef"], 那么 "abcdef", "abefcd","cdabef", "cdefab","efabcd", 和 "efcdab" 都是串联子串。 "acdbef" 不是串联子串,因为他不是任何 words 排列的连接。
返回所有串联子串在 s 中的开始索引。你可以以 任意顺序 返回答案。
思路一:单哈希表
用滑动窗口去匹配
用cnt记录下需要匹配的单词数,如果cnt为0就为全部匹配成功
用哈希表记录每个单词匹配的情况,键为单词,值为需匹配的次数,正数表示还需匹配多少个单词,负数代表已经匹配多了几个单词,为0代表正好匹配完这个单词
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
func findSubstring(s string, words []string) []int {
res := []int{}
wordLen := len(words[0])
// 枚举窗口起始位置wordLen
for start := 0; start < wordLen; start++ {
// 记录还需匹配的各单词数
mp := map[string]int{}
for _, word := range words {
mp[word]++
}
// 记录还需匹配的单词数
cnt := len(words)
left := start
// 开始滑动窗口
// 窗口右边界遍历s, 每次移动一个单词长度
for right := start + wordLen; right <= len(s); right += wordLen {
// 新入窗口的单词
word := s[right-wordLen : right]
// 判该单词是否是需要匹配的
if v, ok := mp[word]; ok {
// 判该单词是否为有效匹配
if v > 0 {
// 更新计数
cnt--
}
// 更新哈希表
mp[word]--
}
// 判当前窗口长度是否为串联子串长度
if right-left == len(words)*wordLen {
// 判还需匹配的单词数是否为0
if cnt == 0 {
res = append(res, left)
}
// 移动左边界(先判是否在哈希表中,若在先更新哈希表)
if v, ok := mp[s[left:left+wordLen]]; ok {
// 判左边界单词是否为有效匹配
if v >= 0 {
// 更新计数
cnt++
}
mp[s[left:left+wordLen]]++
}
left += wordLen
}
}
}
return res
}
|
思路二:双哈希表
题解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
func findSubstring(s string, words []string) []int {
res := []int{} // 结果数组
wordNum := len(words)
if wordNum == 0 {
return res
}
wordLen := len(words[0]) // 每个单词的长度
allWords := make(map[string]int) // 存储所有单词及其出现次数
// 统计 words 中每个单词的出现次数
for _, w := range words {
allWords[w]++
}
// 将所有移动分成 wordLen 类情况
for j := 0; j < wordLen; j++ {
hasWords := make(map[string]int) // 记录当前窗口内单词出现次数
num := 0 // 当前窗口中有效单词的数量
// 每次移动一个单词长度
for i := j; i <= len(s)-wordNum*wordLen; i += wordLen {
hasRemoved := false // 标记是否移除过单词
for num < wordNum {
word := s[i+num*wordLen : i+(num+1)*wordLen] // 当前单词
if _, exists := allWords[word]; exists { // 如果单词在 allWords 中
hasWords[word]++
// 如果出现次数超过预期
if hasWords[word] > allWords[word] {
hasRemoved = true
removeNum := 0
// 一直移除单词,直到次数符合
for hasWords[word] > allWords[word] {
firstWord := s[i+removeNum*wordLen : i+(removeNum+1)*wordLen]
hasWords[firstWord]--
removeNum++
}
num = num - removeNum + 1 // 更新 num
i = i + (removeNum-1)*wordLen // 更新 i
break
}
} else { // 如果遇到不匹配的单词
hasWords = make(map[string]int) // 清空当前窗口
i += num * wordLen // 移动到问题单词后
num = 0
break
}
num++
}
// 如果 num == wordNum,说明找到一个匹配的子串
if num == wordNum {
res = append(res, i)
}
// 移除第一个单词以进行下一次迭代
if num > 0 && !hasRemoved {
firstWord := s[i : i+wordLen]
hasWords[firstWord]--
num--
}
}
}
return res
}
|
字符串的最大公因子
1071. 字符串的最大公因子 - 力扣(LeetCode)
给定两个字符串,求两个字符串的最大公因子
思路:判有解+长度最大公因数
- 判是否存在最大公因子:假设存在最大公因子,则
str1就是m个最大公因子,str2是n个最大公因子。那么str1+str2就是m+n个最大公因子,反过来str2+str1是n+m个最大公因子,两者相等。由此可得,若str1+str2 == str2+str1,则存在最大公因子,反之不存在。
- 求最大公因子:若前面判断出一定存在最大公因子,则最优解一定是
str1和str2长度的最大公因数
1
2
3
4
5
6
7
8
9
10
11
12
|
func gcdOfStrings(str1 string, str2 string) string {
if str1+str2 != str2+str1 {
return ""
}
return str1[:gcd(len(str1), len(str2))]
}
func gcd(a, b int) int {
if b == 0 {
return a
}
return gcd(b, a%b)
}
|
压缩字符串
443. 压缩字符串 - 力扣(LeetCode)
给定一个字符数组 chars ,压缩该字符数组:若该字符只有一个,则不变;若该字符连续且不止一个,则在第一个字符用数字代表后续连续字符长度,若该长度大于等于10,则各个位分开存储为单个字符。最后返回压缩后数组的长度。要求只使用常量额外空间。
思路:快慢指针模拟
快指针遍历字符数组,慢指针标记当前处理到的位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
func compress(chars []byte) int {
slow := 0
for fast := 0; fast < len(chars); fast++ {
cnt := 1
for fast < len(chars)-1 && chars[fast] == chars[fast+1] {
fast++
cnt++
} // 此时fast指向相同字符的最后一个
// 设置该字符
chars[slow] = chars[fast]
slow++
if cnt == 1 {
continue
}
// 设置该字符长度
if cnt <= 9 {
chars[slow] = byte(cnt+'0')
slow++
} else {
strCnt := strconv.Itoa(cnt)
for _, ch := range strCnt {
chars[slow] = byte(ch)
slow++
}
}
}
return slow
}
|
交替合并字符串
1768. 交替合并字符串 - 力扣(LeetCode)
给定两个字符串,交替合并,返回合并后的字符串
思路:双指针交替遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
func mergeAlternately(word1 string, word2 string) string {
idx1, idx2 := 0, 0
res := []byte{}
for idx1 < len(word1) || idx2 < len(word2) {
if idx1 < len(word1) {
res = append(res, word1[idx1])
idx1++
}
if idx2 < len(word2) {
res = append(res, word2[idx2])
idx2++
}
}
return string(res)
}
|
反转字符串中的元音字母
345. 反转字符串中的元音字母 - 力扣(LeetCode)
给定一个字符串 s ,仅反转字符串中的所有元音字母,并返回结果字符串
思路:双指针
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
func reverseVowels(s string) string {
sByte := []byte(s)
idx1, idx2 := 0, len(s)-1
for idx1 < idx2 {
for idx1 < idx2 && idx1 < len(s) && !strings.Contains("aeiouAEIOU", string(s[idx1])) {
idx1++
}
for idx1 < idx2 && idx2 >= 0 && !strings.Contains("aeiouAEIOU", string(s[idx2])) {
idx2--
}
sByte[idx1], sByte[idx2] = sByte[idx2], sByte[idx1]
idx1++
idx2--
}
return string(sByte)
}
|
LCR 122. 路径加密
LCR 122. 路径加密 - 力扣(LeetCode)
假定一段路径记作字符串 path,其中以 “.” 作为分隔符。现需将路径加密,加密方法为将 path 中的分隔符替换为空格 “ ",请返回加密后的字符串。
剑指offer中是将每个空格替换为%20
1
2
3
4
5
6
7
8
9
|
func pathEncryption(path string) string {
pathByte := []byte(path)
for i, ch := range pathByte {
if ch == '.' {
pathByte[i] = ' '
}
}
return string(pathByte)
}
|
字符串转换整数 (atoi)
8. 字符串转换整数 (atoi) - 力扣(LeetCode)
给定一个字符串,包含空格、正负号、数字字符、小数点,且出现顺序一定是空格、正负号、数字字符。若数字超过32位或小于32位整数,则需要截断或舍入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
func myAtoi(s string) int {
// 1.去掉前导空格
i := 0
for i < len(s) && s[i] == ' ' {
i++
}
// 2.读取符号
// 默认为正
sign := 1
if i < len(s) {
if s[i] == '-' {
sign = -1
i++
} else if s[i] == '+' {
sign = 1
i++
}
}
// 3.读取数字字符串
res := 0
for i < len(s) && s[i] >= '0' && s[i] <= '9' {
res = 10*res + int(s[i]-'0')
// 判是否越界
if sign*res < math.MinInt32 {
return math.MinInt32
} else if sign*res > math.MaxInt32 {
return math.MaxInt32
}
i++
}
return sign * res
}
|
有效数字
65. 有效数字 - 力扣(LeetCode)
给定一个字符串 s ,返回 s 是否是一个 有效数字。
例如,下面的都是有效数字:"2", "0089", "-0.1", "+3.14", "4.", "-.9", "2e10", "-90E3", "3e+7", "+6e-1", "53.5e93", "-123.456e789",而接下来的不是:"abc", "1a", "1e", "e3", "99e2.5", "--6", "-+3", "95a54e53"。
有效数字:
- 整数 + 可选指数:可选符号 + 数字 + 可选指数(
e/E + 符号 + 数字)
- 十进制数 + 可选指数:
- 可选符号 + 数字 +
. + 可选指数
- 可选符号 + 数字 +
. + 数位 + 可选指数
- 可选符号 +
. + 数位 + 可选指数
定义
- 整数 :
'-/+' + 数字
- 指数 :
e/E + 整数
- 数字:一个或多个数位
- 数位:单个数字
思路:有限状态自动机
力扣官方题解
- 起初,自动机处于「初始状态」
- 随后,它顺序地读取字符串中的每一个字符,并根据当前状态和读入的字符,按照某个事先约定好的「转移规则」,从当前状态转移到下一个状态
- 当状态转移完成后,它就读取下一个字符
- 当字符串全部读取完毕后,如果自动机处于某个「接受状态」,则判定该字符串「被接受」;否则,判定该字符串「被拒绝」
- 输入的过程中某一步转移失败了,即不存在对应的「转移规则」,此时计算将提前中止。在这种情况下判定该字符串「被拒绝」
自动机驱动的编程,可以被看做一种暴力枚举方法的延伸:它穷尽了在任何一种情况下,对应任何的输入,需要做的事情。
自动机在计算机科学领域有着广泛的应用。在算法领域,它与字符串查找算法「KMP 算法」有着密切的关联;在工程领域,它是实现「正则表达式」的基础
在 C++ 文档 中,描述了一个合法的数值字符串应当具有的格式。具体而言,它包含以下部分:
在上面描述的五个部分中,每个部分都不是必需的,但也受一些额外规则的制约,如:
- 如果符号位存在,其后面必须跟着数字或小数点。
- 小数点的前后两侧,至少有一侧是数字。
定义自动机的「状态集合」:用「当前处理到字符串的哪个部分」当作状态的表述。挖掘出所有状态:
找出「初始状态」和「接受状态」的集合:根据题意,「初始状态」为状态 0,而「接受状态」的集合则为状态 2、状态 3、状态 5 以及状态 8。换言之,字符串的末尾要么是空格,要么是数字,要么是小数点,但前提是小数点的前面有数字。
最后,需要定义「转移规则」。结合数值字符串应当具备的格式,将自动机转移的过程以图解的方式表示出来:
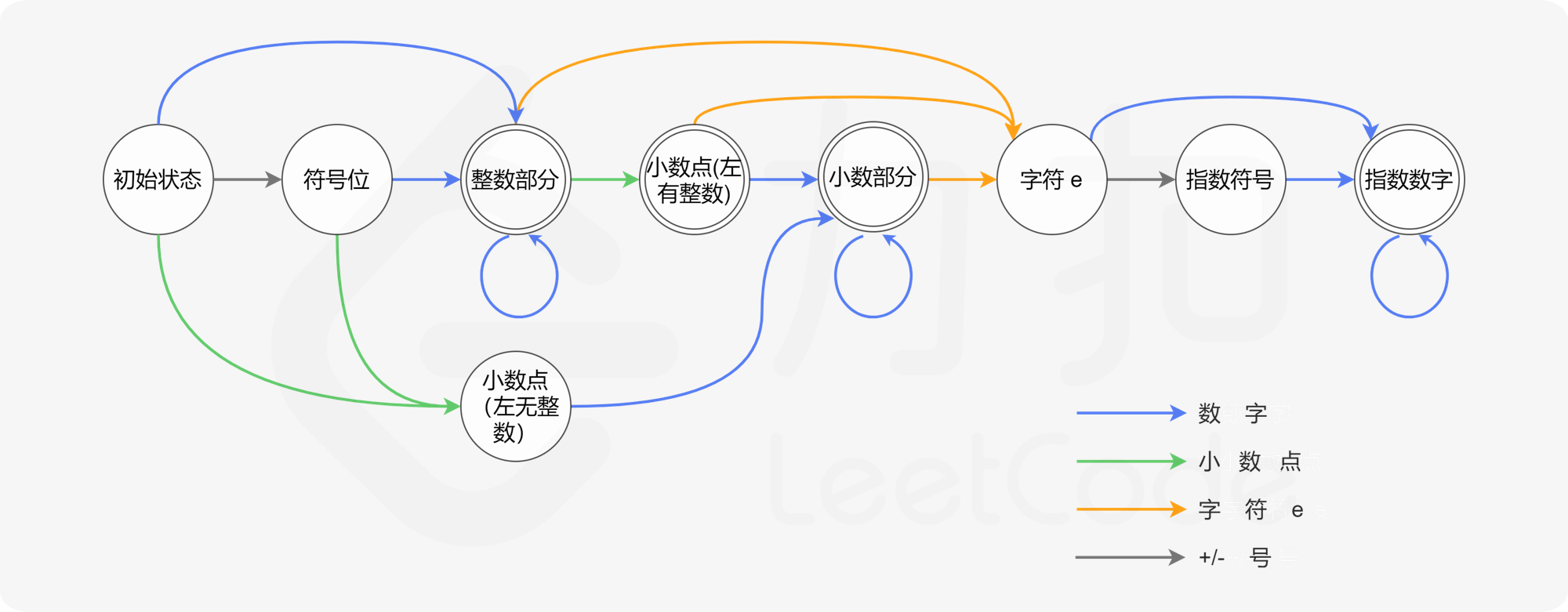
没有单独地考虑每种字符,而是划分为若干类。由于全部 10 个数字字符彼此之间都等价,因此只需定义一种统一的「数字」类型即可。对于正负号也是同理。
在实际代码中,需要处理转移失败的情况。为了处理这种情况,可以创建一个特殊的拒绝状态。如果当前状态下没有对应读入字符的「转移规则」,就转移到这个特殊的拒绝状态。一旦自动机转移到这个特殊状态,就可以立即判定该字符串不「被接受」
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
|
type State int
type CharType int
// 定义10个状态(0~9)
const (
STATE_INITIAL State = iota // 初始状态
STATE_INT_SIGN // 符号位
STATE_INTEGER // 整数部分
STATE_POINT // 左侧有整数的小数点
STATE_POINT_WITHOUT_INT // 左侧无整数的小数点
STATE_FRACTION // 小数部分
STATE_EXP // 字符 e
STATE_EXP_SIGN // 指数部分的符号位
STATE_EXP_NUMBER // 指数部分的整数部分
STATE_END // 拒绝状态
)
// 定义五种字符类型
const (
CHAR_NUMBER CharType = iota // 数字
CHAR_EXP // 字符 e 或 E
CHAR_POINT // 小数点
CHAR_SIGN // 符号
CHAR_ILLEGAL // 非法字符
)
// 将一个字符转换为对应的字符类型
func toCharType(ch byte) CharType {
switch ch {
case '0', '1', '2', '3', '4', '5', '6', '7', '8', '9':
return CHAR_NUMBER
case 'e', 'E':
return CHAR_EXP
case '.':
return CHAR_POINT
case '+', '-':
return CHAR_SIGN
default:
return CHAR_ILLEGAL
}
}
func isNumber(s string) bool {
// key: 状态 v: 该状态在遇到对应字符后可转换到的下一状态
transfer := map[State]map[CharType]State{
STATE_INITIAL: map[CharType]State{
CHAR_NUMBER: STATE_INTEGER,
CHAR_POINT: STATE_POINT_WITHOUT_INT,
CHAR_SIGN: STATE_INT_SIGN,
},
STATE_INT_SIGN: map[CharType]State{
CHAR_NUMBER: STATE_INTEGER,
CHAR_POINT: STATE_POINT_WITHOUT_INT,
},
STATE_INTEGER: map[CharType]State{
CHAR_NUMBER: STATE_INTEGER,
CHAR_EXP: STATE_EXP,
CHAR_POINT: STATE_POINT,
},
STATE_POINT: map[CharType]State{
CHAR_NUMBER: STATE_FRACTION,
CHAR_EXP: STATE_EXP,
},
STATE_POINT_WITHOUT_INT: map[CharType]State{
CHAR_NUMBER: STATE_FRACTION,
},
STATE_FRACTION: map[CharType]State{
CHAR_NUMBER: STATE_FRACTION,
CHAR_EXP: STATE_EXP,
},
STATE_EXP: map[CharType]State{
CHAR_NUMBER: STATE_EXP_NUMBER,
CHAR_SIGN: STATE_EXP_SIGN,
},
STATE_EXP_SIGN: map[CharType]State{
CHAR_NUMBER: STATE_EXP_NUMBER,
},
STATE_EXP_NUMBER: map[CharType]State{
CHAR_NUMBER: STATE_EXP_NUMBER,
},
}
// 当前状态初始化为初始状态
state := STATE_INITIAL
// 遍历字符
for i := 0; i < len(s); i++ {
// 将一个字符转换为对应的字符类型,用整数表示
typ := toCharType(s[i])
// 判当前状态遇到该字符能否成功转换到下一状态
if _, ok := transfer[state][typ]; !ok {
return false
} else {
// 根据输入字符更新当前状态
state = transfer[state][typ]
}
}
// 最后判断是否达到一个合法的状态
return state == STATE_INTEGER || state == STATE_POINT || state == STATE_FRACTION || state == STATE_EXP_NUMBER || state == STATE_END
}
|
字符流中第一个不重复的字符⚫
JZ75 字符流中第一个不重复的字符_牛客题霸_牛客网
给定一个字符串,逐个读取字符,找出读取到当前位置为止第一个只出现一次的字符,没有则为#,返回找到的各字符组成的字符串
思路:队列+哈希表
- 用队列记录输入的字符流,用哈希表统计每个字符的出现次数,二者都是全局变量。
- 输入的字符加到队列最后,然后统计出现次数
- 不断检查队首元素直到队列为空或队首出现次数为1次,队首出现次数不为1就弹出
- 最后,若队空,则返回
#,否则返回队首
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
package main
// 队列保存顺序读取的所有字符
var queue []int
// mp 记录各字符的出现次数
var mp [128]int
// 获取一个字符
func Insert(ch byte) {
// 字符入队
queue = append(queue, int(ch))
// 更新次数
mp[int(ch)]++
}
// 返回当前第一个只出现一次的字符
func FirstAppearingOnce() byte {
// 不断检查直至队空或队首字符出现次数为1
for len(queue) != 0 && mp[int(queue[0])] != 1 {
queue = queue[1:]
}
if len(queue) == 0 {
return '#'
}
return byte(queue[0])
}
func init() {
queue = []int{}
mp = [128]int{}
}
|


