理论基础
数组是非常基础的数据结构,在面试中,考察数组的题目一般在思维上都不难,主要是考察对代码的掌控能力。也就是说,想法很简单,但实现起来可能就不是那么回事了
首先要知道数组在内存中的存储方式,这样才能真正理解数组相关的面试题,数组是存放在连续内存空间上的相同类型数据的集合
数组可以方便的通过下标索引的方式获取到下标所对应的数据,需要两点注意的是
- 数组下标都是从0开始的。
- 数组内存空间的地址是连续的
正是因为数组的在内存空间的地址是连续的,所以在删除或者增添元素的时候,就难免要移动其他元素的地址
二分查找
704. 二分查找 - 力扣(LeetCode)
给定一个升序的整数数组和一个目标值,返回数组中目标值的下标,若没有返回-1
思路一:遍历数组
1
2
3
4
5
6
7
8
|
func search(nums []int, target int) int {
for i, v := range nums {
if v == target {
return i
}
}
return -1
}
|
思路二:二分查找,定义初始区间索引为给定数组索引;比较区间的中间值和目标值的大小,若区间中间值小于目标值,说明目标值在区间中间值右半部分,调整区间左索引为中间索引+1;若区间中间值大于目标值,说明目标值在区间中间值左半部分,调整区间右索引为中间索引-1;若区间中间值等于目标值,返回中间值索引
注意:
- 调整区间索引时要设为中间索引的前一个或后一个
- 使用二分查找的数组要是有序的
- 求中间索引时为了防止求和后整数溢出,可以用left+(right-left)/2,即先求出区间元素个数的一半,再从左边界前进该个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
func search(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right { // 当left = right时[left, right]依然有效
mid := left + (right - left) / 2 // 获得区间中间索引
if nums[midIdx] == target {
return midIdx // 找到目标值
} else if nums[midIdx] < target {
left = midIdx + 1 // 目标值在右区间
} else { // nums[midIdx] > target
right = midIdx - 1 // 目标值在左区间
}
}
return -1
}
|
搜索插入位置
35. 搜索插入位置 - 力扣(LeetCode)
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引,如果目标值不存在于数组中,返回它将会被按顺序插入的位置,必须使用时间复杂度为 O(log n) 的算法
只要看到面试题里给出的数组是有序数组,都可以想一想是否可以使用二分法,同时题目还强调数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的
二分查找若直到左区间大于右区间仍未找到目标值,则看最后左区间等于右区间时的元素值,若最后的中间值大于目标值,则返回该中间值下标,否则返回该中间值下一元素下标
简化:若二分查找结束没找到目标值,直接返回区间右边界加一或左边界;因为若最后的中间值小于目标值,说明目标值在右半区间,目标值要插入到最后中间值的后面一个,而此时只调整了左边界,右边界没动,还指向最后的中间值;若最后的中间值大于目标值,说明目标值在左半区间,目标值要插入到最后的中间值位置,此时右边界被移到最后中间值的前一个元素,右边界再加一刚好是最后的中间值位置;若最后的中间值等于目标值,则插入到最后的中间值位置或后面一个都可以
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
func searchInsert(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right - left) / 2
if nums[mid] == target {
return mid
} else if nums[mid] < target {
left = mid + 1 // 目标值在右半区间
} else {
right = mid - 1 // 目标值在左半区间
}
}
return right + 1 // 返回插入位置
// return left
}
|
- 时间复杂度:O(log n)
- 空间复杂度:O(1)
暴力解法
1
2
3
4
5
6
7
8
9
10
11
12
|
func searchInsert(nums []int, target int) int {
// 遍历数组
for i, v := range nums {
// 判断元素是否大于或等于目标值
if v >= target {
// 直接返回当前索引
return i
}
}
// 目标值最大
return len(nums)
}
|
在排序数组中查找元素的第一个和最后一个位置
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
给定一个递增数组和目标值 ,找出给定目标值在数组中的开始位置和结束位置,如果数组中不存在目标值,返回 [-1, -1],必须设计并实现时间复杂度为 O(log n) 的算法解决此问题
思路一:数组中含有重复元素,用二分查找到目标元素后,再向两边继续查找相同元素并记录下标,直到遇到不同元素,返回目标值的区间
注意:
- 找到目标区间后直接跳出循环返回结果
- 结果区间要初始化为0,避免当给定数组中只有一个元素且刚好是目标值时,向两边找不到不同元素,最后直接返回结果区间的初始值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
func searchRange(nums []int, target int) []int {
left, right := 0, len(nums)-1
resLeft, resRight := 0, 0
for left <= right {
mid := left + (right - left) / 2
if nums[mid] == target {
for i := mid; i < len(nums); i++ { // 从目标值向右遍历
if nums[i] != target {
break
}
resRight = i // 更新右边界
}
for i := mid; i >= 0; i-- { // 从目标值向左遍历
if nums[i] != target {
break
}
resLeft = i // 更新左边界
}
return []int{resLeft, resRight}
} else if nums[mid] > target {
right = mid - 1 // 目标值在左区间
} else {
left = mid + 1 // 目标值在右区间
}
}
return []int{-1, -1}
}
|
思路二:分别用两个二分查找左右边界;在找左边界的二分查找中找到目标值后需要判断目标值的上一个元素是否与目标值不同,若不同或已经是数组的第一个元素则说明此中间值是左边界,否则继续更新右边界向左半区间查找;同理,在找右边界的二分查找中找到目标值后需要判断目标值的下一个元素是否与目标值不同,若不同或已经是数组最后一个元素则说明此中间值是右边界,否则继续更新左边界向右半区间查找
注意:在遇到目标值后,若判断不是边界,则需要更新二分查找边界
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
func searchRange(nums []int, target int) []int {
left := searchLeft(nums, target)
right := searchRight(nums, target)
return []int{left, right}
}
func searchLeft(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right-left)/2
if nums[mid] == target { // 找到目标值
if mid == 0 || nums[mid-1] != target {
return mid
} else { // 不是第一个目标值
right = mid - 1 // 向左搜索更新右边界
}
} else if nums[mid] < target {
left = mid + 1
} else {
right = mid - 1
}
}
return -1 // 没找到左边界
}
func searchRight(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right-left)/2
if nums[mid] == target { // 找到目标值
if mid == len(nums)-1 || nums[mid+1] != target {
return mid
} else { // 不是最后一个目标值
left = mid + 1 // 向右搜索更新左边界
}
} else if nums[mid] > target {
right = mid - 1
} else {
left = mid + 1
}
}
return -1 // 没找到右边界
}
|
- 时间复杂度:O(log n)
- 空间复杂度:O(1)
x 的平方根
69. x 的平方根 - 力扣(LeetCode)
给你一个非负整数 ,返回算术平方根,结果只保留整数部分,舍去小数部分
一个数x的算术平方根一定在0~x/2,升序数组,考虑使用二分查找法找到目标元素
在二分查找过程中有三种情况
- 如果这个整数的平方等于输入整数,那么我们就找到了这个整数;
- 如果这个整数的平方大于输入整数,那么这个整数肯定不是我们要找的那个数;
- 如果这个整数的平方小于输入整数,那么这个整数可能是我们要找的那个数 (算术平方根为小数时只保留整数)。
若算术平方根是小数,则最后一轮循环中,mid是第一个大于x/mid的值,所以在左区间寻找,执行right = mid -1 ,此时right < left,结束循环,right就是只保留整数的算术平方根
注意:
- 若直接使用
mid*mid == x判断,乘数可能会发生整数溢出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
func mySqrt(x int) int {
left, right := 0, x
if x <= 1 {
return x
}
for left <= right {
mid := left + (right-left)/2
if mid == x/mid {
return mid
} else if mid < x/mid {
left = mid + 1
} else {
right = mid - 1
}
}
return right
}
|
- 时间复杂度:O(log n)
- 空间复杂度:O(1)
有效的完全平方数
367. 有效的完全平方数 - 力扣(LeetCode)
给给定一个正整数 。若是一个完全平方数,则返回 true ,否则返回 false ,例如16是完全平方数,因为4*4=16,14不是完全平方数,因为3.742 * 3.742 = 14,但 3.742 不是一个整数
用二分法查找给定整数的平方根,若能找到返回true,否则返回false
注意:
-
判断条件不能写mid == num/mid,只能写mid * mid == num,因为num/mid为int类型,会导致结果错误
例如:当num=5, mid=2时,mid == num/mid为true,而num并不是完全平方数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
func isPerfectSquare(num int) bool {
left, right := 1, num/2
if num <= 1 {
return true
}
for left <= right {
mid := left + (right-left)/2
if mid*mid == num {
return true
} else if mid*mid < num {
left = mid + 1
} else {
right = mid - 1
}
}
return false
}
|
- 时间复杂度:O(log n)
- 空间复杂度:O(1)
移除元素
27. 移除元素 - 力扣(LeetCode)
给定一个数组和目标值,原地移除数组中等于目标值的元素,返回移除后数组的长度,要求不能使用额外的数组空间
思路一:暴力,外层循环遍历数组,每遇到一个目标值就在内层循环中将后面的所有元素前移一个单位;前移结束后设置下一次遍历位置为仍为当前下标,数组长度减一;若当前元素不是目标值,则下一次遍历位置为下一元素
注意:遍历结束的标志是移除后数组的长度
1
2
3
4
5
6
7
8
9
10
11
12
13
|
func removeElement(nums []int, val int) int {
size := len(nums)
for i := 0; i < size; i++ {
if nums[i] == val {
for j := i; j < len(nums)-1; j++ {
nums[j] = nums[j+1] // 元素前移一个单位
}
i-- // 下次循环仍从当前元素位置开始
size-- // 数组长度减一
}
}
return size
}
|
思路二:双指针(快慢指针),在一个循环中完成两个循环的工作;快指针寻找与目标值不同的新元素,慢指针指向要更新的下标;将快指针指向的新元素更新到前面慢指针指向的元素;当快指针遍历结束后,返回最后慢指针指向的下标即可
快慢指针都从头出发;快指针遍历数组,当快指针指向的元素与目标值不同时,将快指针指向的元素值赋给慢指针指向的元素,然后慢指针前进一步(快指针遇到与目标值不同的元素时,快慢指针同步前进);当快指针指向的元素与目标值相同时,慢指针不动此时指向要更新的元素,快指针继续前进,快指针遇到的元素若仍与目标值相同,慢指针仍不动,快指针继续前进,直到快指针遇到与目标值不同的元素,此时快指针的指向的元素会赋给此时慢指针指向的要更新的元素,更新后慢指针前进一个单位指向下一个要更新元素
1
2
3
4
5
6
7
8
9
10
|
func removeElement(nums []int, val int) int {
slowIdx := 0
for fastIdx := 0; fastIdx < len(nums); fastIdx++ {
if nums[fastIdx] != val {
nums[slowIdx] = nums[fastIdx] // 更新元素
slowIdx++ // 慢指针前进一步
}
}
return slowIdx
}
|
删除有序数组中的重复项
26. 删除有序数组中的重复项 - 力扣(LeetCode)
给定一个递增数组,原地移除数组中重复的元素,使每个元素只出现一次,返回移除后数组的长度,要求不能使用额外的数组空间
双指针法:快指针遍历数组寻找新元素,慢指针指向要更新的元素下标,将快指针指向的元素更新到慢指针指向的元素,快指针遍历结束后,返回慢指针指向的下标
初始时将第一个元素置为目标值,快慢指针遍历从第二个元素开始,当快指针遇到新元素,更新目标值为新元素,更新慢指针指向元素的值,慢指针前进
简化:省去目标值变量,判断快指针是否遇到新元素,直接与快指针指向的前一个元素比较
1
2
3
4
5
6
7
8
9
10
|
func removeDuplicates(nums []int) int {
slowIdx := 1
for fastIdx := 1; fastIdx < len(nums); fastIdx++ {
if nums[fastIdx] != nums[fastIdx-1] { // 找到新元素
nums[slowIdx] = nums[fastIdx] // 更新慢指针指向元素
slowIdx++ // 慢指针前进
}
}
return slowIdx
}
|
移动零
283. 移动零 - 力扣(LeetCode)
给定一个数组,将数组中所有的0都移到末尾,要求其余元素顺序不变,必须在不复制数组的情况下原地对数组进行操作
暴力:遍历数组,每遇到一个0就将所有元素前移一个,同时将末尾元素置为0,时间复杂度O(n2)
双指针法:类似用快慢指针移除元素的操作,目标值为0,快指针遍历数组,慢指针标记要更新的元素,当快指针遇到非目标值说明要更新慢指针指向的目标值
由于是将0移到数组末尾,并非是完全移除,所有当快指针找到不为0的数时,将慢指针和快指针的值交换即可,这样会将非0值逐个换到前面的0所在位置
进一步理解:慢指针标记当前处理到的地方
1
2
3
4
5
6
7
8
9
|
func moveZeroes(nums []int) {
slowIndex := 0
for fastIndex := 0; fastIndex < len(nums); fastIndex++ {
if nums[fastIndex] != 0 {
nums[slowIndex], nums[fastIndex] = nums[fastIndex], nums[slowIndex] // 更新慢指针指向元素
slowIndex++ // 慢指针前进
}
}
}
|
比较含退格的字符串
844. 比较含退格的字符串 - 力扣(LeetCode)
给定两个字符串,# 代表退格字符,若两者相等返回 true ,否则返回false,如果对空文本输入退格字符,文本仍为空
思路一:快慢指针
对两个字符串分别使用快慢指针,得到退格后的有效字符串,最后直接用==判断:快指针遍历字符串,当快指针遇到有效字符时,则将快指针指向值赋给慢指针指向值(表示退格符后有效元素前移替换了删除的元素),最后慢指针前进一个单位;当快指针遇到退格符且慢指针指向非首时,则慢指针回退一个(指向要删除的元素);
注意:由于字符串不可修改,所以需要将字符串不可变性
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
func backspaceCompare(s string, t string) bool {
// 判断俩有效字符串是否相等
return getString(s) == getString(t)
}
func getString(s string) string {
slow := 0
// 将字符串转换为字符数组
byteArray := []byte(s)
// 快指针遍历字符数组
for fast := range byteArray {
// 判断是否遇到有效字符
if byteArray[fast] != '#' {
// 更新慢指针值(替换元素)
byteArray[slow] = byteArray[fast]
// 慢指针后移
slow++
} else if slow != 0 {
// 慢指针前移(指向删除元素)
slow--
}
}
// 返回有效字符串
return string(byteArray[:slow])
}
|
- 时间复杂度:O(n+m)
- 空间复杂度:O(n+m)
思路二:栈
匹配(消除)问题也是栈的擅长所在:两个字符串分别用两个栈,遇到退格符,栈顶弹出,遇到有效字符,入栈,最后比较两个栈里元素是否相等
注意:
for range遍历字符串时,每个字符是rune类型- 每次遇到弹栈,都要先判栈非空
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
func backspaceCompare(s string, t string) bool {
return getSting(s) == getSting(t)
}
func getSting(s string) string {
stack := make([]rune, 0)
// 遍历字符串s
for _, ch := range s {
// 判断是否为有效字符
if ch != '#' {
// 入栈
stack = append(stack, ch)
} else if len(stack) != 0 {
// 弹栈
stack = stack[:len(stack)-1]
}
}
return string(stack)
}
|
- 时间复杂度:O(n + m)
- 空间复杂度:O(n + m)
思路三:模拟退格
由于 # 号只会消除左边的一个字符,所以对右边的字符无影响,所以选择从后往前遍历 S,T 字符串。
思路解析:
- 准备两个指针分别指向俩字符串的末位字符,再准备两个变量 skipS,skipT存俩字符串中的 # 数量
- 从后往前遍历 S,所遇情况有三,如下所示:
- 若当前字符是 #,则 skipS 自增 1;
- 若当前字符不是 #,且 skipS 不为 0,则 skipS 自减 1;
- 若当前字符不是 #,且 skipS 为 0,则代表当前字符不会被消除,我们可以用来和 T 中的当前字符作比较。
若对比过程出现 S, T 当前字符不匹配,则遍历结束,返回 false,若 S,T 都遍历结束,且都能一一匹配,则返回 true。
一个字符是否会被删掉,只取决于该字符后面的退格符,而与该字符前面的退格符无关。因此逆序地遍历字符串,就可以立即确定当前字符是否会被删掉。
具体地,我们定义 skip 表示当前待删除的字符的数量。每次我们遍历到一个字符:
这样,我们定义两个指针,分别指向两字符串的末尾。每次我们让两指针逆序地遍历两字符串,直到两字符串能够各自确定一个字符,然后将这两个字符进行比较。重复这一过程直到找到的两个字符不相等,或遍历完字符串为止
注意:
具体代码可以去看力扣官方题解
有序数组的平方
977. 有序数组的平方 - 力扣(LeetCode)
给定一个非递减的整数数组,要求返回每个数字的平方组成的新数组,新数组也要非递减
考虑到原数组中有负数,原数组元素逐个直接平方后可能会出现递减数组
思路一:暴力,逐个元素平方,然后对元素排序
1
2
3
4
5
6
7
|
func sortedSquares(nums []int) []int {
for i := range nums {
nums[i] = nums[i] * nums[i]
}
sort.Ints(nums)
return nums
}
|
- 时间复杂度:O(n + nlogn) = O(nlogn);但为了和下面双指针法算法时间复杂度有鲜明对比,记为 O(n + nlogn)
思路二:双指针,省去排序操作;两个指针分别指向给定数组的首尾,由于给定数组是递增的,所以平方后的大值一定在两端;开辟一个结果数组,每次比较首尾两个指针指向元素平方后的值,大值存入结果数组的末尾,大值指针移动,小值指针不变等待下次比较,重复上述步骤直到俩指针错位,返回结果数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
func sortedSquares(nums []int) []int {
leftIdx, rightIdx := 0, len(nums)-1
res := make([]int, len(nums))
resIdx := len(res) - 1
for leftIdx <= rightIdx {
if nums[leftIdx]*nums[leftIdx] > nums[rightIdx]*nums[rightIdx] {
res[resIdx] = nums[leftIdx] * nums[leftIdx]
leftIdx++ // 左指针移动一个单位
} else {
res[resIdx] = nums[rightIdx] * nums[rightIdx]
rightIdx-- // 右指针移动一个单位
}
resIdx-- // 结果集指针移动一个单位
}
return res
}
|
长度最小的子数组
209. 长度最小的子数组 - 力扣(LeetCode)
给定一个整数数组和一个目标值 ,找出数组中一个连续子数组,要求其总和要大于等于目标值,且长度要最小,若能找到则返回长度,若找不到返回0
暴力:一个for循环定滑动窗口的起始位置,一个for循环定滑动窗口的终止位置,用两个for循环完成一个不断搜索区间的过程,会超时
双指针(滑动窗口):用一个for循环和一个内层while循环来不断调节子数组的起始位置和终止位置,从而得出结果;for循环控制子数组终止位置;while循环控制起始位置;若当前窗口值大于等于目标值,则统计长度,起始位置后移一个单位,直到当前窗口值小于目标值退出while循环,进入下一次for循环,终止位置更新,重复上述步骤,直至终止位置到给定数组末尾
注意:结果初始化为给定数组长度加一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
func minSubArrayLen(target int, nums []int) int {
left := 0
sum := 0
res := len(nums) + 1
for right := range nums {
sum += nums[right]
for sum >= target {
length := right - left + 1 // 子数组长度
if length < res {
res = length
}
sum -= nums[left] // 更新子数组和
left++ // 更新起始位置
}
}
if res == len(nums)+1 {
return 0 // 没有符合条件的子数组
}
return res
}
|
不要以为for里放一个while就以为是O(n2),时间复杂度主要是看每一个元素被操作的次数,每个元素在滑动窗口进来操作一次,出去操作一次,每个元素都是被操作两次,所以时间复杂度是 2 × n 也就是O(n)
水果成篮
904. 水果成篮 - 力扣(LeetCode)
给定一个数组,找至多包含两种元素的最长子串,返回其长度
最小滑窗模板:给定数组 nums,定义滑窗的左右边界 i, j,求满足某个条件的滑窗的最小长度。
1
2
3
4
5
6
|
while j < len(nums):
判断[i, j]是否满足条件
while 满足条件:
不断更新结果(注意在while内更新!)
i += 1 (最大程度的压缩左边界,使得滑窗尽可能的小)
j += 1
|
最大滑窗模板:给定数组 nums,定义滑窗的左右边界 i, j,求满足某个条件的滑窗的最大长度。
1
2
3
4
5
6
|
while j < len(nums):
判断[i, j]是否满足条件
while 不满足条件:
i += 1 (最保守的压缩左边界,一旦满足条件了就退出压缩左边界的过程,使得滑窗尽可能的大)
不断更新结果(注意在while外更新!)
j += 1
|
最小滑窗是在迭代右移左边界的过程中更新结果,而最大滑窗是在迭代右移右边界的过程中更新结果。
判断滑动窗口内是否满足题设条件有两种选择:
- 遍历这个滑窗来判断是否满足需要,总时间会退化为O(N2)
- 选择字典,用空间换时间,总时间为O(N).
用哈希表存储窗口内的数以及出现的次数,若出现的数多于两个,则说明不满足条件;每次将 right 移动一个位置,并将 fruits[right] 加入哈希表。如果此时哈希表不满足要求(即哈希表中出现超过两个键值对),那么需要不断移动 left,并将 fruits[left] 在哈希表中的值减一,当值减少到 0 时,需要将对应的键值对从哈希表中移除,直到哈希表满足要求为止
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
func totalFruit(fruits []int) int {
left := 0
res := 0
countMap := make(map[int]int)
for right := range fruits {
countMap[fruits[right]]++
for len(countMap) > 2 { // 不满足条件
countMap[fruits[left]]-- // 更新哈希表
if countMap[fruits[left]] == 0 {
delete(countMap, fruits[left]) // 删除出现次数为0的元素
}
left++ // 左边界后移
}
res = max(res, right-left+1) // 更新窗口最大长度
}
return res
}
|
最小覆盖子串
76. 最小覆盖子串 - 力扣(LeetCode)
给定两个字符串,返回第一个字符串中涵盖第二个字符串中所有字符的最小子串,重复字符也必须在子串中出现至少同样次数,如果不存在则返回空字符串
维护一个滑动窗口:右边界不断移动,直到在s中找到覆盖t所有字符的子串,记入结果,不断调整左边界,若仍覆盖,则更新结果,若不覆盖了就调整右边界,直到覆盖了,再更新结果,不断调整左边界,直到右边界遍历结束
用哈希表存储第二个字符串的字符以及出现的次数,其值也表示字符串t中对应字符未出现在子串中的次数;用一个变量统计子串中应出现的字符个数;若查询哈希表得知对应字符出现在哈希表,则在更新哈希表之前检查哈希值是否大于0,若大于0,则说明该字符是有效字符,更新统计子串中应出现的字符个数的变量;若子串中应出现的字符个数为0,则说明满足条件
注意:由于子串中某字符数量可能大于目标串中该字符数量但其他字符没有被覆盖到,所以某字符字典值可能为负值,但count计数大于0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
func minWindow(s string, t string) string {
res := ""
// 记录t中各字符的次数
mp := make(map[byte]int)
// 记录还没有覆盖到的字符个数
count := len(t)
// 滑动窗口左边界
left := 0
// 遍历t计入字典
for i := 0; i < len(t); i++ {
mp[t[i]]++
}
// 滑动窗口右边界right遍历s
for right := range s {
// 判断字典中是否有该字符
if _, ok := mp[s[right]]; ok {
// 判断该字符是否还需要覆盖
if mp[s[right]] > 0 {
// 更新计数
count--
}
// 更新字典值
mp[s[right]]--
}
// 已全部覆盖
for count == 0 {
// 判断结果集是否为空或当前窗口长度小于结果集
if len(res) == 0 || right-left+1 < len(res) {
// 更新结果
res = s[left : right+1]
}
// 判断左边界字符是否在字典中
if _, ok := mp[s[left]]; ok {
// 判断该字符是否恰好被覆盖
if mp[s[left]] == 0 {
// 更新计数
count++
}
// 更新字典值
mp[s[left]]++
}
// 更新左边界
left++
}
}
return res
}
|
- 时间复杂度:$O(n)$,虽然有嵌套循环,但每个字符最多被操作两次,所以整体上仍然是线性的时间复杂度
- 空间复杂度:$O(m)$
螺旋矩阵 II
59. 螺旋矩阵 II - 力扣(LeetCode)
给定一个正整数 n ,生成一个正方形矩阵,顺时针螺旋排列包含 1 到 n^2 所有元素
本题不涉及具体的算法,就是模拟过程,但却十分考察对代码的掌控能力
注意:
- 先用给定n除以2求出循环次数,也就是需要转几圈,若给定n为奇数,最后中间会剩一个元素,若给定n为偶数,中间不会剩元素
- 不断循环直至循环次数为0,每次循环就是一圈,完成四个边的填充,填充时遵循左闭右开的规则,每次转完一圈要更新每个边要填充的元素个数、每圈起始的横纵坐标和本圈目前填充到的横纵坐标
- 每填充一个元素,元素值就加一
- 由于循环中会递减n和循环次数,所以最后判断奇偶可以用元素值(循环结束后是n2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
func generateMatrix(n int) [][]int {
matrix := make([][]int, n)
for i := range matrix {
matrix[i] = make([]int, n)
}
count := 1 // 元素值
loop := n / 2 // 循环次数
startRow, startCol := 0, 0 // 控制起始位置
eleCount := n // 标记每圈每个边要填充的元素个数
for ; loop > 0; loop-- {
curRow, curCol := startRow, startCol
eleCount--
for ; curCol < eleCount; curCol++ {
matrix[curRow][curCol] = count // 从左到右填充排
count++
}
for ; curRow < eleCount; curRow++ {
matrix[curRow][curCol] = count // 从上到下填充列
count++
}
for ; curCol > startCol; curCol-- {
matrix[curRow][curCol] = count // 从右到左填充排
count++
}
for ; curRow > startRow; curRow-- {
matrix[curRow][curCol] = count // 从下到上填充列
count++
}
startRow++ // 更新每圈起始位置的排数
startCol++ // 更新每圈起始位置的列数
}
if n%2 == 1 {
matrix[startRow][startCol] = count
}
return matrix
}
|
螺旋矩阵
54. 螺旋矩阵 - 力扣(LeetCode)
给定一个 m 行 n 列的矩阵 matrix ,按照顺时针螺旋顺序返回矩阵中的所有元素
注意:
- 矩阵中元素不一定是从1开始的,不能用最大元素来计算循环次数,要用元素数来计算循环次数
- 每遍历完一圈查看一次结果集是否满足条件,若满足直接返回,因为是长方形时,有可能结果集已满足但循环次数还有
- 从右往左和从左往右遍历时要用偏移量控制
- 若矩阵只有一列,则直接从上往下遍历后返回,因为不构成一圈,也不能通过最后的中间遍历
- 若矩阵只有一排,则直接从左往右遍历后返回,因为最后一个元素作为四个边的哪个都不会被遍历,也会导致最后的中间遍历索引越界
- 最后剩下的中间元素,可以是一排也可能是一列,可以用总排/列数减去已遍历的排/列数来判断
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
func spiralOrder(matrix [][]int) []int {
row, col := len(matrix), len(matrix[0]) // 矩阵的最大行数和列数
res := make([]int, 0)
if col == 1 { // 只有一列
for i := range matrix {
res = append(res, matrix[i][0])
}
return res
}
if row == 1 { // 只有一列
for i := range matrix[0] {
res = append(res, matrix[0][i])
}
return res
}
count := row * col // 矩阵中元素个数
n := math.Sqrt(float64(count)) // 求元素个数的平方根
loop := int(n / 2) // 圈数(取整)
curX, curY := 0, 0 // 当前遍历到的位置
offset := 1 // 偏移量(前闭后开)
for loop > 0 { // 按圈遍历
for ; curY < col-offset; curY++ { // 从左到右遍历(该行最后一个不遍历)
res = append(res, matrix[curX][curY])
}
for ; curX < row-offset; curX++ { // 从上到下(最后一个不遍历)
res = append(res, matrix[curX][curY])
}
for ; curY >= offset; curY-- { // 从右到左(最后一个不遍历)
res = append(res, matrix[curX][curY])
}
for ; curX >= offset; curX-- { // 从下到上(最后一个不遍历)
res = append(res, matrix[curX][curY])
}
loop-- // 更新圈数
offset++ // 更新偏移量
curX++ // 更新下一次起始排数
curY++ // 更新下一次起始列数
if len(res) == count {
return res
}
}
if row-2*(offset-1) == 1 {
for ; len(res) != count; curY++ {
res = append(res, matrix[curX][curY]) // 遍历中间一排
}
} else if col-2*(offset-1) == 1 {
for ; len(res) != count; curX++ {
res = append(res, matrix[curX][curY]) // 遍历中间一列
}
}
return res
}
|
简化:loop的计算和中间值的判断
本题的loop计算与59.螺旋矩阵II算法略微差异,因为存在rows和columns两个维度,loop取min(rows, columns) / 2
中间值的判断:若min(rows, columns)为偶数,则矩阵中间不会剩下值;若min(rows, columns)为奇数,则矩阵中间会剩一个行或列;判断是行还是列,要看矩阵行数和列数的大小,如果行数大于列数,则中间剩下列,反之中间剩下行
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
func spiralOrder(matrix [][]int) []int {
row, col := len(matrix), len(matrix[0]) // 矩阵的最大行数和列数
res := make([]int, 0)
loop := min(row, col) / 2 // 圈数(取整)
curX, curY := 0, 0 // 当前遍历到的位置
offset := 1 // 偏移量(前闭后开)
for loop > 0 { // 按圈遍历
for ; curY < col-offset; curY++ { // 从左到右遍历(该行最后一个不遍历)
res = append(res, matrix[curX][curY])
}
for ; curX < row-offset; curX++ { // 从上到下(最后一个不遍历)
res = append(res, matrix[curX][curY])
}
for ; curY >= offset; curY-- { // 从右到左(最后一个不遍历)
res = append(res, matrix[curX][curY])
}
for ; curX >= offset; curX-- { // 从下到上(最后一个不遍历)
res = append(res, matrix[curX][curY])
}
loop-- // 更新圈数
offset++ // 更新偏移量
curX++ // 更新下一次起始排数
curY++ // 更新下一次起始列数
}
if min(row, col)%2 == 1 { // 奇数=>中间有剩余
if row > col { // 排数>列数=>剩余一列
for ; curX <= row-offset; curX++ { // 遍历中间一列(包括最后一个未被遍历的元素)
res = append(res, matrix[curX][curY])
}
} else { // 剩余一排
for ; curY <= col-offset; curY++ { // 遍历中间一排(包括最后一个未被遍历的元素)
res = append(res, matrix[curX][curY])
}
}
}
return res
}
|
思路三:四边界模拟(推荐)
- 空值处理: 当
matrix 为空时,直接返回空列表 [] 即可。
- 初始化: 矩阵 左、右、上、下 四个边界
l , r , t , b ,用于打印的结果列表 res 。
- 循环打印: “从左向右、从上向下、从右向左、从下向上” 四个方向循环打印。
- 根据边界打印,即将元素按顺序添加至列表
res 尾部。
- 边界向内收缩 1 (代表已被打印)。
- 判断边界是否交叉(是否打印完毕),若打印完毕则跳出。
- 返回值: 返回
res 即可。
| 打印方向 |
1. 根据边界打印 |
2. 边界向内收缩 |
3. 是否打印完毕 |
| 从左向右 |
左边界l ,右边界 r |
上边界 t 加 1 |
是否 t > b |
| 从上向下 |
上边界 t ,下边界b |
右边界 r 减 1 |
是否 l > r |
| 从右向左 |
右边界 r ,左边界l |
下边界 b 减 1 |
是否 t > b |
| 从下向上 |
下边界 b ,上边界t |
左边界 l 加 1 |
是否 l > r |
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
func spiralOrder(matrix [][]int) []int {
res := make([]int, 0)
// 初始化四边界
l, r, t, b := 0, len(matrix[0])-1, 0, len(matrix)-1
// 不断循环转圈直至相对边界交叉
for {
// 上边界的从左到右
for i := l; i <= r; i++ {
res = append(res, matrix[t][i])
}
// 上边界下移
t++
// 判边界是否交叉
if t > b {
// 循环结束
break
}
// 右边界的从上到下
for i := t; i <= b; i++ {
res = append(res, matrix[i][r])
}
// 右边界左移
r--
// 判边界是否交叉
if r < l {
// 循环结束
break
}
// 下边界的从右到左
for i := r; i >= l; i-- {
res = append(res, matrix[b][i])
}
// 下边界上移
b--
// 判边界是否交叉
if b < t {
// 循环结束
break
}
// 左边界的从下到上
for i := b; i >= t; i-- {
res = append(res, matrix[i][l])
}
// 左边界右移
l++
// 判边界是否交叉
if l > r {
// 循环结束
break
}
}
return res
}
|
- 时间复杂度:$O(mn)$
- 空间复杂度:$O(1)$
螺旋遍历二维数组
LCR 146. 螺旋遍历二维数组 - 力扣(LeetCode)
本题与上一题基本相同,唯一区别是本题数组可能为空
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
func spiralArray(array [][]int) []int {
if len(array) == 0 {
return []int{}
}
row, col := len(array), len(array[0])
res := make([]int, 0)
loop := min(row, col) / 2
curX, curY := 0, 0
offset := 1
for loop > 0 {
for ; curY < col-offset; curY++ {
res = append(res, array[curX][curY])
}
for ; curX < row-offset; curX++ {
res = append(res, array[curX][curY])
}
for ; curY >= offset; curY-- {
res = append(res, array[curX][curY])
}
for ; curX >= offset; curX-- {
res = append(res, array[curX][curY])
}
curX++
curY++
offset++
loop--
}
if min(row, col)%2 == 1 {
if row > col {
for ; curX <= row-offset; curX++ {
res = append(res, array[curX][curY])
}
} else {
for ; curY <= col-offset; curY++ {
res = append(res, array[curX][curY])
}
}
}
return res
}
|
附加
搜索二维矩阵
74. 搜索二维矩阵 - 力扣(LeetCode)
给定一个递增的整数矩阵和目标值,若在矩阵中能找到目标值,则返回 true ,否则返回 false
思路一
对每行第一个元素二分查找,找到最后一个小于目标值的元素,该行为目标行;对该行再二分查找
对两个示例分析可以发现,最后一次二分后的right就是最后一个小于目标值的元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
func searchMatrix(matrix [][]int, target int) bool {
// 对第一列二分查找
left, right := 0, len(matrix)-1
for left <= right {
mid := left + (right-left)/2
if matrix[mid][0] == target {
return true
} else if matrix[mid][0] < target {
left = mid + 1
} else {
right = mid - 1
}
}
// 索引越界
if right < 0 || right >= len(matrix) {
return false
}
// 对目标行二分查找
return search(matrix[right], target)
}
// 二分查找
func search(nums []int, target int) bool {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right-left)/2
if nums[mid] == target {
return true
} else if nums[mid] < target {
left = mid + 1
} else {
right = mid - 1
}
}
return false
}
|
- 时间复杂度:$O(logm+logn)=O(logmn)$
- 空间复杂度:$O(1)$
思路二
由于矩阵的每一行是递增的,且每行的第一个数大于前一行的最后一个数,如果把矩阵每一行拼在一起,可以得到一个递增数组
例如示例 1,三行拼在一起得a=[1,3,5,7,10,11,16,20,23,30,34,60]
由于这是一个有序数组,可以用二分查找判断target是否在matrix中
代码实现时,并不需要真的拼成一个长为mn的数组a,而是将a[i]转换成矩阵中的行号和列号。例如示例 1,i = 9对应的 a[i] = 30,由于矩阵有n = 4列,所以a[i]在⌊i/n⌋ = 2行,在i mod n = 1 列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
func searchMatrix(matrix [][]int, target int) bool {
m, n := len(matrix), len(matrix[0])
left, right := 0, m*n-1
for left <= right {
mid := left + (right-left)/2
if matrix[mid/n][mid%n] == target {
return true
} else if matrix[mid/n][mid%n] < target {
left = mid + 1
} else {
right = mid - 1
}
}
return false
}
|
- 时间复杂度:$O(logmn)$
- 空间复杂度:$O(1)$
第一个错误的版本
278. 第一个错误的版本 - 力扣(LeetCode)
给定一个整数n,0-n中从某个数开始为错误,该数后面的数到n都为错误,找出第一个错误的数,给定了判断数是否错误的API
思路:二分查找找到错误数若前一个仍为错,则继续向左查找,直到找到第一个错误的数或到首;若中间数不为错,则只需向右继续查找,因为中间不错,则左边一定不会有错
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
func firstBadVersion(n int) int {
left, right := 0, n
for left <= right {
mid := left + (right-left)/2
// 判断是否为错误版本
if isBadVersion(mid) {
// 判断是否为第一个错误版本
if mid != 0 && isBadVersion(mid) {
right = mid - 1
}
} else {
// 继续向右查找错误版本
left = mid + 1
}
}
return left
}
|
寻找旋转排序数组中的最小值
153. 寻找旋转排序数组中的最小值 - 力扣(LeetCode)
给定一个无重复元素的递增数组,该数组向右循环旋转过,返回数组中的最小值
思路:二分查找比较中间值与最后一个元素大小,若中间值大于最后一个元素,说明最小值在右半部分,反之,最小值在左半部分或中间值就是最小值
1
2
3
4
5
6
7
8
9
10
11
12
|
func findMin(nums []int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right-left)/2
if nums[mid] > nums[len(nums)-1] {
left = mid + 1
} else {
right = mid - 1
}
}
return nums[left]
}
|
寻找旋转排序数组中的最小值 II
154. 寻找旋转排序数组中的最小值 II - 力扣(LeetCode)
给定一个可能存在重复元素的递增数组,该数组向右循环旋转过,返回数组中的最小值
思路:
本题与 153 的区别在于有相同元素,这会导致在二分查找时,可能会遇到「恰好」二分元素与数组末尾元素相同的情况,此时无法确定答案在左半区间还是右半区间。
本题需要稍加修改,改为与区间右端点处的元素比较(如果写的是闭区间的话,那就是与右端点 +1 的元素比较)当二分元素与区间右端点元素相同时,既然无法确定最小值所在区间,那么干脆去掉右端点元素,继续二分,这样做不会碰巧把最小值给去掉
- 如果右端点元素就是最小值,那么
nums[mid]也是最小值,说明最小值仍然在二分区间中;
- 如果右端点元素不是最小值,这样做相当于排除了一个错误答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
func findMin(nums []int) int {
// 闭区间[0, len(nums)-2]
left, right := 0, len(nums)-2
for left <= right {
mid := left + (right-left)/2
// 比较中间值与右端点+1
if nums[mid] > nums[right+1] {
left = mid + 1
} else if nums[mid] < nums[right+1] {
right = mid - 1
} else {
// 去掉右端点
right--
}
}
return nums[left]
}
|
搜索旋转排序数组
33. 搜索旋转排序数组 - 力扣(LeetCode)
给定一个无重复元素的递增数组和目标值,该数组向右循环旋转过,返回数组中目标值的下标,不存在返回-1
思路:先二分找最小值下标(轴点),再取模正常二分找目标值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
func search(nums []int, target int) int {
findMinIdx := func() int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right-left)/2
if nums[mid] > nums[len(nums)-1] {
left = mid + 1
} else {
right = mid - 1
}
}
return left
}
minIdx := findMinIdx()
fmt.Println(minIdx)
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right-left)/2
afterMidIdx := (mid + minIdx) % len(nums)
if nums[afterMidIdx] == target {
return afterMidIdx
} else if nums[afterMidIdx] > target {
right = mid - 1
} else {
left = mid + 1
}
}
return -1
}
|
搜索旋转排序数组 II
81. 搜索旋转排序数组 II - 力扣(LeetCode)
给定一个可能存在重复元素的递增数组和目标值,该数组向右循环旋转过,若数组中存在目标值返回true,否则返回false
思路:先二分找最小值下标(轴点),再取模正常二分找目标值。
注意:找轴点时,若最小值重复,要找到旋转前的首个最小值(轴点)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
func search(nums []int, target int) bool {
// 二分查找最小值索引
minIdx := findMin(nums)
// 找第一个min
if minIdx == 0 && nums[minIdx] == nums[len(nums)-1] {
// 首和尾相同都是最小值,更新最小值为首的前一个(尾)
minIdx = len(nums) - 1
}
// 从尾向前找第一个最小值(轴点)
for minIdx != 0 && nums[minIdx-1] == nums[minIdx] {
// 更新最小值为前一个
minIdx--
}
// 二分查找目标值
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right-left)/2
// afterMidIdx是映射回数组的mid
afterMidIdx := (mid + minIdx) % len(nums)
if nums[afterMidIdx] == target {
return true
} else if nums[afterMidIdx] > target {
right = mid - 1
} else {
left = mid + 1
}
}
return false
}
func findMin(nums []int) int {
left, right := 0, len(nums)-2
for left <= right {
mid := left + (right-left)/2
if nums[mid] > nums[right+1] {
left = mid + 1
} else if nums[mid] < nums[right+1] {
right = mid - 1
} else {
right--
}
}
return left
}
|
附加
字符串的排列
567. 字符串的排列 - 力扣(LeetCode)
给定两个字符串s1和s2,判断s1的排列之一是否为s2的子串
思路:维护一个大小为2的滑动窗口
实现细节:
- 用两个数组分别记录两个字符串中各字符的个数,若相等,直接返回
true
- 初始化窗口大小为
len(s1),初始化时只移动右边界,此后左右边界同时移动,同时不断更新两个数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
func checkInclusion(s1 string, s2 string) bool {
if len(s1) > len(s2) {
return false
}
cnt1, cnt2 := [26]int{}, [26]int{}
// 初始化窗口
for i, v := range s1 {
cnt1[v-'a']++
cnt2[s2[i]-'a']++
}
if cnt1 == cnt2 {
return true
}
// 遍历s2
for i := len(s1); i < len(s2); i++ {
cnt2[s2[i-len(s1)]-'a']--
cnt2[s2[i]-'a']++
if cnt1 == cnt2 {
return true
}
}
return false
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
无重复字符的最长子串
3. 无重复字符的最长子串 - 力扣(LeetCode)
给定一个字符串,求其中不含有重复字符的最长子串的长度
思路:维护一个无重复元素的滑动窗口,初始化左边界指向首,右边界不断向右移动,若遇到字符与窗口内字符重复,则将左边界向右移动到窗口内重复字符的下一个字符;每次右边界移动都记录窗口内的字符并更新目前最长子串长度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
func lengthOfLongestSubstring(s string) int {
res := 0
// 标记窗口内字符
cnt := [128]bool{}
// 左边界初始化指向首
left := 0
// 右边界遍历字符串
for right, ch := range s {
// 循环判当前字符与窗口内是否重复
for cnt[ch] {
// 删除当前左边界对应字符的标记
cnt[s[left]] = false
// 左边界右移
left++
}
// 标记当前字符
cnt[ch] = true
// 更新目前最长子串长度
res = max(res, right-left+1)
}
return res
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
区间和
卡码网:58. 区间和
给定一个整数数组 Array和若干区间,返回该数组在每个指定区间内元素的总和
暴力时间复杂度:,n为元素个数,m为查询次数,每次查询全区间,最坏为$O(n*m)$
前缀和:
p[i]:array[0]到array[i]的和- 计算
array[3] + array[4] + array[5] = p[5] - p[2]
注意:Go语言中fmt.Scan的读操作效率低,可以使用bufio.Scanner来提升输入性能,避免超时错误
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
package main
import (
"fmt"
"bufio"
"os"
"strconv"
)
func main() {
scanner := bufio.NewScanner(os.Stdin)
// 读取数组长度
scanner.Scan()
length, _ := strconv.Atoi(scanner.Text())
// 读取数组元素
array := make([]int, length)
for i := 0; i < length; i++ {
scanner.Scan()
array[i], _ = strconv.Atoi(scanner.Text())
}
// 原数组上求前缀和
for i := 1; i < len(array); i++ {
array[i] += array[i-1]
}
// 循环读取区间直到EOF
var left, right int
for scanner.Scan() {
fmt.Sscanf(scanner.Text(), "%d %d", &left, &right)
// 判断区间左端是否为0
if left == 0 {
// 区间左端为0直接输出前缀和
fmt.Println(array[right])
} else {
// 用前缀和求区间和
fmt.Println(array[right]-array[left-1])
}
}
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
开发商购买土地
卡码网:44. 开发商购买土地
给定一个矩形区域,返回将该区域分为两部分的最小差值
逐行划分、逐列划分,不断比较求得最小结果
求差值可用sum-2*a:a+b=c=>b=c-a=>a-b = a-c+a = 2a - c
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
package main
import (
"fmt"
"math"
)
func main() {
// 读取矩形长宽
var n, m int
fmt.Scanln(&n, &m)
// 读取矩形
array := make([][]int, n)
for i := range array {
array[i] = make([]int, m)
}
sum := 0
for i := 0; i < n; i++ {
for j := 0; j < m; j++ {
fmt.Scan(&array[i][j])
sum += array[i][j]
}
}
res := math.MaxInt32
count := 0
// 按行切分
for i := 0; i < n; i++ {
for j := 0; j < m; j++ {
count += array[i][j]
// 判断是否到行尾
if j == m-1 {
// 求得从当前行切分的差值
res = min(res, max(sum, 2*count)-min(sum, 2*count))
}
}
}
count = 0
// 按列切分
for j := 0; j < m; j++ {
for i := 0; i < n; i++ {
count += array[i][j]
// 判断是否到列尾
if i == n-1 {
// 求得从当前列切分的差值
res = min(res, max(sum, 2*count)-min(sum, 2*count))
}
}
}
fmt.Println(res)
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
有多少小于当前数字的数字
1365. 有多少小于当前数字的数字 - 力扣(LeetCode)
给定一个数组,对于其中每个元素,统计数组中比它小的元素的个数
思路:
- 复制一份原数组进行排序,用哈希存储排序后数组每个元素前面有多少个元素;
- 由于哈希key的唯一性,从后向前遍历排序后数组,可以保证遇到重复元素时记录到最左边元素前的元素个数
- 遍历原数组,在哈希中查询得到该元素前的元素个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
func smallerNumbersThanCurrent(nums []int) []int {
// 复制原数组
temp := make([]int, len(nums))
copy(temp, nums)
// 数组排序
sort.Ints(temp)
// 初始化哈希表
mp := make(map[int]int)
// 倒序遍历排序后数组
for i := len(temp) - 1; i >= 0; i-- {
// 哈希表存储k:元素 v:比该元素小的元素个数
mp[temp[i]] = i
}
// 遍历原数组
for i := 0; i < len(nums); i++ {
// 直接在原数组上存储比当前元素小的元素个数
nums[i] = mp[nums[i]]
}
return nums
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(n)$
有效的山脉数组
941. 有效的山脉数组 - 力扣(LeetCode)
给定一个数组,判断其是否为山脉数组
山脉数组:数组长度大于等于3,有一个顶点,严格递增到顶点(无重复),从顶点开始严格递减
思路一:状态切换
- 数组长度小于3,返回
false
- 用一个变量记录是否为上升态,初始化为上升态,若上升态遇到当前元素等于下一元素,返回
false
- 直到当前元素大于下一个元素,判断是否从索引0就切换,若是,说明单调减,返回
false,若不是,变为非上升态
- 若非上升态遇到当前元素小于等于下一个元素,返回
false
- 遍历结束后判断上升态是否持续到最后一个元素,若是,说明单调增,返回
false
- 最后返回
true
注意:判断单调情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
func validMountainArray(arr []int) bool {
// 判断数组长度是否小于3
if len(arr) < 3 {
return false
}
// 初始化为上升态
isInc := true
// 遍历数组
i := 0
for ; i < len(arr)-1; i++ {
// 判断当前元素是否等于下一元素
if arr[i] == arr[i+1] {
return false
}
// 判断是否为上升态
if isInc {
// 判断当前元素是否大于下一元素
if arr[i] > arr[i+1] {
// 判断是否从索引0就切换为非上升态
if i == 0 {
return false
}
// 切换为非上升态
isInc = false
}
} else {
// 判断当前元素是否小于下一元素
if arr[i] < arr[i+1] {
return false
}
}
}
// 判断上升态是否持续到最后一个元素
if isInc {
return false
}
return true
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
思路二:双指针
- 用两个指针分别指向数组首尾
- 若左指针指向元素小于后一元素,则后移一个单位;若右指针指向元素小于前一元素,则前移一个单位
- 若左右指针在非首尾位置相遇,则返回
true;若在首尾处相遇说明是单调,返回false
注意:不能在一个循环中同时移动左右指针并且判断是否相遇,因为在非山脉的情况下,左右指针永远不会相遇,导致进入死循环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
func validMountainArray(arr []int) bool {
if len(arr) < 3 {
return false
}
// 初始化左右指针分别指向首尾
left, right := 0, len(arr)-1
// 移动左指针到最终位置
for left != len(arr)-1 && arr[left] < arr[left+1] {
left++
}
// 移动右指针到最终位置
for right != 0 && arr[right] < arr[right-1] {
right--
}
// 判断左右指针是否相遇且在非首尾处
if left == right && left != len(arr)-1 && right != 0 {
return true
}
return false
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
独一无二的出现次数
1207. 独一无二的出现次数 - 力扣(LeetCode)
给定一个整数数组,若数组中每个数的出现次数都是独一无二的,则返回 true;否则返回 false
思路:遍历数组,用字典记录出现次数;最后遍历字典值,用另一字典记录是否有重复,若遇到重复出现的,则返回false,遍历结束返回true
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
func uniqueOccurrences(arr []int) bool {
mp1 := make(map[int]int)
mp2 := make(map[int]bool)
// 遍历给定数组统计每个数的出现次数
for _, v := range arr {
mp1[v]++
}
// 遍历字典检查出现次数是否重复
for _, v := range mp1 {
// 判断是否在字典中已出现该次数
if mp2[v] {
return false
}
// 标记该次数出现过
mp2[v] = true
}
return true
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(n)$
由于题目给定了数组大小和元素值范围,所以可以用数组做哈希
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
func uniqueOccurrences(arr []int) bool {
// 统计次数
mp1 := [2001]int{}
// 标记是否出现过
mp2 := [1001]bool{}
// 遍历给定数组统计每个数的出现次数
for _, v := range arr {
mp1[v+1000]++
}
// 遍历字典检查出现次数是否重复
for _, v := range mp1 {
// 判断是否在字典中已出现该次数
if v != 0 && mp2[v] {
return false
}
// 标记该次数出现过
mp2[v] = true
}
return true
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(n)$
轮转数组
189. 轮转数组 - 力扣(LeetCode)
给定一个整数数组,将数组中的元素向右轮转 k 个位置,其中 k 是非负数
思路一:暴力
新开辟一个数组,将原数组轮换后的元素值存入新数组,最后把新数组拷贝回原数组
1
2
3
4
5
6
7
|
func rotate(nums []int, k int) {
temp := make([]int, len(nums))
for i, v := range nums {
temp[(i+k%len(nums))%len(nums)] = v
}
copy(nums, temp)
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(n)$
思路二:原地轮转
将被轮转替换的元素交换到未排定数组首保存,每次都将当前操作元素与未排定数组首交换
注意:当轮转后元素为未排定的数组首时,说明未排定元素首和当前操作元素都已排定,无需轮换,只更新当前操作元素与未排定数组首即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
func rotate(nums []int, k int) {
// 当前操作的元素索引
cur := 0
// 未排定的数组首
temp := 0
// 循环len(nums)次保证每个元素都轮转
for i := 0; i < len(nums); i++ {
// 轮转后的索引
after := (cur + k) % len(nums)
// 判断轮转后元素是否为未排定的数组首
if after == temp {
// 更新当前操作元素为未排定的数组首下一个元素
cur = after + 1
// 更新未排定的数组首
temp++
// 跳过本次循环后续
continue
}
// 被替换元素放至未排定的数组首
nums[temp], nums[after] = nums[after], nums[temp]
// 更新当前操作的元素索引
cur = after
}
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
思路三:反转
- 反转整个字符串
- 反转区间为前k的子串
- 反转区间为k到末尾的子串
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
func rotate(nums []int, k int) {
// 约束k不越界
k = k % len(nums)
// 整体反转
reverse(nums)
// 反转前k
reverse(nums[:k])
// 反转k到末尾
reverse(nums[k:])
}
func reverse(nums []int) {
for left, right := 0, len(nums)-1; left < right; left, right = left+1, right-1 {
nums[left], nums[right] = nums[right], nums[left]
}
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
寻找数组的中心下标
724. 寻找数组的中心下标 - 力扣(LeetCode)
给定一个整数数组,返回中心下标,中心下标左侧所有元素相加的和等于右侧所有元素相加的和,若不存在中心下标,则返回 -1
思路一:先统计出前i位的和,最后遍历数组,用前i位总和减去第i位元素值得到左侧所有元素和,用所有元素和减去前i位总和得到右侧所有元素和,若相等,则说明找到中心下标,直接返回
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
func pivotIndex(nums []int) int {
sum := make([]int, len(nums))
// 统计前i位的和
sum[0] = nums[0]
for i := 1; i < len(nums); i++ {
sum[i] = sum[i-1] + nums[i]
}
// 遍历给定数组和总和数组
for i, v := range nums {
// 判断当前元素之前的所有元素和是否等于之后的所有元素和
if sum[i]-v == sum[len(sum)-1]-sum[i] {
// 返回当前索引
return i
}
}
return -1
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(n)$
思路二:先统计出总和,最后遍历数组,逐个累加得到前i位总和,同时用总和减去前i位总和再加上当前元素值得到包括第i位在内的之后所有元素和,若相等,则说明当前索引为中心下标,直接返回
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
func pivotIndex(nums []int) int {
sum := 0
// 统计总和
for _, v := range nums {
sum += v
}
leftSum := 0
// 遍历给定数组
for i, v := range nums {
leftSum += v
rightSum := sum - leftSum + v
// 判断前i位所有元素和是否等于包括第i位在内的之后的所有元素和
if leftSum == rightSum {
// 返回当前索引
return i
}
}
return -1
}
|
思路三:前后缀和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
func pivotIndex(nums []int) int {
res := -1
preSum := 0
for _, v := range nums {
preSum += v
}
sufSum := 0
for i := len(nums) - 1; i >= 0; i-- {
preSum -= nums[i]
if preSum == sufSum {
res = i
}
sufSum += nums[i]
}
return res
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
按奇偶排序数组 II
922. 按奇偶排序数组 II - 力扣(LeetCode)
给定一个非负整数数组, 其中一半整数是奇数 ,一半整数是偶数;对数组进行排序,以便当nums[i]为奇数时,i也是奇数 ;当nums[i]为偶数时,i也是 偶数
思路:遍历所有偶数位,若遇到奇数,则在奇数位中找到一个偶数交换
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
func sortArrayByParityII(nums []int) []int {
// 标记目前遍历到的奇数位
oddIdx := 1
// 遍历偶数位
for i := 0; i < len(nums); i += 2 {
// 判断是否为奇数
if nums[i]%2 != 0 {
// 遍历奇数位找到一个偶数
for nums[oddIdx]%2 != 0 {
oddIdx += 2
}
// 交换
nums[i], nums[oddIdx] = nums[oddIdx], nums[i]
}
}
return nums
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
下一个排列
31. 下一个排列 - 力扣(LeetCode)
给定一个整数数组,找出该数组的下一个排列,必须原地修改,只允许使用额外常数空间
思路:要找下一个排列,则需要满足
- 下一个排列比当前数大:将后面的大数与前面的小数交换
- 下一个排列增加的幅度尽可能的小:在尽可能靠右的低位交换,交换后需要将大叔后面的所有数重置为升序,因为升序排列就是最小的排列
实现:从后向前找第一对升序的数,交换值,然后将交换后大数后面的所有数重排为升序;若遍历结束都没有找到升序,说明整个数组为最大排列,只需反转即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
func nextPermutation(nums []int) {
// 从后向前遍历
for i := len(nums) - 1; i >= 0; i-- {
for j := len(nums) - 1; j > i; j-- {
// 判断是否为升序
if nums[i] < nums[j] {
// 大小数交换值
nums[i], nums[j] = nums[j], nums[i]
// 重排大数后所有元素
sort.Ints(nums[i+1:])
return
}
}
}
// 重排整个降序数组为升序
sort.Ints(nums)
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
盛最多水的容器
11. 盛最多水的容器 - 力扣(LeetCode)
接雨水给定容器是宽度为1的柱子,而本题给定容器是宽度为0的线,问最多能盛多少水
思路:可容纳水的高度由两板中的 短板 决定,在每个状态下,无论长板或短板向中间收窄一格,都会导致水槽 底边宽度 −1 变短:
- 若向内移动 短板 ,水槽的短板 min(h[i],h[j]) 可能变大,因此下个水槽的面积 可能增大 。
- 若向内移动 长板 ,水槽的短板 min(h[i],h[j]) 不变或变小,因此下个水槽的面积 一定变小
因此,初始化双指针分列水槽左右两端,循环每轮将短板向内移动一格,并更新面积最大值,直到两指针相遇时跳出;即可获得最大面积
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
func maxArea(height []int) int {
res := 0
// 初始化双指针指向两端,移动短板,直到左右指针相遇
for left, right := 0, len(height)-1; left < right; {
// 判断短板是否为左
if height[left] < height[right] {
// 更新结果:计算面积后比较
res = max(res, height[left]*(right-left))
// 移动短板
left++
} else {
res = max(res, height[right]*(right-left))
// 移动短板
right--
}
}
return res
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
除自身以外数组的乘积
238. 除自身以外数组的乘积 - 力扣(LeetCode)
给定一个整数数组,返回数组中每个元素除自身之外其余各元素的乘积,题目数据 保证 数组中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。请 **不要使用除法,**且在 O(n) 时间复杂度内完成此题
思路:先统计出每个元素除自身以外的后缀积,再边计算前缀积,边用后缀积计算当前元素除自身以外的其余各元素的乘积,结果存入后缀积,最后后缀积容器中保存的即为结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
// 写法一
func productExceptSelf(nums []int) []int {
// 记录除自身以外的后缀积
suf := make([]int, len(nums))
// 初始化后缀积的尾元素
suf[len(nums)-1] = 1
// 记录除自身以外的前缀积
pre := 1
// 倒序遍历数组
for i := len(nums) - 2; i >= 0; i-- {
// 计算并记录后缀积
suf[i] = suf[i+1] * nums[i+1]
}
// 遍历数组
for i, v := range nums {
// 计算除自身以外数组的乘积
suf[i] *= pre
// 计算并记录前缀积
pre *= v
}
return suf
}
// 写法二
func productExceptSelf(nums []int) []int {
res := make([]int, len(nums))
// 前缀积
copy(res, nums)
for i := 1; i < len(nums)-1; i++ {
res[i] *= res[i-1]
}
// 末元素为之前的前缀积
res[len(res)-1] = res[len(res)-2]
// 倒序遍历
for i := len(nums) - 2; i >= 1; i-- {
// 前缀积*后缀积
res[i] = res[i-1] * nums[i+1]
// 后缀积
nums[i] *= nums[i+1]
}
// 首元素为之后的后缀积
res[0] = nums[1]
return res
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
缺失的第一个正数
41. 缺失的第一个正数 - 力扣(LeetCode)
给定一个未排序的整数数组,返回其中没有出现的最小的正整数。要求是时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案
思路一:快排后暴力枚举各种情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
func firstMissingPositive(nums []int) int {
// 升序重排
sort.Ints(nums)
for i := range nums {
if i == 0 && nums[i] > 1 {
// 首位大于1,直接返回1
return 1
} else if i == len(nums)-1 {
if nums[i] >= 0 {
// 末位为正整数,直接返回下一个数
return nums[i] + 1
}
// 末位为负数或0,直接返回1
return 1
} else if nums[i] == nums[i+1] {
// 去重
continue
} else if nums[i] <= 0 && nums[i+1] > 1 {
// 当前位为负数或0且下一位直接大于1,直接返回1
return 1
} else if nums[i] > 0 && nums[i+1] != nums[i]+1 {
// 当前位为正数且下一位跳变,直接返回当前位下一个数
return nums[i] + 1
}
}
return 1
}
|
- 时间复杂度:$O(nlogn)$
- 空间复杂度:$O(1)$
思路二:原地构建哈希表
对于一个长度为 N 的数组,其中没有出现的最小正整数只能在 [1,N+1] 中。这是因为如果 [1,N] 都出现了,那么答案是 N+1,否则答案是 [1,N] 中没有出现的最小正整数。这样一来,我们将所有在 [1,N] 范围内的数放入哈希表,也可以得到最终的答案。而给定的数组恰好长度为 N,这让我们有了一种将数组设计成哈希表的思路:
我们对数组进行遍历,对于遍历到的数 x,如果它在 [1,N] 的范围内,那么就将数组中的第 x−1 个位置(注意:数组下标从 0 开始)打上「标记」。在遍历结束之后,如果所有的位置都被打上了标记,那么答案是 N+1,否则答案是最小的没有打上标记的位置加 1。
那么如何设计这个「标记」呢?由于数组中的数没有任何限制,因此这并不是一件容易的事情。但我们可以继续利用上面的提到的性质:由于我们只在意 [1,N] 中的数,因此我们可以先对数组进行遍历,把不在 [1,N] 范围内的数修改成任意一个大于 N 的数(例如 N+1)。这样一来,数组中的所有数就都是正数了,因此我们就可以将「标记」表示为「负号」。算法的流程如下:
- 我们将数组中所有小于等于 0 的数修改为 N+1;
- 我们遍历数组中的每一个数 x,它可能已经被打了标记,因此原本对应的数为 ∣x∣,其中 ∣∣ 为绝对值符号。如果 ∣x∣∈[1,N],那么我们给数组中的第 ∣x∣−1 个位置的数添加一个负号。注意如果它已经有负号,不需要重复添加;
- 在遍历完成之后,如果数组中的每一个数都是负数,那么答案是 N+1,否则答案是第一个正数的位置加 1
注意:要用绝对值,因为后面的元素值可能还没遍历到就被标记为负数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
func firstMissingPositive(nums []int) int {
// 遍历数组去掉非正数
for i, v := range nums {
if v <= 0 {
// 将非正数全部改成N+1
nums[i] = len(nums) + 1
}
}
// 遍历数组标记出现的1-N之间所有正数
for _, v := range nums {
// 负值取绝对值
if v < 0 {
v = -v
}
// 判该值是否位于1-N之间
if v < len(nums)+1 {
// 判是否已被标记
if nums[v-1] > 0 {
// 用负值标记对应位置,表示1-N中存在该数
nums[v-1] = -nums[v-1]
}
}
}
// 遍历哈希表找出1-N中缺失的第一个正数
for i, v := range nums {
if v > 0 {
// 该位置的值未被标记,说明该位置+1的数缺失,直接返回
return i + 1
}
}
// 1-N都未缺失,返回N+1
return len(nums) + 1
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
思路三:交换
除了打标记以外,我们还可以使用置换的方法,将给定的数组「恢复」成下面的形式:
如果数组中包含 x∈[1,N],那么恢复后,数组的第 x−1 个元素为 x。
在恢复后,数组应当有 [1, 2, ..., N] 的形式,但其中有若干个位置上的数是错误的,每一个错误的位置就代表了一个缺失的正数。以题目中的示例二 [3, 4, -1, 1] 为例,恢复后的数组应当为 [1, -1, 3, 4],我们就可以知道缺失的数为 2
对于遍历到的数 x=nums[i],如果 x∈[1,N],我们就知道 x 应当出现在数组中的 x−1 的位置,因此交换 nums[i] 和 nums[x−1],这样 x 就出现在了正确的位置。在完成交换后,新的 nums[i] 可能还在 [1,N] 的范围内,我们需要继续进行交换操作,直到 x不在[1,N]中
由于每次的交换操作都会使得某一个数交换到正确的位置,因此交换的次数最多为 N,整个方法的时间复杂度为 O(N)
注意:避免原地交换陷入死循环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
func firstMissingPositive(nums []int) int {
// 遍历数组将正数放在1-N对应位置
for i := range nums {
// 循环判断当前值是否在1-N中且对应位置值不等于当前值
for nums[i] > 0 && nums[i] <= len(nums) && nums[nums[i]-1] != nums[i] {
// 交换当前值至对应位置
nums[nums[i]-1], nums[i] = nums[i], nums[nums[i]-1]
}
}
// 遍历数组找与1-N不对应得值
for i, v := range nums {
if v != i+1 {
return i + 1
}
}
// 1-N都有,返回N+1
return len(nums) + 1
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
矩阵置零
73. 矩阵置零 - 力扣(LeetCode)
给定一个矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 ,要求算法空间复杂度为O(1)
思路一:标记使用两个一维数组
用两个标记数组分别记录每一行和每一列是否有零出现。具体地,先遍历该数组一次,如果某个元素为 0,那么就将该元素所在的行和列所对应标记数组的位置置为 true。最后再次遍历该数组,用标记数组更新原数组即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
func setZeroes(matrix [][]int) {
row := make([]bool, len(matrix))
col := make([]bool, len(matrix[0]))
for i := range matrix {
for j := range matrix[i] {
if matrix[i][j] == 0 {
row[i], col[j] = true, true
}
}
}
for i := range matrix {
for j := range matrix[i] {
if row[i] || col[j] {
matrix[i][j] = 0
}
}
}
}
|
- 时间复杂度:$O(mn)$
- 空间复杂度:$O(m+n)$
思路二:使用两个标记变量
用矩阵的第一行和第一列代替方法一中的两个标记数组,以达到 O(1) 的额外空间。但这样会导致原数组的第一行和第一列被修改,无法记录它们是否原本包含 0。因此需要额外使用两个标记变量分别记录第一行和第一列是否原本包含 0
在实际代码中,首先预处理出两个标记变量,接着使用其他行与列去处理第一行与第一列,然后反过来使用第一行与第一列去更新其他行与列,最后使用两个标记变量更新第一行与第一列即可
注意:置0时仍要从第二行第二列遍历矩阵根据第一排第一列置0,因为第一排第一列保存的状态此时还不能改变
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
func setZeroes(matrix [][]int) {
// 记录第一行第一列是否存在0元素
row0, col0 := false, false
// 遍历第一行查找0元素
for _, v := range matrix[0] {
if v == 0 {
// 标记
row0 = true
break
}
}
// 遍历第一列查找0元素
for _, v := range matrix {
if v[0] == 0 {
// 标记
col0 = true
break
}
}
// 从第二行第二列遍历矩阵查找0元素
for i := 1; i < len(matrix); i++ {
for j := 1; j < len(matrix[0]); j++ {
if matrix[i][j] == 0 {
// 计入对应第一排第一列
matrix[0][j], matrix[i][0] = 0, 0
}
}
}
// 从第二行第二列遍历矩阵根据第一排第一列置0
for i := 1; i < len(matrix); i++ {
for j := 1; j < len(matrix[0]); j++ {
if matrix[i][0] == 0 || matrix[0][j] == 0 {
matrix[i][j] = 0
}
}
}
// 判断第一排本身原来是否含0
if row0 {
// 第一排置0
for j := range matrix[0] {
matrix[0][j] = 0
}
}
// 判断第一列本身原来是否含0
if col0 {
// 第一列置0
for i := range matrix {
matrix[i][0] = 0
}
}
}
|
- 时间复杂度:$O(mn)$
- 空间复杂度:$O(1)$
旋转图像
48. 旋转图像 - 力扣(LeetCode)
给定一个 n × n 的二维矩阵,请将图像顺时针旋转 90 度,要求必须原地旋转
思路一:四边界按圈旋转
先保存右边界,再上转右,左转上,下转左,最后保存的右转下,每转完一圈,移动四边界,边界相遇或交叉说明旋转完成
- 注意:必须初始化声明temp的长度,再用矩阵索引和temp索引一一对应存值;因为在向内层循环后取值时,矩阵索引不一定从0开始,若从0开始忘temp存,会越界
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
func rotate(matrix [][]int) {
temp := make([]int, len(matrix))
l, r, t, b := 0, len(matrix)-1, 0, len(matrix)-1
for {
// 保存右
for i := t; i <= b; i++ {
temp[i] = matrix[i][r]
}
// 上到右倒序
for i := r; i >= l; i-- {
matrix[i][r] = matrix[t][i]
}
// 左到上顺序
for i := t; i <= b; i++ {
matrix[t][len(matrix)-i-1] = matrix[i][l]
}
// 下到左顺序
for i := l; i <= r; i++ {
matrix[i][l] = matrix[b][i]
}
// 右到下顺序
for i := t; i <= b; i++ {
matrix[b][len(matrix)-i-1] = temp[i]
}
// 移动边界
l, r, t, b = l+1, r-1, t+1, b-1
if l >= r || t >= b {
break
}
}
}
|
- 时间复杂度:$O(n^2)$
- 空间复杂度:$O(n)$
思路二:单个元素旋转
一轮可以完成矩阵 4 个元素的旋转。因而,只要分别以矩阵左上角 1/4 的各元素为起始点执行旋转操作,即可完整实现矩阵旋转
具体来看,当矩阵大小 n 为偶数时,取前 $\frac{n}{2}$ 行、前 $\frac{n}{2}$ 列的元素为起始点;当矩阵大小 n 为奇数时,取前 $\frac{n}{2}$ 行、前 $\frac{n+1}{2}$ 列的元素为起始点。由于(偶数+1)/2值与偶数/2值一样,所有统一取前 $\frac{n}{2}$ 行和前 $\frac{n+1}{2}$ 列
注意:找规律时,用行列不相等的上作为基准,推导出其他三个方向的坐标,每个坐标中 i 和 j 都会用到
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
func rotate(matrix [][]int) {
for i := 0; i < len(matrix)/2; i++ {
for j := 0; j < (len(matrix)+1)/2; j++ {
// 保存右
temp := matrix[j][len(matrix)-i-1]
// 上转右
matrix[j][len(matrix)-i-1] = matrix[i][j]
// 左转上
matrix[i][j] = matrix[len(matrix)-j-1][i]
// 下转左
matrix[len(matrix)-j-1][i] = matrix[len(matrix)-i-1][len(matrix)-j-1]
// 右转下
matrix[len(matrix)-i-1][len(matrix)-j-1] = temp
}
}
}
|
- 时间复杂度:$O(n^2)$
- 空间复杂度:$O(1)$
搜索二维矩阵 II
240. 搜索二维矩阵 II - 力扣(LeetCode)
编写一个高效的算法来搜索 m x n 矩阵中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列
- 每列的元素从上到下升序排列
思路一:根据排首和排尾确定目标值在该排范围内后,二分查找该排
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
func searchMatrix(matrix [][]int, target int) bool {
for _, row := range matrix {
if row[0] <= target && row[len(matrix[0])-1] >= target {
if row[0] == target || row[len(matrix[0])-1] == target {
return true
}
// 二分查找
left, right := 0, len(matrix[0])-1
for left <= right {
mid := left + (right-left)/2
if row[mid] == target {
return true
} else if row[mid] < target {
left = mid + 1
} else {
right = mid - 1
}
}
}
}
return false
}
|
- 时间复杂度:$O(mlogn)$
- 空间复杂度:$O(1)$
思路二:切割法
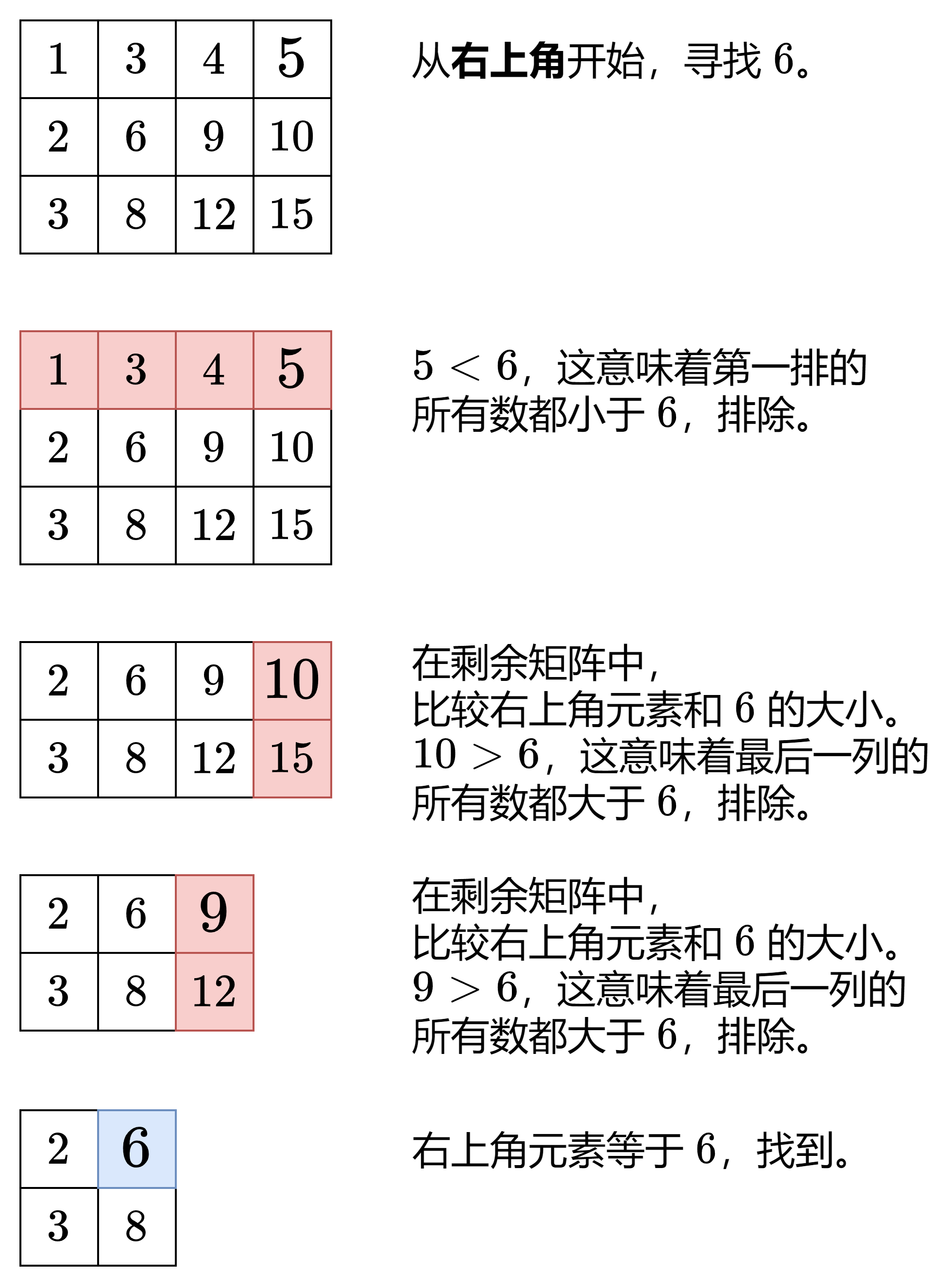
从右上角开始,比较右上角元素与目标值,若小于目标值,排除该排,若大于目标值,排除该列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
func searchMatrix(matrix [][]int, target int) bool {
row, col := 0, len(matrix[0])-1
for row < len(matrix) && col >= 0 {
if matrix[row][col] == target {
return true
} else if matrix[row][col] < target {
// 去除该排
row++
} else {
// 去除该列
col--
}
}
return false
}
|
- 时间复杂度:$O(m+n)$
- 空间复杂度:$O(1)$
最佳观光组合
1014. 最佳观光组合 - 力扣(LeetCode)
给定一个正整数数组 values,其中 values[i] 表示第 i 个观光景点的评分,并且两个景点 i 和 j 之间的 距离 为 j - i。一对景点(i < j)组成的观光组合的得分为 values[i] + values[j] + i - j ,也就是景点的评分之和 减去 它们两者之间的距离。返回一对观光景点能取得的最高分
思路:枚举右,维护左;可以将得分公式,拆分成 values[i]+i 和 values[j]−j 两部分,这样对于统计景点 j 答案的时候,由于 values[j]−j 是固定不变的,因此最大化 values[i]+i+values[j]−j 的值其实就等价于求 [0, j−1] 中 values[i]+i 的最大值 mx,景点 j 的答案即为 mx+values[j]−j 。而 mx 的值只要从前往后遍历 j 的时候同时维护即可,这样每次遍历到景点 j 的时候,寻找使得得分最大的 i 就能从 O(n) 降至 O(1) 的时间复杂度,总时间复杂度就能从 O(n^2) 降至 O(n)
1
2
3
4
5
6
7
8
|
func maxScoreSightseeingPair(values []int) int {
res, mx := 0, 0
for j, v := range values {
res = max(res, mx+v-j)
mx = max(mx, j+v)
}
return res
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
寻找两个正序数组的中位数
4. 寻找两个正序数组的中位数 - 力扣(LeetCode)
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。找出并返回这两个正序数组的 中位数 。算法的时间复杂度应该为 O(log (m+n))
思路一:二分查找
假设两个有序数组的长度分别为 m 和 n,根据中位数的定义,当 m+n 是奇数时,中位数是两个有序数组中的第 (m+n)/2+1 个元素,当 m+n 是偶数时,中位数是两个有序数组中的第 (m+n)/2 个元素和第 (m+n)/2+1 个元素的平均值。因此,这道题可以转化成寻找两个有序数组中的第 k 小的数,其中 k 为 (m+n)/2 或 (m+n)/2+1
假设两个有序数组分别是 A 和 B。要找到第 k 个元素,可以比较 A[k/2−1] 和 B[k/2−1]
-
如果 A[k/2−1]<B[k/2−1],则比 A[k/2−1] 小的数最多只有 A 的前 k/2−1 个数和 B 的前 k/2−1 个数,即比 A[k/2−1] 小的数最多只有 k−2 个,因此 A[k/2−1] 一定不可能是第 k 小的数,所以 A[0] 到 A[k/2−1]可以全部排除
-
如果 A[k/2−1]>B[k/2−1],则可以排除 B[0] 到 B[k/2−1]
-
如果 A[k/2−1]=B[k/2−1],则可以归入第一种情况处理
因此,查找范围缩小了一半。此后,在排除后的新数组上继续进行二分查找,并且根据排除数的个数,减小 k 的值
- 若 A[k/2−1] 或者 B[k/2−1] 越界,选取对应数组中的最后一个元素,最后根据排除数的个数减小 k 的值
- 若一个数组为空,说明该数组中的所有元素都被排除,直接返回另一个数组中第 k 小的元素即可
- 若 k=1,直接返回两个数组首元素的最小值即可
注意:找第k小元素,从0计的话会出错
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {
totalLength := len(nums1) + len(nums2)
// 判总长度是否为奇数
if totalLength%2 != 0 {
// 返回第totalLength/2+1小(从1计)
return float64(getKth(nums1, nums2, totalLength/2+1))
} else {
// 返回第totalLength/2小和第totalLength/2+1小的平均值(从1计)
return float64((getKth(nums1, nums2, totalLength/2) + getKth(nums1, nums2, totalLength/2+1))) / 2
}
}
func getKth(nums1, nums2 []int, k int) int {
for {
// 判nums1是否无元素
if len(nums1) == 0 {
// 直接返回当前nums2的第k小
return nums2[k-1]
}
if len(nums2) == 0 {
return nums1[k-1]
}
// 判是否需要找第1小元素
if k == 1 {
// 返回nums1和nums2首元素中的小值
return min(nums1[0], nums2[0])
}
// 判nums1和nums2的k/2-1位置是否越界 若越界则指向最后一个元素
idx1 := min(k/2-1, len(nums1)-1)
idx2 := min(k/2-1, len(nums2)-1)
// 判nums1和nums2的k/2-1位置大小
if nums1[idx1] < nums2[idx2] {
// 更新nums1
nums1 = nums1[idx1+1:]
// 更新k
k -= idx1 + 1
} else {
// 更新nums2
nums2 = nums2[idx2+1:]
// 更新k
k -= idx2 + 1
}
}
}
|
- 时间复杂度:$O(log(m+n))$
- 空间复杂度:$O(1)$
思路二:划分数组(时间复杂度更低)
在统计中,中位数被用来作为:将一个集合划分为两个长度相等的子集,其中一个子集中的元素总是大于另一个子集中的元素。
首先,在任意位置 i 将 A 划分成两个部分,在任意位置 j 将 B 划分成两个部分:
1
2
3
|
left_part | right_part
A[0], A[1], ..., A[i-1] | A[i], A[i+1], ..., A[m-1]
B[0], B[1], ..., B[j-1] | B[j], B[j+1], ..., B[n-1]
|
当 A 和 B 的总长度是偶数时,如果可以确认:
- $len(left_part)=len(right_part)$
- $max(left_part)≤min(right_part)$
那么,{A,B}中的所有元素就被划分为相同长度的两个部分,且前一部分中的元素总是小于等于后一部分中的元素。中位数就是前一部分的最大值和后一部分的最小值的平均值:
$$median=\frac{max(left_part)+min(right_part)}2$$
当 A 和 B 的总长度是奇数时,如果可以确认:
- $len(left_part)=len(right_part)+1$
- $max(left_part)≤min(right_part)$
那么,{A,B} 中的所有元素已经被划分为两个部分,前一部分比后一部分多一个元素,且前一部分中的元素总是小于或等于后一部分中的元素。中位数就是前一部分的最大值:
$$median=max(left_part)$$
第一个条件对于总长度是偶数和奇数的情况有所不同,但是可以将两种情况合并。第二个条件对于总长度是偶数和奇数的情况是一样的。
要确保这两个条件,只需要保证:
- $i+j=m−i+n−j$(当 m+n 为偶数)或 $i+j=m−i+n−j+1$(当 m+n 为奇数)。等号左侧为前一部分的元素个数,等号右侧为后一部分的元素个数。将 i 和 j 全部移到等号左侧,就可以得到 $i+j=\frac{m+n+1}{2}$,这里的分数结果只保留整数部分(合并条件一)
- $0≤i≤m,0≤j≤n$。规定 A 的长度小于等于 B 的长度,即 $m≤n$。这样对于任意的 $i∈[0,m]$,都有$j=\frac{m+n+1}{2}−i$,$ j∈[0,n]$,那么在 $[0,m]$ 的范围内枚举 i 并得到 j,就不需要额外的性质了
- 如果 A 的长度较大,那么交换 A 和 B 即可
- 如果 $m>n$ ,那么得出的
j 有可能是负数
- $B[j−1]≤A[i]$ 以及 $A[i−1]≤B[j]$,即前一部分的最大值小于等于后一部分的最小值($A[i−1]≤A[i]$ 以及 $B[j−1]≤B[j]$ 是显而易见的)
为了简化分析,假设 $A[i−1],B[j−1],A[i],B[j]$ 总是存在。对于 $i=0、i=m、j=0、j=n$ 这样的临界条件,只需要规定 $A[−1]=B[−1]=−∞,A[m]=B[n]=∞$ 即可。这也是比较直观的:当一个数组不出现在前一部分时,对应的值为负无穷,就不会对前一部分的最大值产生影响;当一个数组不出现在后一部分时,对应的值为正无穷,就不会对后一部分的最小值产生影响
所以需要做的是:
在 $[0,m]$ 中找到 i,使得:
$B[j−1]≤A[i] 且 A[i−1]≤B[j],其中 j=\frac{m+n+1}{2}−i$
⭐可以证明它等价于:
在 $[0,m]$ 中找到最大的 i,使得:
$A[i−1]≤B[j],其中 j=\frac{m+n+1}{2}−i$
证明:
- 当
i 从 0∼m 递增时,A[i−1] 递增,B[j] 递减,所以一定存在一个最大的 i 满足 $A[i−1]≤B[j]$;
- 如果
i 是最大的,那么说明 i+1 不满足上面的不等式。将 i+1 带入可以得到 $A[i]>B[j−1]$,也就是 $B[j−1]<A[i]$,就和进行等价变换前 i 的性质一致了(甚至还要更强)
因此,可以对 i 在 [0,m] 的区间上进行二分搜索,找到满足 $A[i−1]≤B[j]$ 的最大 i 值,就得到了划分的方法。此时,划分前一部分元素中的最大值,以及划分后一部分元素中的最小值,才可能作为就是这两个数组的中位数。
注意:因为要在[0, len(nums1)]上找满足 $A[i−1]≤B[j]$ 的最大i值,所以初始化二分右边界为len(nums1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
|
func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {
// 判nums1长度是否大于nums2
if len(nums1) > len(nums2) {
// 交换nums1和nums2
return findMedianSortedArrays(nums2, nums1)
}
// 初始化划分前一部分的最大值和划分后一部分的最小值
mid1, mid2 := 0, 0
// 初始化双指针指向nums1首尾
left, right := 0, len(nums1)
// 在nums1中找满足nums1[i-1] ≤ nums2[j]的最大i
for left <= right {
// i为中点 j由i计算得到
i := left + (right-left)>>1
j := (len(nums1)+len(nums2)+1)/2 - i
// 求A[i−1],A[i],B[j−1],B[j]
// 对于 i=0、i=m、j=0、j=n 临界条件
// 规定 A[−1]=B[−1]=−∞,A[m]=B[n]=∞
nums1_im1 := math.MinInt
if i != 0 {
nums1_im1 = nums1[i-1]
}
nums1_i := math.MaxInt
if i != len(nums1) {
nums1_i = nums1[i]
}
nums2_jm1 := math.MinInt
if j > 0 {
nums2_jm1 = nums2[j-1]
}
nums2_j := math.MaxInt
if j != len(nums2) {
nums2_j = nums2[j]
}
// 判nums1[i-1]是否小于等于nums2[j]
if nums1_im1 <= nums2_j {
// 保存划分前一部分的最大值
mid1 = max(nums1_im1, nums2_jm1)
// 保存划分后一部分的最小值
mid2 = min(nums1_i, nums2_j)
// 更新左边界找可能的更大i
left = i + 1
} else {
// 更新右边界缩小i尝试满足不等式
right = i - 1
}
}
// 判断总长度是否为偶数
if (len(nums1)+len(nums2))%2 == 0 {
// 返回前一部分最大值和后一部分最小值的平均值
return float64(mid1+mid2) / 2.0
}
// 总长度为奇数直接返回前一部分的最大值
return float64(mid1)
}
// 写法二
func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {
if len(nums1) > len(nums2) {
return findMedianSortedArrays(nums2, nums1)
}
mid1, mid2 := 0, 0
left, right := 0, len(nums1)
for left <= right {
i := left + (right-left)>>1
j := (len(nums1)+len(nums2)+1)/2 - i
nums1_i_1 := math.MinInt
nums2_j_1 := math.MinInt
nums1_i := math.MaxInt
nums2_j := math.MaxInt
if i != 0 {
nums1_i_1 = nums1[i-1]
}
if i != len(nums1) {
nums1_i = nums1[i]
}
if j != 0 {
nums2_j_1 = nums2[j-1]
}
if j != len(nums2) {
nums2_j = nums2[j]
}
if nums1_i_1 <= nums2_j {
mid1 = max(nums1_i_1, nums2_j_1)
mid2 = min(nums1_i, nums2_j)
left = i + 1
} else {
right = i - 1
}
}
if (len(nums1)+len(nums2))%2 != 0 {
return float64(mid1)
}
return float64(mid1+mid2) / 2.0
}
|
- 时间复杂度:$O(logmin(m,n)))$
- 空间复杂度:$O(1)$
多数元素
169. 多数元素 - 力扣(LeetCode)
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。数组是非空的,并且给定的数组总是存在多数元素。**进阶:**尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题
思路:找众数——Boyer-Moore 算法
-
维护一个候选众数 candidate 和它出现的次数 count。初始时 candidate 可以为任意值,count 为 0;
-
遍历数组 nums 中的所有元素,对于每个元素 x,在判断 x 之前,如果 count 的值为 0,先将 x 的值赋予 candidate,随后判断 x:
-
在遍历完成后,candidate 即为整个数组的众数
例如下面的这个数组:
$$[7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]$$
在遍历到数组中的第一个元素以及每个在 | 之后的元素时,candidate 都会因为 count 的值变为 0 而发生改变。最后一次 candidate 的值从 5 变为 7,也就是这个数组中的众数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
func majorityElement(nums []int) int {
candidate, count := 0, 0
for _, v := range nums {
if count == 0 {
candidate = v
}
if v == candidate {
count++
} else {
count--
}
}
return candidate
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
寻找重复数
287. 寻找重复数 - 力扣(LeetCode)
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间
将 nums 数组看作链表,将数组下标 i 和数 nums[i] 建立一个映射关系 i→nums[i],从下标为 0 出发,根据映射关系计算出一个值,以这个值为新的下标,再用这个映射关系计算,以此类推,直到下标超界,这样可以产生一个类似链表一样的序列。由于存在的重复的数字 target,因此 target 这个位置一定有起码两条指向它的边,因此整张图一定存在环,要找到的 target 就是这个环的入口,那么整个问题就等价于 142. 环形链表 II。
设置慢指针 slow 和快指针 fast ,慢指针每次走一步,快指针每次走两步,根据「Floyd 判圈算法」两个指针在有环的情况下一定会相遇,此时再将 slow 放置起点 0,两个指针每次同时移动一步,相遇的点就是答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
func findDuplicate(nums []int) int {
// 初始化为0
slow, fast := 0, 0
// 找相遇点(每次slow前进一步 fast前进两步)
for slow, fast = nums[slow], nums[nums[fast]]; slow != fast; slow, fast = nums[slow], nums[nums[fast]]{}
// slow回首
slow = 0
//
for slow != fast {
// 每次slow和fast都前进一步
slow = nums[slow]
fast = nums[fast]
}
return slow
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
会议室II
253. 会议室 II - 力扣(LeetCode)
LeetCode 253M 会议室 II (Meeting Rooms II) - 知乎 (zhihu.com)
给定一个二维数组,每个一维数组表示一场会议的开始和结束时间,返回所需会议室的最少数量
任务调度器
621. 任务调度器 - 力扣(LeetCode)
给定一个字符数组和整数n,数组元素表示要执行的任务,两个相同任务之间必须有长度为n的冷却时间。任务可以按任意顺序完成,返回完成所有任务所需最短时间
思路:桶思想
建立大小为n+1的桶子,个数为任务数量最多的那个任务,比如下图,等待时间 n=2,A 任务个数 6 个,就建立 6 桶子,每个容量为 3,把一个桶子看作一轮任务

- 先从最简单的情况看起,现在没有其他任务,只完成任务 A 所需的时间应该是
(6-1)*3+1=16,因为最后一个桶子,不存在等待时间。

- 接下来添加其他任务
可以看到 C 其实并没有对总体时间产生影响,因为它被安排在了其他任务的冷却期间;而 B 和 A 数量相同,这会导致需要在最后一个桶子中多执行一次 B 任务,现在需要的时间是(6-1)*3+2=17
前面两种情况,总结起来:总排队时间 = (桶个数 - 1) * (n + 1) + 最后一桶的任务数
- 当冷却时间短,任务种类很多时

比如上图,刚好排满了任务,此时所需时间还是 17,如果现在还要执行两次任务 F,该怎么安排呢?
此时可以临时扩充某些桶子的大小,插进任务 F,对比一下插入前后的任务执行情况:
插入前:ABC | ABC | ABD | ABD | ABD | AB
插入后:ABCF | ABCF | ABD | ABD | ABD | AB
在第一个、第二个桶子里插入了任务F,不难发现无论再继续插入多少任务,都可以类似处理,而且新插入元素肯定满足冷却要求
继续思考一下,这种情况下其实每个任务之间都不存在空余时间,冷却时间已经被完全填满了。也就是说,执行任务所需的时间,就是任务的数量
综上,只需要算两个数:
记录最大任务数量 N,看一下任务数量并列最多的任务有多少个,即最后一个桶子的任务数 X,计算 NUM1=(N-1)*(n+1)+x再计算 NUM2=tasks.size(),返回其中较大值即可
因为存在空闲时间时,说明有空闲块:这时NUM2是不满足整个调度算法的要求的,所以只能取NUM1,此时的NUM1肯定比NUM2大;不存在空闲时间时,说明没有空闲块:这时候NUM1可能会出现不满足调度算法的要求的答案,比如:["A", "A", "A", "B", "B", "C", 'C', 'D'],此时的NUM1是7,明显不满足要求。所以此时只能取较大的数NUM2=8
总结:存在空闲时间时肯定是 NUM1 大,不存在空闲时间时肯定是 NUM2 >= NUM1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
func leastInterval(tasks []byte, n int) int {
// 遍历任务列表统计各任务数量
cnt := [26]int{}
for _, ch := range tasks {
cnt[ch-'A']++
}
maxF, count := 0, 0
// 遍历字符表找最多任务的数量及其任务数
for _, f := range cnt {
if f > maxF {
maxF, count = f, 1
} else if f == maxF {
count++
}
}
// 计算有空余时间的时间间隔
num1 := (maxF-1)*(n+1) + count
// 返回有/无空余时间中的最大值
return max(num1, len(tasks))
}
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
最短无序连续子数组
581. 最短无序连续子数组 - 力扣(LeetCode)
给定一个乱序数组,找出一个最短子数组,将该子数组重排,整个数组会升序,返回该子数组长度
思路一:双指针+排序
拷贝一个给定数组,将其重排后,与原数组比较,找出左右第一个不同的元素即为所求区间
注意:将右边界初始化为-1,可以避免给定数组已有序的情况下,没找到不同,所有没更新l和r,导致最终结果返回-1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
func findUnsortedSubarray(nums []int) int {
// 复制一份原数组重排
temp := make([]int, len(nums))
copy(temp, nums)
sort.Ints(temp)
// 找重排数组与原数组左右第一个不同的元素
left, right := 0, -1
for i := range nums {
if nums[i] != temp[i] {
left = i
break
}
}
for j := len(nums) - 1; j >= 0; j-- {
if nums[j] != temp[j] {
right = j
break
}
}
return right - left + 1
}
|
- 时间复杂度:O(nlogn)
- 空间复杂度:O(n)
思路二:双指针+线性探测
假设把这个数组分成三段,左段 和 右段 是标准的升序数组,中段 数组虽是无序的,但满足最小值大于 左段 的最大值,最大值小于 右段 的最小值
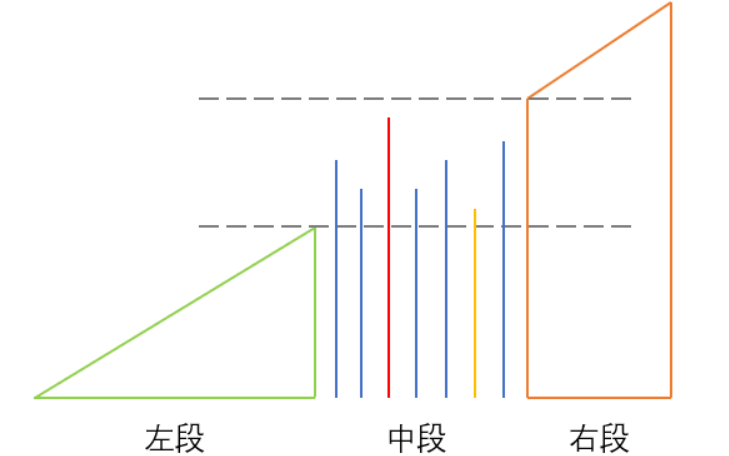
找中段的左右边界,分别定义为L和R,分两头开始遍历:
再遍历到右段之前,会不断更新max和记录的R;当遍历到右段后,由于右段是升序,所以不会再出现比当前max小的,记录的R不会再更新,就是右段第一个元素的前一个元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
func findUnsortedSubarray(nums []int) int {
// 初始化
l, r := 0, -1
max, min := nums[0], nums[len(nums)-1]
// 从左向右遍历找L
for i, v := range nums {
if v < max {
r = i
} else {
max = v
}
}
// 从右向左遍历找R
for i := len(nums)-1; i >= 0; i-- {
if nums[i] > min {
l = i
} else {
min = nums[i]
}
}
return r - l + 1
}
|
删除有序数组中的重复项 II
80. 删除有序数组中的重复项 II - 力扣(LeetCode)
给定一个数组,原地删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。不能使用额外的数组空间,必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成
思路:快慢指针
其中慢指针表示处理出的数组的长度,快指针表示已经检查过的数组的长度;快指针遍历数组,若当前元素与当前处理出的倒数第二个元素不同,则保留到慢指针处,慢指针向右前进一个单位
1
2
3
4
5
6
7
8
9
10
11
12
13
|
func removeDuplicates(nums []int) int {
if len(nums) <= 2 {
return len(nums)
}
slow := 2
for fast := 2; fast < len(nums); fast++ {
if nums[fast] != nums[slow-2] {
nums[slow] = nums[fast]
slow++
}
}
return slow
}
|
H 指数
274. H 指数 - 力扣(LeetCode)
给定一个数组,每个元素代表一篇论文,值代表该论文的引用数,要求返回h指数。h指数是指至少发表了 h 篇论文,并且 至少 有 h 篇论文被引用次数大于等于 h 。如果 h 有多种可能的值,h 指数 是其中最大的那个。
即,给一个数组,求一个最大的 h,使得数组中有至少 h 个数都大于等于 h。
思路:设 n 为 citations 的长度,即这名研究者发表的论文数。根据题意,h 不可能超过 n,所以对于引用次数大于 n 的论文,在统计的时候,可以看成是引用次数等于 n 的论文。例如 n=5,假设 h 是 5,那么无论引用次数是 6 还是 5,都满足 ≥5,所以 6 可以看成是 5,毕竟只需要统计有多少个数字是 ≥5 的。
所以,创建一个长为 n+1 的 cnt 数组,统计 min(citations[i], n) 的出现次数
设 s 为引用次数 ≥i 的论文数,需要算出满足 s ≥ i 的最大的 i
为了快速算出有多少论文的引用次数 ≥ i,我们可以从 i=n 开始倒序循环,每次循环,把 cnt[i] 加到 s 中。由于我们是倒序循环的,只要 s ≥ i 成立,此时的 i 就是满足 s ≥ i 的最大的 i,直接返回 i 作为答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
func hIndex(citations []int) int {
// 统计各引用次数的文章数
cnt := make([]int, len(citations)+1)
for _, v := range citations {
// 引用次数大于总文章数的按总文章数计
cnt[min(v, len(citations))]++
}
// 统计引用次数>=i的文章数
s := 0
// 倒序遍历引用次数
for i := len(citations); i >= 0; i-- {
s += cnt[i]
// 判该大于等于该引用数的文章数是否大于该引用数
// 说明至少有i篇论文的引用次数至少为i
if s >= i {
// 直接返回该引用数
return i
}
}
return 0
}
|
O(1) 时间插入、删除和获取随机元素
380. O(1) 时间插入、删除和获取随机元素 - 力扣(LeetCode)
实现一个类,类中三个方法:插入、删除、随机取一个元素
- 插入:元素若不存在则插入
- 删除:元素若存在则删除
- 随机取:每个元素有相同的概率被返回
思路:哈希表+动态数组
对于 insert 和 remove 操作容易想到使用「哈希表」来实现 O(1) 复杂度,但对于 getRandom 操作,比较理想的情况是能够在一个数组内随机下标进行返回。
将两者结合,可以将哈希表设计为:以入参 val 为键,数组下标 loc 为值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
type RandomizedSet struct {
// k: val v: val在nums中的下标
mp map[int]int
nums []int
}
func Constructor() RandomizedSet {
return RandomizedSet{map[int]int{}, []int{}}
}
func (this *RandomizedSet) Insert(val int) bool {
// 判集合是否存在val
if _, ok := this.mp[val]; !ok {
this.nums = append(this.nums, val)
this.mp[val] = len(this.nums) - 1
return true
}
return false
}
func (this *RandomizedSet) Remove(val int) bool {
// 判集合是否存在val
if _, ok := this.mp[val]; ok {
// 记录要删除元素在数组的下标后
temp := this.mp[val]
// 在数组中删除该元素(用末尾元素覆盖删除元素)
this.nums[temp] = this.nums[len(this.nums)-1]
// 更新末尾元素在字典存储的下标
this.mp[this.nums[temp]] = temp
// 删除末尾元素
this.nums = this.nums[:len(this.nums)-1]
// 在字典中删除
delete(this.mp, val)
return true
}
return false
}
func (this *RandomizedSet) GetRandom() int {
// rand.Seed(time.Now().UnixNano())
randIdx := rand.Intn(len(this.nums))
return this.nums[randIdx]
}
|
罗马数字转整数
13. 罗马数字转整数 - 力扣(LeetCode)
给定每个罗马字符对应的数值,说明了有六种特殊情况,小数在大数紧挨前面,俩字符整体表示为大数-小数;返回给定罗马字符串对应的数值
思路:罗马字符对应数值用哈希表存起来;特殊情况取小数的相反数即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
func romanToInt(s string) int {
mp := map[byte]int{
'I': 1,
'V': 5,
'X': 10,
'L': 50,
'C': 100,
'D': 500,
'M': 1000,
}
res := 0
// 从第二个元素遍历字符
for i := 1; i < len(s); i++ {
// 判当前元素是否大于前一元素
if mp[s[i]] > mp[s[i-1]] {
// 特殊情况:前一元素值取负
res -= mp[s[i-1]]
} else {
res += mp[s[i-1]]
}
}
// 加上最后一个元素
return res + mp[s[len(s)-1]]
}
|
整数转罗马数字
12. 整数转罗马数字 - 力扣(LeetCode)
给定一个整数,返回其罗马数字形式
思路:硬编码
罗马数字由 7 个不同的单字母符号组成,每个符号对应一个具体的数值。此外,减法规则(如问题描述中所述)给出了额外的 6 个复合符号。给了总共 13 个独特的符号(每个符号由 1 个或 2 个字母组成)
用这 13 个符号可以计算出每个数字在每个位上的表示形式,根据 num 每个位上的数字,在硬编码表中查找对应的罗马字符,并将结果拼接在一起,即为 num 对应的罗马数字
1
2
3
4
5
6
7
8
|
var thousands = []string{"", "M", "MM", "MMM"}
var hundreds = []string{"", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM"}
var tens = []string{"", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC"}
var ones = []string{"", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX"}
func intToRoman(num int) string {
return thousands[num/1000] + hundreds[num%1000/100] + tens[num%100/10] + ones[num%10]
}
|
汇总区间
228. 汇总区间 - 力扣(LeetCode)
给定一个 无重复元素 的 有序 整数数组 nums 。返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。也就是说,nums 的每个元素都恰好被某个区间范围所覆盖,并且不存在属于某个范围但不属于 nums 的数字 x 。
列表中的每个区间范围 [a,b] 应该按如下格式输出:
"a->b" ,如果 a != b"a" ,如果 a == b
思路:遍历
从数组的位置 0 出发,向右遍历。每次遇到相邻元素之间的差值大于 1 时,就找到了一个区间。遍历完数组之后,就能得到一系列的区间的列表。
注意:
- 处理数组长度为1的情况
- 处理最后的区间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
func summaryRanges(nums []int) []string {
if len(nums) == 1 {
return []string{strconv.Itoa(nums[0])}
}
res := []string{}
left := 0
for right := 1; right < len(nums); right++ {
// 判当前数字是否与前一数字不连续
if nums[right] != nums[right-1]+1 {
temp := ""
if left == right-1 {
temp = strconv.Itoa(nums[left])
} else {
temp = strconv.Itoa(nums[left]) + "->" + strconv.Itoa(nums[right-1])
}
res = append(res, temp)
left = right
}
// 判当前数字是否是最后一个数字
if right == len(nums)-1 {
temp := ""
if left == right {
temp = strconv.Itoa(nums[left])
} else {
temp = strconv.Itoa(nums[left]) + "->" + strconv.Itoa(nums[right])
}
res = append(res, temp)
left = right
}
}
return res
}
|
插入区间
57. 插入区间 - 力扣(LeetCode)
给定一个 无重叠的 *,*按照区间起始端点排序的区间列表 intervals,其中 intervals[i] = [starti, endi] 表示第 i 个区间的开始和结束,并且 intervals 按照 starti 升序排列。同样给定一个区间 newInterval = [start, end] 表示另一个区间的开始和结束。在 intervals 中插入区间 newInterval,使得 intervals 依然按照 starti 升序排列,且区间之间不重叠(如果有必要的话,可以合并区间)。返回插入之后的 intervals。不需要原地修改 intervals。可以创建一个新数组然后返回它
思路一:暴力
追加、重排、去重叠
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
func insert(intervals [][]int, newInterval []int) [][]int {
// 将新区间追加
intervals = append(intervals, newInterval)
// 升序重排
sort.Slice(intervals, func(i, j int) bool {
return intervals[i][0] < intervals[j][0]
})
res := [][]int{}
// 去重叠
for i := 1; i < len(intervals); i++ {
// 判当前区间是否与前一区间重叠
if intervals[i][0] <= intervals[i-1][1] {
// 更新当前区间
intervals[i][0] = intervals[i-1][0]
intervals[i][1] = max(intervals[i][1], intervals[i-1][1])
// 继续判是否重叠
continue
}
// 收集结果
res = append(res, intervals[i-1])
}
// 收集最后一个区间
res = append(res, intervals[len(intervals)-1])
return res
}
|
思路二:模拟,一次遍历
用指针去扫 intervals,最多可能有三个阶段:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
func insert(intervals [][]int, newInterval []int) [][]int {
res := [][]int{}
// 将新区间之前不重叠的直接加入结果集
i := 0
for ; i < len(intervals); i++ {
// 判当前区间与新区间是否重叠
if intervals[i][1] >= newInterval[0] {
// 重叠则结束循环
break
}
// 不重叠则收集结果
res = append(res, intervals[i])
} // 此时i指向与新区间重叠的第一个区间
// 不断更新新区间
for ; i < len(intervals); i++ {
// 判当前区间与新区间是否不重叠
if intervals[i][0] > newInterval[1] {
// 不重叠则结束循环
break
}
// 更新新区间
newInterval[0] = min(newInterval[0], intervals[i][0])
newInterval[1] = max(newInterval[1], intervals[i][1])
} // 此时i指向不与新区间重叠的第一个区间
// 收集结果(不断更新后的新区间)
res = append(res, newInterval)
// 后面与新区间不重叠的区间直接加入结果
for ; i < len(intervals); i++ {
res = append(res, intervals[i])
}
return res
}
|
寻找峰值
162. 寻找峰值 - 力扣(LeetCode)
给定一个数组,返回其元素的峰值。峰值是指其值严格大于左右相邻值的元素。时间复杂度为 O(log n)
思路:二分查找
若 num[mid] > nums[mid+1],则 num[mid] 可能为峰值,而 nums[mid+1] 必然不为峰值,于是让 right = mid,向左半部分继续找峰值。反之让left = mid+1,向右半部分继续找峰值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
// 写法一
func findPeakElement(nums []int) int {
left, right := 0, len(nums)-1
for left < right {
mid := left + (right-left)/2
if nums[mid] > nums[mid+1] {
right = mid
} else {
left = mid + 1
}
}
return left
}
// 写法二
func findPeakElement(nums []int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right-left)>>1
if mid != 0 && nums[mid] < nums[mid-1] {
right = mid - 1
} else if mid != len(nums)-1 && nums[mid] < nums[mid+1] {
left = mid + 1
} else {
return mid
}
}
return -1
}
|
数组中的第K个最大元素
215. 数组中的第K个最大元素 - 力扣(LeetCode)
给定一个数组,返回第k大的元素
思路一:快排
三路划分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
func findKthLargest(nums []int, k int) int {
rand.Seed(time.Now().UnixNano())
randIdx := rand.Intn(len(nums))
// 初始基准值为首元素
pivot := nums[randIdx]
// 记录比基准值大\等\小的全部元素
big, equal, small := make([]int, 0), make([]int, 0), make([]int, 0)
// 遍历数组划分三种元素
for _, v := range nums {
if v > pivot {
big = append(big, v)
} else if v < pivot {
small = append(small, v)
} else {
equal = append(equal, v)
}
}
if k <= len(big) {
// k一定在big中
return findKthLargest(big, k)
} else if k > len(big)+len(equal) {
// k一定在small中
return findKthLargest(small, k-len(big)-len(equal))
} else {
// k一定在equal中
return pivot
}
}
|
- 时间复杂度:O(n)
- 空间复杂度:O(logn),划分函数的平均递归深度
思路二:大顶堆
全部元素构成一个大顶堆,堆排序时返回第k大元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
func findKthLargest(nums []int, k int) int {
// 1.构建大顶堆
// 从尾节点的父节点向上构建
for i := len(nums)/2 - 1; i >= 0; i-- {
heapify(nums, len(nums), i)
}
// 2.堆排序得到第k大元素
// 从尾节点开始交换堆顶
for i := len(nums) - 1; i >= 0; i-- {
if k == 1 {
return nums[0]
}
k--
nums[0], nums[i] = nums[i], nums[0]
heapify(nums, i, 0)
}
return nums[0]
}
// 向下堆化根为cur的nums[0, length-1]堆
func heapify(nums []int, length, cur int) {
largest := cur
left := 2*cur + 1
right := 2*cur + 2
// 判左孩子是否大于根
if left < length && nums[left] > nums[largest] {
// 标记最大根
largest = left
}
// 判右孩子是否大于根或右节点
if right < length && nums[right] > nums[largest] {
largest = right
}
// 判左孩子是否大于当前节点
if largest != cur {
nums[cur], nums[largest] = nums[largest], nums[cur]
heapify(nums, length, largest)
}
}
|
- 时间复杂度:O(nlogn),建堆的时间代价是 O(n),堆排序的总代价是O(klogn)
- 时间复杂度:O(logn),递归使用栈空间的空间代价
思路三:小顶堆
求第k大,也就是求数组升序重排后后面k个元素中最小的,因此维护一个大小为k的小顶堆,保存最大的k个元素,遍历完数组返回堆顶即可
- 初始化一个大小为k的小顶堆
- 遍历剩余元素,若小于堆顶,则跳过;若大于堆顶,则直接替换掉堆顶,从堆顶重新堆化
- 返回堆顶
拓展:求第k小,也就是求数组升序重排后前面k个元素中最大的,因此维护一个大小为k的大顶堆,保存最小的k个元素,遍历完数组返回堆顶即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
func findKthLargest(nums []int, k int) int {
// 1.维护大小为k的小顶堆(保存nums中最大的k个元素,堆顶是k个最大元素中最小的)
heap := make([]int, k)
// 2.将前k个元素加入小顶堆
for i := 0; i < k; i++ {
heap[i] = nums[i]
}
// 3.堆化:从尾节点的父节点向上遍历到根
for i := len(heap)/2 - 1; i >= 0; i-- {
heapify(heap, i)
}
// 4.遍历剩余元素
for i := k; i < len(nums); i++ {
// 判当前元素是否大于堆顶
if nums[i] > heap[0] {
// 替换掉堆顶
heap[0] = nums[i]
// 从堆顶重新堆化
heapify(heap, 0)
}
}
// 返回堆顶
return heap[0]
}
// 堆化根为cur的小顶堆
func heapify(nums []int, cur int) {
smallest := cur
left := 2*cur + 1
right := 2*cur + 2
// 判左孩子是否小于根
if left < len(nums) && nums[left] < nums[smallest] {
smallest = left
}
// 判右孩子是否小于根或右节点
if right < len(nums) && nums[right] < nums[smallest] {
smallest = right
}
if smallest != cur {
nums[cur], nums[smallest] = nums[smallest], nums[cur]
heapify(nums, smallest)
}
}
|
- 时间复杂度:O(n),建堆的时间代价是 O(k),遍历数组O(n),堆内元素调整O(klogk)=O(1)
- 空间复杂度:O(k)
查找和最小的 K 对数字
373. 查找和最小的 K 对数字 - 力扣(LeetCode)
给定两个升序数组 nums1 和 nums2 , 以及一个整数 k 。定义一对值 (u,v),其中第一个元素来自 nums1,第二个元素来自 nums2 。找到和最小的 k 个数对 (u1,v1), (u2,v2) … (uk,vk) 返回
思路:小顶堆
假设i,j最小——>可能的次小i,j+1、i+1,j入堆——>有数对重复入堆——>规定只入堆i,j+1——>初始入堆0,0后i一直为0不变——>初始入堆各个i,0
为描述方便,下文把nums1记作a,nums2记作b。
由于数组是有序的,(a[0],b[0])是和最小的数对,计入答案。次小的只能是 (a[0],b[1]) 或 (a[1],b[0])。
为了更高效地比大小,借助最小堆来优化:堆中保存下标(i, j),堆顶是最小的 a[i]+b[j]。初始把 (0,0) 入堆。每次出堆时,可能成为次小数对的(i+1,j) 和 (i,j+1)入堆。
但这会导致一个问题:例如当 (1,0) 出堆时,会把 (1,1) 入堆;当 (0,1) 出堆时,也会把 (1,1) 入堆,这样堆中会有重复元素。为了避免有重复元素,规定 (i,j−1) 出堆时,将 (i,j) 入堆;而 (i−1,j) 出堆时只计入答案,其它什么也不做。
换句话说,在 (i,j) 出堆时,只需将 (i,j+1) 入堆,无需将 (i+1,j) 入堆。
但若按照该规则,初始仅把 (0,0) 入堆的话,只会得到 (0,1),(0,2),⋯这些下标对。
所以初始不仅要把 (0,0) 入堆,(1,0),(2,0),⋯ (min(k, n), 0) 这些都要入堆。
注意:
- 堆的初始长度设为
min(k, n),保证当k<n时,只初始化k个数对,当n<k时,只能初始化n个数对
- 代码实现时,为了方便比较大小,实际入堆的是三元组
(i, j, a[i]+b[j])
- 也可以在循环的过程中去把
(i+1,0) 入堆。由于一开始堆的大小不大,出堆入堆更快,整体效率更高。
写法一:自实现小顶堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
|
type Heap [][]int
func kSmallestPairs(nums1 []int, nums2 []int, k int) [][]int {
// 初始化一个大小为min(k, n)的小顶堆
heap := make(Heap, min(k, len(nums1)))
// 初始化加入(0,0,v)(1,0,v)...(min(k, n),0,v)
for i := range heap {
heap[i] = []int{i, 0, nums1[i] + nums2[0]}
}
// 维护小顶堆(取堆顶最小->可能的次小入堆)k次
res := [][]int{}
for cnt := 0; cnt < k; cnt++ {
// 取堆顶(i, j)
i, j := heap[0][0], heap[0][1]
// (a[i], b[j])加入结果集
res = append(res, []int{nums1[i], nums2[j]})
heap.Pop()
// 加入(i, j+1)
// 防止越界
if j+1 < len(nums2) {
heap.Push(i, j+1, nums1[i]+nums2[j+1])
}
}
return res
}
func (h Heap) swap(i, j int) {
h[i], h[j] = h[j], h[i]
}
func (h Heap) less(i, j int) bool {
return h[i][2] < h[j][2]
}
func (h Heap) up(i int) {
father := (i - 1) / 2
if father >= 0 && h.less(i, father) {
h.swap(father, i)
h.up(father)
}
}
func (h Heap) down(i int) {
largest := i
left := 2*i + 1
right := 2*i + 2
if left < len(h) && h.less(left, largest) {
largest = left
}
if right < len(h) && h.less(right, largest) {
largest = right
}
if largest != i {
h.swap(largest, i)
h.down(largest)
}
}
func (h *Heap) Push(i, j, v int) {
*h = append(*h, []int{i, j, v})
h.up(len(*h) - 1)
}
func (h *Heap) Remove(i int) ([]int, bool) {
if i < 0 || i >= len((*h)) {
return []int{}, false
}
h.swap(i, len(*h)-1)
x := (*h)[len(*h)-1]
*h = (*h)[:len(*h)-1]
if i < len(*h) {
father := (i - 1) / 2
if father >= 0 && h.less(i, father) {
h.up(i)
} else {
h.down(i)
}
}
return x, true
}
func (h *Heap) Pop() []int {
x, _ := h.Remove(0)
return x
}
|
写法二:自实现小顶堆 循环中加入(i+1, 0)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
|
type Heap [][]int
func kSmallestPairs(nums1 []int, nums2 []int, k int) [][]int {
// 初始化小顶堆加入(0,0,v)
heap := Heap{[]int{0, 0, nums1[0] + nums2[0]}}
// 维护小顶堆(取堆顶最小->可能的次小入堆)k次
res := make([][]int, 0, k)
for cnt := 0; cnt < k; cnt++ {
// 取堆顶(i, j)
i, j := heap[0][0], heap[0][1]
// (a[i], b[j])加入结果集
res = append(res, []int{nums1[i], nums2[j]})
heap.Pop()
// 当j=0时,加入(i+1, 0)
if j == 0 && i+1 < len(nums1) {
heap.Push(i+1, 0, nums1[i+1]+nums2[0])
}
// 加入(i, j+1)
// 防止越界
if j+1 < len(nums2) {
heap.Push(i, j+1, nums1[i]+nums2[j+1])
}
}
return res
}
func (h Heap) swap(i, j int) {
h[i], h[j] = h[j], h[i]
}
func (h Heap) less(i, j int) bool {
return h[i][2] < h[j][2]
}
func (h Heap) up(i int) {
father := (i - 1) / 2
if father >= 0 && h.less(i, father) {
h.swap(father, i)
h.up(father)
}
}
func (h Heap) down(i int) {
largest := i
left := 2*i + 1
right := 2*i + 2
if left < len(h) && h.less(left, largest) {
largest = left
}
if right < len(h) && h.less(right, largest) {
largest = right
}
if largest != i {
h.swap(largest, i)
h.down(largest)
}
}
func (h *Heap) Push(i, j, v int) {
*h = append(*h, []int{i, j, v})
h.up(len(*h) - 1)
}
func (h *Heap) Remove(i int) ([]int, bool) {
if i < 0 || i >= len((*h)) {
return []int{}, false
}
h.swap(i, len(*h)-1)
x := (*h)[len(*h)-1]
*h = (*h)[:len(*h)-1]
if i < len(*h) {
father := (i - 1) / 2
if father >= 0 && h.less(i, father) {
h.up(i)
} else {
h.down(i)
}
}
return x, true
}
func (h *Heap) Pop() []int {
x, _ := h.Remove(0)
return x
}
|
写法三:标准库
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
func kSmallestPairs(nums1 []int, nums2 []int, k int) [][]int {
// 初始化小顶堆加入(0,0,v)
h := Heap{[]int{0, 0, nums1[0] + nums2[0]}}
// 维护小顶堆(取堆顶最小->可能的次小入堆)k次
res := make([][]int, 0, k)
for cnt := 0; cnt < k; cnt++ {
// 取堆顶(i, j)
p := heap.Pop(&h).([]int)
i, j := p[0], p[1]
// (a[i], b[j])加入结果集
res = append(res, []int{nums1[i], nums2[j]})
// 当j=0时,加入(i+1, 0)
if j == 0 && i+1 < len(nums1) {
heap.Push(&h, []int{i + 1, 0, nums1[i+1] + nums2[0]})
}
// 加入(i, j+1)
// 防止越界
if j+1 < len(nums2) {
heap.Push(&h, []int{i, j + 1, nums1[i] + nums2[j+1]})
}
}
return res
}
type Heap [][]int
func (h Heap) Len() int { return len(h) }
func (h Heap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h Heap) Less(i, j int) bool { return h[i][2] < h[j][2] }
func (h *Heap) Push(v any) { *h = append(*h, v.([]int)) }
func (h *Heap) Pop() any { x := (*h)[len(*h)-1]; *h = (*h)[:len(*h)-1]; return x }
|
- 时间复杂度:O(klogmin(n,k)),其中 n 为 nums1的长度。为了得到 k 个数对,需要循环 k 次,每次出堆入堆的时间复杂度为 logmin(n,k)。所以总的时间复杂度为 O(klogmin(n,k))。
- 空间复杂度:O(min(n,k))。堆中至多有 O(min(n,k)) 个三元组。
回文数
9. 回文数 - 力扣(LeetCode)
给定一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
思路一:将数字转换为字符串,并检查字符串是否为回文。但是,这需要额外的非常量空间。
思路二:将数字本身反转,然后将反转后的数字与原始数字进行比较,但反转后的数字可能溢出。
思路三:只翻转数字的后半部分,将其与前半部分比较。
关键点:如何知道反转数字的位数已经达到原始数字位数的一半?
由于整个过程不断将原始数字除以 10,然后给反转后的数字乘上 10,所以,当原始数字小于或等于反转后的数字时,就意味着已经处理了一半位数的数字了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
func isPalindrome(x int) bool {
// 排除负数和个位为0的非0数
if x < 0 || (x%10 == 0 && x != 0) {
return false
}
// 每次取一位倒序拼接出后半部分x
num := 0
for x > num {
num *= 10
num += x % 10
x /= 10
}
// 偶||奇去尾
return x == num || x == num/10
}
|
- 时间复杂度:O(logn),对于每次迭代,会将输入除以 10,因此时间复杂度为 O(logn)。
- 空间复杂度:O(1)。只需要常数空间存放若干变量
加一
66. 加一 - 力扣(LeetCode)
给定一个由整数非空数组所表示的非负整数,在该数的基础上加一。最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。除了整数 0 之外,这个整数不会以零开头
思路:倒序遍历数组,判当前位加一是否有进位,若有则标记进位,当前位置0,继续向前遍历;若无进位,则当前位加一直接结束遍历。全部元素遍历完后须判断仍有进位
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
func plusOne(digits []int) []int {
ca := false
for i := len(digits) - 1; i >= 0; i-- {
if digits[i]+1 > 9 {
ca = true
digits[i] = 0
} else {
digits[i]++
ca = false
break
}
}
if ca {
res := append([]int{1}, digits...)
return res
}
return digits
}
|
- 时间复杂度:O(n),其中 n 是数组 digits 的长度。
- 空间复杂度:O(n)
阶乘后的零
172. 阶乘后的零 - 力扣(LeetCode)
给定一个整数 n ,返回 n! 结果中尾随零的数量
思路:对于任意一个 n! 而言,其尾随零的个数取决于展开式中 10 的个数,例如10!=3628800=36288×10 2 ,尾零个数为 2。而 10 可由质因数 2×5 而来,故 n! 的尾随零个数为展开式中各项分解质因数后「2 的数量」和「5 的数量」中的较小值。 由于 5 的个数必然不会超过质因数 2 的个数。 因此只需要统计质因数 5 的个数即可
关键点:统计n!中质因数 5 的个数
方法:用n不断除 5 累加商得到的和,即为n!中质因数 5 的个数
1
2
3
4
5
6
7
8
9
|
func trailingZeroes(n int) int {
res := 0
for n > 0 {
n /= 5
// 累加除5的商
res += n
}
return res
}
|
Pow(x, n)
50. Pow(x, n) - 力扣(LeetCode)
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,xn )
思路:将幂次看作二进制数,从低位到高位遍历。在遍历过程中不断对x自身平方,可以得到x->x2->x4->x8。若遇到1说明当前二进制位代表的十进制幂次是一个因数,则将当前二进制位代表的十进制幂次的x乘入结果集。
注意:若幂次为负,x取1/x,n取相反数即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
func myPow(x float64, n int) float64 {
res := 1.0
// 判幂次是否为负数
if n < 0 {
x = 1 / x
n = -n
}
for n > 0 {
// 判幂次n二进制当前位是否为1
if n&1 == 1 {
res *= x
}
// x不断平方
x *= x
// n右移一位
n >>= 1
}
return res
}
|
- 时间复杂度:O(log∣n∣)
- 空间复杂度:O(1)
直线上最多的点数
149. 直线上最多的点数 - 力扣(LeetCode)
给定一个数组 points ,其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上
思路一:枚举直线 + 枚举统计
枚举两点(确定一条线),然后检查其余点是否落在该线中。
为了避免除法精度问题,枚举两个点 a 和 b 时,不直接计算其对应直线的斜率,而是通过判断 a 和 b 与第三个点 c 形成的两条直线斜率是否相等,来得知点 p 是否落在该直线上
kab = ya-yb/xa-xb kbc = yb-yc/xb-xc
(ya-yb) × (xb-xc) = (xa-xb) × (yb-yc)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
func maxPoints(points [][]int) int {
res := 1
for i := 0; i < len(points); i++ {
for j := i + 1; j < len(points); j++ {
// 初始i, j两点
cnt := 2
// 遍历i, j之外的其他点
for k := j + 1; k < len(points); k++ {
// 判Kab是否等于Kbc
if (points[i][1]-points[j][1])*(points[j][0]-points[k][0]) == (points[i][0]-points[j][0])*(points[j][1]-points[k][1]) {
cnt++
}
}
res = max(res, cnt)
}
}
return res
}
|
思路二:枚举直线 + 哈希表统计
枚举所有直线的过程不可避免,但统计点数的过程可以优化。
具体的,先枚举所有可能出现的 直线斜率,使用「哈希表」统计所有 斜率 对应的点的数量,在所有值中取 max 即是答案。
细节:在使用「哈希表」进行保存时,为了避免精度问题,直接使用字符串进行保存,同时需要将 斜率 约干净。
- 先求出分子和分母
- 找出分子分母的最大公因数
- 用分子分母分别除最大公因数,中间指定特殊连接符连接,作为
key存入哈希表
求最大公因数用辗转相除法:两数相除,余数为0时,除数为最大公约数;余数不为0时,除数->被除数,余数->除数,重复进行相除,直到余数为0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
func maxPoints(points [][]int) int {
res := 1
for i := 0; i < len(points); i++ {
mp := map[string]int{}
// 由点 i 发出的直线所经过的最多点数量
for j := i + 1; j < len(points); j++ {
deltaY := points[i][1] - points[j][1]
deltaX := points[i][0] - points[j][0]
g := gcd(deltaY, deltaX)
key := strconv.Itoa(deltaY/g) + "_" + strconv.Itoa(deltaX/g)
mp[key]++
// +1是加上当前点i
res = max(res, mp[key]+1)
}
}
return res
}
func gcd(a, b int) int {
if b == 0 {
return a
}
return gcd(b, a%b)
}
|
- 时间复杂度:枚举所有直线的复杂度为 O(n^2);令坐标值的最大差值为 m,gcd 复杂度为 O(logm)。整体复杂度为 O(n^2×logm)
- 空间复杂度:O(n)
最大连续1的个数 III
1004. 最大连续1的个数 III - 力扣(LeetCode)
给定一个二进制数组 nums 和一个整数 k,假设最多可以将 k 个 0改为1 ,返回执行修改后 数组中连续 1 的最大个数
思路:滑动窗口
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
func longestOnes(nums []int, k int) int {
res := 0
// 滑动窗口
left, right := 0, 0
// 统计窗口内0的个数
cnt := 0
for right < len(nums) {
if nums[right] == 0 {
cnt++
}
// 移动左边界直至窗口内0个数不超标
for cnt > k {
if nums[left] == 0 {
cnt--
}
left++
}
res = max(res, right-left+1)
right++
}
return res
}
|
删掉一个元素以后全为 1 的最长子数组
1493. 删掉一个元素以后全为 1 的最长子数组 - 力扣(LeetCode)
给定一个二进制数组 nums ,需要从中删掉一个元素。返回最长的且只包含 1 的非空子数组的长度。如果不存在这样的子数组,请返回 0
思路:滑动窗口
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
func longestSubarray(nums []int) int {
res := 0
// 滑动窗口
left := 0
// 统计窗口内0个数
cnt := 0
for right := 0; right < len(nums); right++ {
if nums[right] == 0 {
cnt++
}
// 移动左边界直至0的个数不超过1
for cnt > 1 {
if nums[left] == 0 {
cnt--
}
left++
}
res = max(res, right-left)
}
return res
}
|
找到最高海拔
1732. 找到最高海拔 - 力扣(LeetCode)
给一个长度为 n 的整数数组 gain ,其中 gain[i] 是点 i 和点 i + 1 的 净海拔高度差(0 <= i < n)。返回 最高点的海拔
思路:前缀和
1
2
3
4
5
6
7
8
9
|
func largestAltitude(gain []int) int {
res := 0
preSum := 0
for _, v := range gain {
preSum += v
res = max(res, preSum)
}
return res
}
|
拥有最多糖果的孩子
1431. 拥有最多糖果的孩子 - 力扣(LeetCode)
给定一个数组,每个元素表示每个孩子目前手中的糖果数,给定一个整数,表示可分配的糖果数。返回一个长度为 n 的布尔数组 result,如果把所有的 extraCandies 给第 i 个孩子之后,他会拥有所有孩子中 最多 的糖果,那么 result[i] 为 true,否则为 false
思路:先统计出分配前孩子拥有的最多糖果数,再遍历孩子分配糖果,判断是否大于等于最多糖果数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
func kidsWithCandies(candies []int, extraCandies int) []bool {
res := make([]bool, len(candies))
// 统计出孩子拥有的最多糖果数
maxCandies := 0
for _, v := range candies {
maxCandies = max(v, maxCandies)
}
// 遍历孩子分配糖果
for i, v := range candies {
if v+extraCandies >= maxCandies {
res[i] = true
}
}
return res
}
|
种花问题
605. 种花问题 - 力扣(LeetCode)
给定一个整数数组 flowerbed 表示花坛,由若干 0 和 1 组成,其中 0 表示没种植花,1 表示种植了花。另有一个数 n ,能否在不打破种植规则的情况下种入 n 朵花?能则返回 true ,不能则返回 false。种植规则:花不能相邻
思路:遍历模拟
1
2
3
4
5
6
7
8
9
|
func canPlaceFlowers(flowerbed []int, n int) bool {
for i, v := range flowerbed {
if v == 0 && (i == 0 || flowerbed[i-1] == 0) && (i == len(flowerbed)-1 || flowerbed[i+1] == 0) {
flowerbed[i] = 1
n--
}
}
return n <= 0
}
|
K 和数对的最大数目
1679. K 和数对的最大数目 - 力扣(LeetCode)
给定一个整数数组 nums 和一个整数 k 。每一步操作中,需要从数组中选出和为 k 的两个整数,并将它们移出数组。返回可以对数组执行的最大操作数
思路:升序重排+双指针
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
func maxOperations(nums []int, k int) int {
res := 0
sort.Ints(nums)
left, right := 0, len(nums)-1
for left < right {
if nums[left]+nums[right] == k {
res++
left++
right--
} else if nums[left]+nums[right] < k {
left++
} else {
right--
}
}
return res
}
|
子数组最大平均数 I
643. 子数组最大平均数 I - 力扣(LeetCode)
给定一个由 n 个元素组成的整数数组 nums 和一个整数 k 。找出平均数最大且 长度为 k 的连续子数组,并输出该最大平均数
思路:维护一个大小为k的滑动窗口
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
func findMaxAverage(nums []int, k int) float64 {
// 维护大小为k的滑动窗口
left, right := 0, 0
sum, maxSum := 0, 0
for ; right < k; right++ {
sum += nums[right]
}
maxSum = sum
for ; right < len(nums); right++ {
sum -= nums[left]
left++
sum += nums[right]
maxSum = max(maxSum, sum)
}
fmt.Println(maxSum)
return float64(maxSum) / float64(k)
}
|
定长子串中元音的最大数目
1456. 定长子串中元音的最大数目 - 力扣(LeetCode)
给定字符串 s 和整数 k 。返回字符串 s 中长度为 k 的单个子字符串中可能包含的最大元音字母数
思路:维护一个大小为k的滑动窗口
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
func maxVowels(s string, k int) int {
res := 0
// 维护大小为k的滑动窗口
left, right := 0, 0
cnt := 0
for ; right < k; right++ {
if strings.Contains("aeiou", string(s[right])) {
cnt++
}
}
res = cnt
for ; right < len(s); right++ {
if strings.Contains("aeiou", string(s[left])) {
cnt--
}
left++
if strings.Contains("aeiou", string(s[right])) {
cnt++
res = max(res, cnt)
}
}
return res
}
|
猜数字大小
374. 猜数字大小 - 力扣(LeetCode)
从 1 到 n 随机选择一个数字。 猜选出的是哪个数字
思路:二分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
func guessNumber(n int) int {
left := 1
for left <= n {
mid := left + (n-left)>>1
if guess(mid) == 0 {
return mid
} else if guess(mid) == 1 {
left = mid + 1
} else {
n = mid - 1
}
}
return -1
}
|
咒语和药水的成功对数
2300. 咒语和药水的成功对数 - 力扣(LeetCode)
给定两个数组和一个整数success,若nums1[i] * nums2[j] >= success ,则视为一对 成功 的组合。返回nums1长度的整数数组 pairs,其中 pairs[i] 是能跟nums1[i]成功组合的 nums2 数目
思路:重排后二分查找nums2
- 对于每个
nums1,求出target = ⌈success/nums1[i]⌉,即向上取整,(success-1)/spell+1
- 在
nums2中二分查找第一个大于等于target的值
注意:⌈x⌉ 表示不小于 x 的最小整数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
func successfulPairs(spells []int, potions []int, success int64) []int {
res := make([]int, len(spells))
sort.Ints(potions)
for i, spell := range spells {
target := (int(success)-1)/spell + 1
left, right := 0, len(potions)-1
for left <= right {
mid := left + (right-left)/2
if potions[mid] < target {
left = mid + 1
} else {
right = mid - 1
}
}
if left >= 0 && left < len(potions) && potions[left] >= target {
res[i] = len(potions) - left
}
}
return res
}
|
- 时间复杂度:O(m×logm+n×logm),其中 n 为数组 spells 的长度,m 是数组 postion 的长度,主要为对数组 potions 排序和对数组 spells 中每一个元素对数组 potions 进行「二分查找」的时间开销。
- 空间复杂度:O(logm),主要为对 potions 排序的空间开销,其中返回的答案不计入空间复杂度
爱吃香蕉的珂珂
875. 爱吃香蕉的珂珂 - 力扣(LeetCode)
给定一个长度为n的数组表示有n堆香蕉,每个元素是该堆香蕉的个数,给定一个整数为小时数。每小时选一堆香蕉吃,要求返回在 h 小时内吃掉所有香蕉的最小速度 k(k 为整数,单位:根/小时)
思路:二分搜索k
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
func minEatingSpeed(piles []int, h int) int {
isEatAll := func(k int) bool {
spare := 0
for _, pile := range piles {
if pile <= k {
spare += 1
} else if pile%k == 0 {
spare += pile / k
} else {
spare += pile/k + 1
}
}
return spare <= h
}
left, right := 1, slices.Max(piles)
for left <= right {
mid := left + (right-left)>>1
if isEatAll(mid) {
right = mid - 1
} else {
left = mid + 1
}
}
return left
}
|
戳印序列
936. 戳印序列 - 力扣(LeetCode)
要用小写字母组成一个目标字符串 target,开始的时候,序列由 target.length 个 '?' 记号组成。有一个小写字母印章 stamp,在每个回合,将印章放在序列上,并将序列中的每个字母替换为印章上的相应字母。如果可以印出序列,那么返回一个数组,该数组由每个回合中被印下的最左边字母的索引组成。如果不能印出序列,就返回一个空数组。
思路:反推
由于某一个戳印会将前面的戳印覆盖掉,所以正着考虑将问号序列变为目标序列很难下手。而将目标序列 target 变为问号序列,就可解决了
将 target 中从第 i 个字符开始的长度为 stamp.length 的字符串称为第 i 个窗口。在第一步时,只有和 stamp 完全匹配的窗口才能进行戳印,而被戳印的所有位置都会变成问号 ?,在后续的戳印过程中,问号可以匹配任意字符
- 不断循环直至
targetByte全为?或没有位置可以盖印
- 用一个变量记录本次遍历
targetByte是否找到盖章位置
- 遍历
targetByte所有可能位置,若当前位置起始要盖章的位置全为?或有字符不相等且不为?,则说明该位置不能盖章,否则说明该位置可以盖章
- 找到盖章位置后记入结果集,记录本回合找到盖章位置,盖章修改为
?,结束本回合
- 回合结束后判断本回合是否找到盖章位置,若没有则说明无地方可盖,直接结束,判是否全为
?;否则继续下一回合
- 最后判断全为
?,若不是,则返回空数组,否则返回反转后的结果集(反推思路,结果要反转回去)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
|
func movesToStamp(stamp string, target string) []int {
res := []int{}
// 创建全?的最终目标字符串
endTarget := make([]byte, len(target))
for i := range endTarget {
endTarget[i] = '?'
}
// 将target转为字符数组
targetByte := []byte(target)
// 不断循环直至targetByte全为?或没有位置可以盖印
for string(targetByte) != string(endTarget) {
// 标记本次遍历targetByte是否找到盖章位置
isModfied := false
// 遍历targetByte所有可能位置
for i := 0; i <= len(targetByte)-len(stamp); i++ {
// 判当前位置作为起始能否盖章
if func() bool {
// 判当前位置起始要盖章的位置是否不全为?
if func() bool {
for j := 0; j < len(stamp); j++ {
if targetByte[i+j] != '?' {
return true
}
}
return false
}() {
for j := 0; j < len(stamp); j++ {
if targetByte[i+j] != stamp[j] && targetByte[i+j] != '?' {
// 有字符不相等且不为?
return false
}
}
return true
}
return false
}() {
// 保存找到的盖章位置
res = append(res, i)
isModfied = true
// i起始修改为?
for j := 0; j < len(stamp); j++ {
targetByte[i+j] = '?'
}
break
}
}
// 判本次遍历是否找到盖章位置
if !isModfied {
break
}
}
if string(targetByte) != string(endTarget) {
return []int{}
}
// 倒序返回res
slices.Reverse(res)
return res
}
|
合并两个有序数组
88. 合并两个有序数组 - 力扣(LeetCode)
给定两个数组,按升序合并到第一个数组
思路:倒序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
func merge(nums1 []int, m int, nums2 []int, n int) {
idx1, idx2, idx := m-1, n-1, len(nums1)-1
for idx2 >= 0 {
if idx1 >= 0 && nums1[idx1] >= nums2[idx2] {
nums1[idx] = nums1[idx1]
idx1--
} else {
nums1[idx] = nums2[idx2]
idx2--
}
idx--
}
return
}
|
比较版本号
给两个 版本号字符串 version1 和 version2 ,比较它们。版本号由被点 '.' 分开的修订号组成。修订号的值 是它 转换为整数 并忽略前导零。比较版本号时,按 从左到右的顺序 依次比较它们的修订号。如果其中一个版本字符串的修订号较少,则将缺失的修订号视为 0。返回规则如下:
- 如果
*version1* < *version2* 返回 -1,
- 如果
*version1* > *version2* 返回 1,
- 除此之外返回
0
思路:双指针转为整数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
func compareVersion(version1 string, version2 string) int {
idx1, idx2 := 0, 0
for idx1 < len(version1) || idx2 < len(version2) {
x := 0
for ; idx1 < len(version1) && version1[idx1] != '.'; idx1++ {
x = x*10 + int(version1[idx1]-'0')
}
// 跳过.
idx1++
y := 0
for ; idx2 < len(version2) && version2[idx2] != '.'; idx2++ {
y = y*10 + int(version2[idx2]-'0')
}
// 跳过.
idx2++
if x < y {
return -1
}
if x > y {
return 1
}
}
return 0
}
|
重复的DNA序列
187. 重复的DNA序列 - 力扣(LeetCode)
DNA序列 由一系列核苷酸组成,缩写为 'A', 'C', 'G' 和 'T'。例如,"ACGAATTCCG" 是一个 DNA序列 。给定一个表示 DNA序列 的字符串 s ,返回所有在 DNA 分子中出现不止一次的 长度为 10 的序列(子字符串)。可以按 任意顺序 返回答案。
思路:滑动窗口+哈希表+二进制
由于 s 中只含有 4 种字符,所以可以将每个字符用 2 个比特表示,即:A 表示为二进制 00;C 表示为二进制 01;G 表示为二进制 10;T 表示为二进制 11
如此,一个长为 10 的字符串就可以用 20 个比特表示,而一个 int 整数有 32 个比特,足够容纳该字符串,因此可以将 s 的每个长为 10 的子串用一个 int 整数表示
用一个哈希表统计 s 所有长度为 10 的子串的出现次数
为了优化时间复杂度,可以用一个大小固定为 10 的滑动窗口来计算子串的整数表示。设当前滑动窗口对应的整数表示为 x,当计算下一个子串时,就将滑动窗口向右移动一位,此时会有一个新的字符进入窗口,以及窗口最左边的字符离开窗口,这些操作对应的位运算,按计算顺序表示如下:
- 滑动窗口向右移动一位:
x = x << 2,由于每个字符用 2 个比特表示,所以要左移 2 位;
- 一个新的字符 ch 进入窗口:
x = x | bin[ch],这里 bin[ch] 为字符 ch 的对应二进制;
- 窗口最左边的字符离开窗口:
x = x & ((1 << 20) - 1),由于只考虑 x 的低 20 位比特,需要将其余位置零,即 (1 << 20) - 1。
将这三步合并,就可以用 O(1) 的时间计算出下一个子串的整数表示,即 x = ((x << 2) | bin[ch]) & ((1 << 20) - 1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
var bin = map[byte]int{
'A': 0,
'C': 1,
'G': 2,
'T': 3,
}
func findRepeatedDnaSequences(s string) []string {
if len(s) < 10 {
return []string{}
}
res := []string{}
mp := map[int]int{}
x := 0
// 初始化窗口值
for i := 0; i < 9; i++ {
x = x<<2 | bin[byte(s[i])]
}
// 滑动窗口
for right := 9; right < len(s); right++ {
// 先右边字符入窗再左边字符出窗
x = (x<<2 | bin[byte(s[right])]) & (1<<20 - 1)
mp[x]++
if mp[x] == 2 {
res = append(res, s[right-9:right+1])
}
}
return res
}
|
找到 K 个最接近的元素
658. 找到 K 个最接近的元素 - 力扣(LeetCode)
给定一个 排序好 的数组 arr ,两个整数 k 和 x ,从数组中找到最靠近 x(两数之差最小)的 k 个数。返回的结果必须要是按升序排好的。
思路一:排序
1
2
3
4
5
6
7
8
9
10
|
func findClosestElements(arr []int, k int, x int) []int {
// 按绝对值升序重排
sort.SliceStable(arr, func(i, j int) bool {
return math.Abs(float64(arr[i]-x)) < math.Abs(float64(arr[j]-x))
})
// 升序重排
arr = arr[:k]
sort.Ints(arr)
return arr
}
|
- 时间复杂度:O(nlogn),排序需要 O(nlogn)
- 空间复杂度:O(logn),排序需要 O(logn) 的栈空间
思路二:二分查找+双指针
注意:让右指针指向二分搜索结果,左指针指向二分搜索结果的前一个
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
func findClosestElements(arr []int, k int, x int) []int {
right := findX(arr, x)
left := right - 1
for i := 0; i < k; i++ {
if left < 0 {
right++
} else if right >= len(arr) || x-arr[left] <= arr[right]-x {
left--
} else {
right++
}
}
return arr[left+1 : right]
}
// 二分找x位置
func findX(arr []int, x int) int {
left, right := 0, len(arr)-1
for left <= right {
mid := left + (right-left)>>1
if arr[mid] == x {
return mid
} else if arr[mid] < x {
left = mid + 1
} else {
right = mid - 1
}
}
return left
}
|
- 时间复杂度:O(logn+k),二分查找需要 O(logn),双指针查找需要 O(k)。
- 空间复杂度:O(1)
最小区间
632. 最小区间 - 力扣(LeetCode)
有 k 个 非递减排列 的整数列表。找到一个 最小 区间,使得 k 个列表中的每个列表至少有一个数包含在其中
思路:合并标组重排+滑动窗口
首先将 k 组数据升序合并成一组,并记录每个数字所属的组,例如:
[[4,10,15,24,26],[0,9,12,20],[5,18,22,30]]
合并升序后得到:
[(0,1),(4,0),(5,2),(9,1),(10,0),(12,1),(15,0),(18,2),(20,1),(22,2),(24,0),(26,0),(30,2)]
然后只看所属组的话,那么
[1,0,2,1,0,1,0,2,1,2,0,0,2]
按组进行滑窗,保证一个窗口的组满足k组后在记录窗口的最小区间值。
1
2
3
4
5
6
7
8
9
10
11
|
[1 0 2] 2 1 0 1 0 2 1 2 0 0 2 [0, 5]
1 [0 2 1] 1 0 1 0 2 1 2 0 0 2 [0, 5]
1 0 [2 1 0] 0 1 0 2 1 2 0 0 2 [0, 5]
1 0 [2 1 0 1] 1 0 2 1 2 0 0 2 [0, 5]
1 0 [2 1 0 1 0] 0 2 1 2 0 0 2 [0, 5]
1 0 2 1 0 [1 0 2] 2 1 2 0 0 2 [0, 5]
1 0 2 1 0 1 [0 2 1] 1 2 0 0 2 [0, 5]
1 0 2 1 0 1 [0 2 1 2] 2 0 0 2 [0, 5]
1 0 2 1 0 1 0 2 [1 2 0] 0 0 2 [20, 24]
1 0 2 1 0 1 0 2 [1 2 0 0] 0 2 [20, 24]
1 0 2 1 0 1 0 2 [1 2 0 0 2] 2 [20, 24]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
func smallestRange(nums [][]int) []int {
// 哈希表存储要匹配的组
mp := make(map[int]int, len(nums))
// 合并并标组
cnt := 0
for i := range nums {
cnt += len(nums[i])
mp[i]++
}
newNums := make([][2]int, 0, cnt)
for i := range nums {
for j := range nums[i] {
newNums = append(newNums, [2]int{nums[i][j], i})
}
}
// 升序重排
sort.Slice(newNums, func(i, j int) bool {
return newNums[i][0] < newNums[j][0]
})
// 滑动窗口
res := []int{}
left := 0
// 记录还需匹配的组数
amount := len(nums)
for right := 0; right < len(newNums); right++ {
mp[newNums[right][1]]--
// 判右边界是否有效(不是多匹配的组元素)
if mp[newNums[right][1]] >= 0 {
amount--
}
// 找到一个有效区间后不断移动左边界找最小区间
for amount == 0 {
// 判结果集是否为空
if len(res) == 0 {
res = []int{newNums[left][0], newNums[right][0]}
}
res = compare(res, []int{newNums[left][0], newNums[right][0]})
mp[newNums[left][1]]++
// 判左边界是否有效
if mp[newNums[left][1]] > 0 {
amount++
}
left++
}
}
return res
}
func compare(res1, res2 []int) []int {
if res1[1]-res1[0] == res2[1]-res2[0] {
if res1[0] <= res2[0] {
return res1
} else {
return res2
}
} else if res1[1]-res1[0] < res2[1]-res2[0] {
return res1
}
return res2
}
|
- 时间复杂度:O(nlogn)
- 空间复杂度:O(n)
摆动排序 II
给一个整数数组 nums,将它重新排列成 nums[0] < nums[1] > nums[2] < nums[3]... 的顺序
思路一:排序+反转前半部分
反转前半部分:让重复元素被交叉选
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
func wiggleSort(nums []int) {
sort.Ints(nums)
temp := make([]int, len(nums))
sign := true
left, right := 0, len(nums)-1
slices.Reverse(nums[:(len(nums)+1)/2])
for i := range nums {
if sign {
temp[i] = nums[left]
left++
} else {
temp[i] = nums[right]
right--
}
sign = !sign
}
copy(nums, temp)
}
|
- 时间复杂度为O(NlogN)
- 空间复杂度为O(N)
思路二:三路划分找中位数+以中位数为基准进行一次快排划分
以中位数为基准进行一次快排划分:左边的都小于中位数,右边的都大于中位数,再交叉选即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
func wiggleSort(nums []int) {
// 快速选择算法找中位数(第len(nums)/2小)
var quickSelect func([]int, int, int, int)
quickSelect = func(nums []int, begin, end, n int) {
i, j := begin, begin
t := nums[end-1]
for j < end {
if nums[j] <= t {
nums[i], nums[j] = nums[j], nums[i]
i++
j++
} else {
j++
}
}
if i-1 > n {
quickSelect(nums, begin, i-1, n)
} else if i <= n {
quickSelect(nums, i, end, n)
}
}
midIdx := len(nums) / 2
quickSelect(nums, 0, len(nums), midIdx)
mid := nums[midIdx]
// 以中位数为基准进行一次三路划分
i, j, k := 0, 0, len(nums)-1
for j < k {
if nums[j] > mid {
nums[j], nums[k] = nums[k], nums[j]
k--
} else if nums[j] < mid {
nums[j], nums[i] = nums[i], nums[j]
i++
j++
} else {
j++
}
}
if len(nums)%2 == 1 {
midIdx++
}
// 调整中位数指针并划分数组
nums1 := make([]int, midIdx)
copy(nums1, nums[:midIdx])
nums2 := make([]int, len(nums)-midIdx)
copy(nums2, nums[midIdx:])
// 交叉选
// 对原数组进行重新排列
for i := 0; i < len(nums1); i++ {
nums[2*i] = nums1[len(nums1)-1-i]
}
for i := 0; i < len(nums2); i++ {
nums[2*i+1] = nums2[len(nums2)-1-i]
}
}
|
思路三:快速选择 + 3-way-partition + 虚地址
对前面的3-way-partition进行一定的修改,不再将小数排在左边,大数排在右边,而是将大数排在左边,小数排在右边,在这种情况下可以用一个非常简洁的公式来描述映射关系:
A[i] = nums[(1+2*(i)) % (n|1)]
``i是虚拟地址,(1+2*(i)) % (n|1)是实际地址。其中n为数组长度,|为按位或,如果n为偶数,(n|1)为n+1,如果n为奇数,(n|1)仍为n`
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
func wiggleSort(nums []int) {
n := len(nums)
// 找到中位数
// midIndex := n / 2
// sort.Ints(nums)
// mid := nums[midIndex]
// 快速选择算法找中位数(第len(nums)/2小)
var quickSelect func([]int, int, int, int)
quickSelect = func(nums []int, begin, end, n int) {
i, j := begin, begin
t := nums[end-1]
for j < end {
if nums[j] <= t {
nums[i], nums[j] = nums[j], nums[i]
i++
j++
} else {
j++
}
}
if i-1 > n {
quickSelect(nums, begin, i-1, n)
} else if i <= n {
quickSelect(nums, i, end, n)
}
}
midIdx := len(nums) / 2
quickSelect(nums, 0, len(nums), midIdx)
mid := nums[midIdx]
// 定义索引转换函数
A := func(i int) int {
return (1 + 2*(i)) % (n | 1)
}
// 三向划分实现摆动排序
i, j, k := 0, 0, n-1
for j <= k {
if nums[A(j)] > mid {
nums[A(i)], nums[A(j)] = nums[A(j)], nums[A(i)]
i++
j++
} else if nums[A(j)] < mid {
nums[A(j)], nums[A(k)] = nums[A(k)], nums[A(j)]
k--
} else {
j++
}
}
}
|
翻转对
493. 翻转对 - 力扣(LeetCode)
给定一个数组 nums ,如果 i < j 且 nums[i] > 2*nums[j] 就将 (i, j) 称作一个*重要翻转对*。返回给定数组中的重要翻转对的数量。
思路:归并排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
var res int
func reversePairs(nums []int) int {
res = 0
mergeSort(nums, 0, len(nums))
return res
}
func mergeSort(nums []int, left, right int) {
if right-left <= 1 {
return
}
mid := left + (right-left)/2
mergeSort(nums, left, mid)
mergeSort(nums, mid, right)
// 在合并的过程中,检查逆序对
j := mid
for i := left; i < mid; i++ {
// 在合并阶段统计满足 nums[i] > 2 * nums[j] 的情况
for j < right && nums[i] > 2*nums[j] {
j++
}
res += j - mid
}
merge(nums, left, mid, right)
}
func merge(nums []int, left, mid, right int) {
temp := make([]int, right-left)
copy(temp, nums[left:right])
idx1, idx2 := 0, mid-left
for i := left; i < right; i++ {
if idx1 == mid-left {
nums[i] = temp[idx2]
idx2++
} else if idx2 == right-left {
nums[i] = temp[idx1]
idx1++
} else if temp[idx1] <= temp[idx2] {
nums[i] = temp[idx1]
idx1++
} else {
nums[i] = temp[idx2]
idx2++
}
}
}
|






