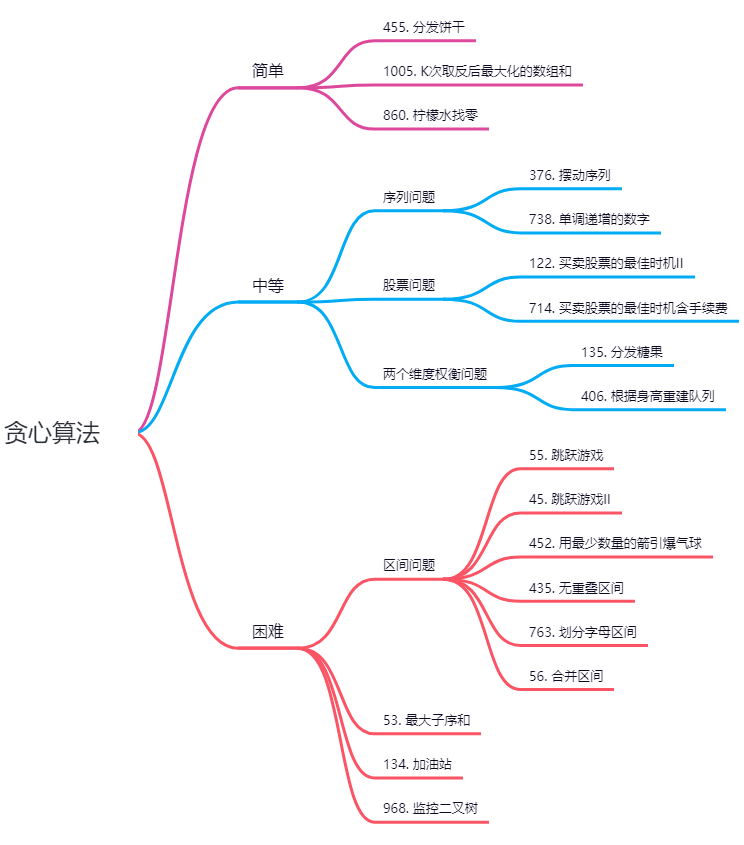
理论基础
贪心的本质是选择每一阶段的局部最优，从而达到全局最优
例如，有一堆钞票可以拿走十张，如何拿走最多的钱
每次拿最大的面额，最终就会拿走最多的钱，每次拿最大面额就是局部最优，最后拿走最多的钱就是全局最优
贪心算法并没有固定的套路
靠自己手动模拟，如果模拟可行，就可以试一试贪心策略，如果不可行，可能就需要动态规划
手动模拟一下，感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心
贪心有时候就是常识性的推导，本应该就这么做
贪心 = 常识性推导 + 举反例
分发饼干
455. 分发饼干 - 力扣（LeetCode）
给定两个数组，一个是孩子胃口值，一个是饼干满足值，每个孩子只能给一块饼干，返回最多可满足的孩子数量
贪心策略：局部最优是小饼干喂给能满足的小胃口，不浪费饼干尺寸，全局最优就是喂饱尽可能多的小孩
先对饼干、胃口从小到大排序；for循环遍历饼干，若当前饼干能满足当前胃口，则换下一胃口和下一饼干；若当前饼干无法满足当前胃口，则换下一饼干，因为当前的最小胃口都无法被满足且每个孩子只能喂一个饼干，所以需要换下一更大饼干；最后返回胃口索引即是满足的最多孩子数
注意：index要小于切片长度
1
2
3
4
5
6
7
8
9
10
11
|
func findContentChildren(g []int, s []int) int {
sort.Ints(g)
sort.Ints(s)
index := 0 // 胃口索引
for i := 0; i < len(s); i++ { // 遍历饼干
if index < len(g) && s[i] >= g[index] { // 饼干能满足胃口
index++ // 下一胃口
}
}
return index
}
|
- 时间复杂度：O(nlogn)
- 空间复杂度：O(1)
摆动序列
376. 摆动序列 - 力扣（LeetCode）
给定一个整数数组，返回数组中作为摆动序列的最长子序列长度，摆动序列是指差值正负交替出现，仅有一个/两个不等元素的序列也视作摆动序列，子序列是指原数组可删除一些元素，但元素顺序不变的序列
贪心策略：只比较当前差值与上一次异号时的差值，若俩差值异号则计数加一
本题不要求记录具体子序列，只统计具体峰值；只需要比较当前遍历到的元素和其前一元素的差值与上一次异号时的最新差值，若异号则计数加一；因为一旦差值不异号，会一直查看下一元素，说明这中间遍历过的差值一定是和上一次异号时的差值正负一样，比如三二差值和二一差值不异号，当前计数为2，一直遍历到四，四三差值和二一差值异号，说明出现峰值，则计数加一，无需再比较四三和三二差值，因为三二差值一定是和二一差值一样的；若题目要求输出最长子序列，则在遇到峰值出现时，将峰值、峰值前一个、峰值后一个元素记录即可。因为要求是摆动序列，所以坡上一定没有元素
注意：
- 剔除差值为0的情况，因为是平峰，所以不统计
- 判断差值异号：当前差值不为0且两个差值相乘≤0；因为前两个元素可能异号，所以需要用相乘≤0判断异号，这也说明正、负、零相互异号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
func wiggleMaxLength(nums []int) int {
if len(nums) == 0 || len(nums) == 1 {
return len(nums)
}
count := 1
pre := nums[1] - nums[0] // 前两个元素差值
if pre != 0 { // 前两个元素差值不为0
count++ // 计数加一
}
for i := 2; i < len(nums); i++ {
cur := nums[i] - nums[i-1] // 当前差值
if cur != 0 && cur*pre <= 0 { // 剔除差值为0的情况后新旧差值异号
count++ // 计数加一
pre = cur // 更新差值
}
}
return count
}
|
最大子序和
53. 最大子数组和 - 力扣（LeetCode）
给定一个整数数组 ，元素有正有负，返回连续子数组的最大和（子数组最少包含一个元素），子数组是数组中的一个连续部分数组
贪心策略：从头遍历数组，累加连续和，当遇到连续和为负，就将下一个元素作为起始元素重新统计连续和，在遍历过程中不断更新连续和最大值
注意：
- 统计连续和的变量用0初始化；记录最大连续和的变量用第一个元素初始化，因为当数组元素全为负数时，最大连续和一定是第一个元素而不是0
- 连续和大于最大连续和、连续和小于0这俩条件是都需要验证的，不是ifelse的关系，因为可能是负数比大小
1
2
3
4
5
6
7
8
9
10
11
12
13
|
func maxSubArray(nums []int) int {
max, sum := nums[0], 0
for i := 0; i < len(nums); i++ {
sum += nums[i] // 统计连续和
if sum > max { // 当前连续和大于最大连续和
max = sum // 更新最大连续和
}
if sum < 0 { // 连续和小于0
sum = 0 // 重新统计连续和
}
}
return max
}
|
买卖股票的最佳时机
121. 买卖股票的最佳时机 - 力扣（LeetCode）
给定一个数组，每个元素表示股票第i天的价格，不能同一天买入卖出，只能买卖一次，求最大利润，若不能获得正收益则返回0
贪心策略：从左到右枚举卖出价格 prices[i]，要想获得最大利润，需要知道第 i 天之前，股票价格的最小值是什么，也就是从 prices[0] 到 prices[i−1] 的最小值，把它作为买入价格，这可以用一个变量 minPrice 维护。
请注意，minPrice 维护的是 prices[i] 左侧元素的最小值。
由于只能买卖一次，所以在遍历中，维护 prices[i]−minPrice 的最大值，就是答案
- 时间复杂度：O(n)，其中 n 为 prices 的长度。
- 空间复杂度：O(1)。仅用到若干额外变量。
买卖股票的最佳时机II
122. 买卖股票的最佳时机 II - 力扣（LeetCode）
给定一个整数数组，表示股票每天的价格，返回最大利润，可以同一天买入卖出
贪心策略：只收集相邻两天买入卖出的正利润
本题不需要记录具体从哪天买入，在哪天卖出，所以只收集前一天买入今天卖出的正利润和即是可获得的最大利润；比如第一天买入第三天卖出利润最高，该利润其实就等于第一天买入第二天卖出再买入第三天再卖出：P[3] - P[1] = ( P[2] - P[1] ) + ( P[3] - P[2] )
1
2
3
4
5
6
7
8
9
10
|
func maxProfit(prices []int) int {
res := 0
for i := 1; i < len(prices); i++ {
profit := prices[i] - prices[i-1] // 前一天买入今天卖出的利润
if profit > 0 {
res += profit // 正利润加入结果集
}
}
return res
}
|
跳跃游戏
55. 跳跃游戏 - 力扣（LeetCode）
给定一个非负整数数组，最初位于第一个元素，元素代表在该位置能跳跃的最大长度，判断能否经过一次或多次跳跃到达最后一个元素
贪心策略：每次取最大跳跃步数（取最大覆盖范围）
for循环从头遍历，终止条件是最远能到达的位置，在遍历过程中更新最远能到达的位置，一旦最远能到达的位置可以到达最后一个元素，则返回true，若遍历到最远能到达的位置还没有到达最后一个元素，则返回false
1
2
3
4
5
6
7
8
9
10
11
12
|
func canJump(nums []int) bool {
farthest := 0 // 标记最远能到达位置
for i := 0; i <= farthest; i++ {
if i+nums[i] > farthest {
farthest = i + nums[i] // 更新能到达的最远位置
}
if farthest >= len(nums)-1 {
return true // 能到达最后一个下标
}
}
return false
}
|
跳跃游戏II
45. 跳跃游戏 II - 力扣（LeetCode）
与上一个的不同之处在于，此题统计跳到最后一个元素的最少跳跃次数
贪心策略：当前可移动距离尽可能多走，如果还没到终点，再跳跃
思路：在遍历过程中不断更新记录最远能到达的位置，若到达当前最远能到达的位置后还没到终点，则切换为记录的最远能到达的位置，重置记录的最远位置；若当前最远能到达的位置能到达终点则结束循环，切换记录的最远能到达的位置的次数就是最少跳跃次数
注意：只有一个元素时返回0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
func jump(nums []int) int {
res := 0
if len(nums) == 1 {
return res
}
curFarthest, recordFarthest := 0, 0
for i := 0; i <= curFarthest; i++ {
if i+nums[i] > recordFarthest {
recordFarthest = i + nums[i] // 更新记录的最远能达到位置
}
if curFarthest >= len(nums)-1 {
return res // 到达最后一个位置
}
if i == curFarthest { // 到达目前最远位置,但还没到最后一个位置
curFarthest = recordFarthest // 切换当前最远能到达位置
recordFarthest = 0 // 重置记录
res++ // 跳跃数+1
}
}
return res
}
|
思路二
与思路一区别是，思路二会在本次跳跃范围中发现当前最远能达到的位置能到达终点时，直接在当前跳跃数基础上加一返回；而思路一不会判断是否在本次跳跃范围中发现当前最远能达到的位置能到达终点，直到遍历完本次跳跃范围，切换到新的跳跃范围后发现能到达终点才返回
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
func jump(nums []int) int {
if len(nums) == 1 {
return 0
}
// 记录当前最远能到达的位置
farthest := 0
// 记录本跳能到达的最远位置
tempFarthest := 0
// 记录跳数
jump := 0
for i := 0; i < len(nums); i++ {
if nums[i]+i > farthest {
// 更新当前能到达的最远的位置
farthest = nums[i] + i
}
// 判断当前能到达的最远位置是否超过终点
if farthest >= len(nums)-1 {
// 直接返回当前跳数的基础上加一
return jump + 1
}
// 判断是否到达本跳的最远位置
if i == tempFarthest {
// 更新跳数
jump++
// 更新本跳的最远位置
tempFarthest = farthest
}
}
return jump
}
|
K 次取反后最大化的数组和
1005. K 次取反后最大化的数组和 - 力扣（LeetCode）
给定一个数组和取反次数k，返回用完取反次数后的最大数组和
贪心策略：优先将所有负数变为正数，再然后是最小正数
先排序，遍历数组，遇到负数若还有取反次数就取反；累加和；遍历结束后重新排序，若k有剩余为奇数就用累加和减掉二倍最小正数返回
注意：若k有剩余，则不可能剩下负数，因为遍历时遇到负数就会取反
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
func largestSumAfterKNegations(nums []int, k int) int {
sum := 0
sort.Ints(nums)
for i := 0; i < len(nums); i++ {
if nums[i] < 0 && k > 0 {
nums[i] = -nums[i] // 负数变正数
k-- // 取反次数减一
}
sum += nums[i] // 累加和
}
sort.Ints(nums)
if k%2 == 1 { // 剩下奇数次k
return sum - 2*nums[0] // 返回累加和减去二倍最小正数
}
return sum
}
|
- 时间复杂度: O(nlogn)
- 空间复杂度: O(1)
加油站
134. 加油站 - 力扣（LeetCode）
给定两个数组，一个代表加油站油量，一个代表路程花费油量，问能否环路一圈，能的话返回起始索引，否则返回-1
贪心策略：一旦从当前起始点开始累加的各站点剩余油量为负数，起始位置至少为下一位置i+1，因为[0,i]区间选择任何一个位置作为起点，到i这里都会断油
遍历站点，统计从当前起始点开始累加的各站点剩余的油量（加油 - 耗油）并累加，若累加和为负数，说明该站点油不够则选择下一站点作为新的起始位置；遍历结束，若全部站点的剩余油量累加和为负数，则说明不能走完环路；否则返回记录的起始位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
func canCompleteCircuit(gas []int, cost []int) int {
curSum, totalSum, startIndex := 0, 0, 0
for i := 0; i < len(gas); i++ {
curSum += gas[i] - cost[i] // 从当前起始点开始累加各站点剩余油量
if curSum < 0 { // 从当前起始点开始累加各站点剩余油量小于0
startIndex = i + 1 // 更新起始位置
curSum = 0 // 重置从当前起始点开始累加各站点剩余油量
}
totalSum += gas[i] - cost[i] // 统计全部站点的剩余油量
}
if totalSum < 0 { // 不足以走完环路
return -1
}
return startIndex
}
|
分发糖果
135. 分发糖果 - 力扣（LeetCode）
给定一个数组，每个元素代表孩子的评分，给每个孩子至少分发一个糖果，相邻两个孩子中分更高的的多获得一个糖果，返回需要准备的最少糖果
贪心策略：两次贪心，先确定完一边再确定另一边；只要右边评分比左边大，右边的孩子就多一个糖果；只要左边评分比右边大，左边的孩子就多一个糖果
初始给每个孩子一个糖果；从前往后遍历，遇到右比左高，就给右在左基础上加一；再从后往前遍历，遇到左比右高，此时有两种选择，一种是在右基础加+1，另一种是保持本身，因为本身是之前正序遍历时比较右大于左得到的糖果数，要保证当前孩子既保持对左多，也要比右多，只能取两种中的大值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
func candy(ratings []int) int {
candy := make([]int, len(ratings))
for i := range candy {
candy[i] = 1 // 初始化每个孩子分配一个糖果
}
for i := 1; i < len(ratings); i++ {
if ratings[i] > ratings[i-1] { // 右 > 左
candy[i] = candy[i-1] + 1 // 右 = 左 + 1
}
}
for i := len(ratings) - 2; i >= 0; i-- {
if ratings[i] > ratings[i+1] { // 左 > 右
candy[i] = max(candy[i], candy[i+1]+1)
}
}
res := 0
for i := range candy {
res += candy[i]
}
return res
}
|
柠檬水找零
860. 柠檬水找零 - 力扣（LeetCode）
给定一个数组表示每位顾客支付的钱，固定每位顾客消费五元，问能否正确找零所有顾客，能的话返回true，否则返回false，付的钱是一张 5 or 10 or 20
贪心策略：遇到账单20，优先消耗美元10，为10只能给20找零，而5可以给10和20找零，5更万能
遍历每位顾客的账单，三种情况：
- 情况一：账单是5，直接收下。
- 情况二：账单是10，消耗一个5，增加一个10
- 情况三：账单是20，优先消耗一个10和一个5，如果不够，再消耗三个5
遇到面额数不够就返回false，遍历结束返回true
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
func lemonadeChange(bills []int) bool {
five, ten := 0, 0
for i := range bills {
if bills[i] == 5 { // 情况一
five++ // 五元面额数+1
}
if bills[i] == 10 { // 情况二
if five <= 0 {
return false // 没有五元可供找零
}
ten++ // 十元面额数+1
five-- // 找零一张五元
}
if bills[i] == 20 { // 情况三
if ten > 0 && five > 0 {
ten-- // 找零一张十元
five-- // 找零一张五元
} else if five >= 3 {
five -= 3 // 找零三张五元
} else {
return false // 没有十元或足够五元可供找零
}
}
}
return true
}
|
根据身高重建队列
406. 根据身高重建队列 - 力扣（LeetCode）
给定一个二维数组，每个元素表示每人的高度和他前面高于或等于他高度的人数，按照每人的高度和其前面的人数重新排队使其符合每个元素的描述并返回
贪心策略：按照身高从大到小排序后，优先按身高高的people的k来插入，因为前面的节点一定比本节点高
两个维度的排序：先按从大到小排列身高这个维度，遇到相同身高，则前面人数小的放前面；再按前面人数k来调整插入，k是多少就插入到那个位置
注：插入操作也可以用链表实现
1
2
3
4
5
6
7
8
9
10
11
12
13
|
func reconstructQueue(people [][]int) [][]int {
sort.Slice(people, func(i, j int) bool {
if people[i][0] == people[j][0] { // 身高相同
return people[i][1] < people[j][1] // k小的在前面
}
return people[i][0] > people[j][0] // 身高大的在前面
})
for i, p := range people {
copy(people[p[1]+1:i+1], people[p[1]:i]) // 空出一个位置
people[p[1]] = p // 插入
}
return people
}
|
- 时间复杂度：O(nlog n + n2)
- 空间复杂度：O(n)
用最少数量的箭引爆气球
452. 用最少数量的箭引爆气球 - 力扣（LeetCode）
给定一个二维数组，每个元素表示一个气球，气球在该元素所示的范围内，问引爆所有气球所需最少弓箭数
贪心策略：当气球出现重叠时一起射，所用弓箭最少
将所有元素按左边界从小到大排序；遍历元素，若遇到本元素左边界大于上一个元素的右边界，则说明不重叠，弓箭数加一；否则说明重叠，更新本元素右边界为这两个元素右边界的最小值，再遍历下一元素看是否继续重叠
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
func findMinArrowShots(points [][]int) int {
sort.Slice(points, func(i, j int) bool {
return points[i][0] < points[j][0] // 左边界小的在前
})
res := 1
for i := 1; i < len(points); i++ {
if points[i][0] > points[i-1][1] { // 本元素左边界 > 上一元素右边界
res++
} else { // 有重叠
points[i][1] = min(points[i][1], points[i-1][1]) // 更新右边界
}
}
return res
}
|
- 时间复杂度：O(nlog n)，因为有一个快排
- 空间复杂度：O(1)，有一个快排，最差情况(倒序)时，需要n次递归调用。因此确实需要O(n)的栈空间
无重叠区间
435. 无重叠区间 - 力扣（LeetCode）
给定一个二维数组，每个元素表示一个范围，通过移除区间使无重叠区间，请返回最少移除数
贪心策略：将元素排序，让区间尽可能的重叠
先按左边界排序；遍历数组，遇到左区间小于上一个元素右区间说明重叠，计数加一，将该元素右边界置为两个元素中右边界小的值（代表移除）
1
2
3
4
5
6
7
8
9
10
11
12
13
|
func eraseOverlapIntervals(intervals [][]int) int {
sort.Slice(intervals, func(i, j int) bool {
return intervals[i][0] < intervals[j][0] // 左边界从小到大排序
})
res := 0
for i := 1; i < len(intervals); i++ {
if intervals[i][0] < intervals[i-1][1] { // 本元素左 < 上一元素右
res++ // 移除数+1
intervals[i][1] = min(intervals[i][1], intervals[i-1][1]) // 更新右边界
}
}
return res
}
|
- 时间复杂度：O(nlog n) ，有一个快排
- 空间复杂度：O(n)，有一个快排，最差情况(倒序)时，需要n次递归调用。因此确实需要O(n)的栈空间
划分字母区间
763. 划分字母区间 - 力扣（LeetCode）
给定一个字符串，划分尽可能多的子串，要求同一字符最多只能出现在同一子串中，且将子串顺序连接得到给定的字符串，返回一个数组表示每个子串的长度
先统计每个元素出现的最远位置，再遍历字符串，每当遍历到一个字符的最远位置 > 当前记录的最远位置，就更新当前记录的最远位置为；当遍历到当前记录的最远位置时说明成功划分一个子串，统计长度，重复此过程直到字符串遍历结束
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
func partitionLabels(s string) []int {
var endIdx [26]int
for i, char := range s {
endIdx[char-'a'] = i // 记录各字符最远位置
}
res := make([]int, 0)
startIndex := 0 // 记录子串起始位置
curMaxPosition := 0 // 记录当前最远位置
for i, char := range s {
if endIdx[char-'a'] > curMaxPosition { // 当前字符的最远位置 > 当前记录的最远位置
curMaxPosition = endIdx[char-'a'] // 更新当前记录的最远位置
}
if i == curMaxPosition { // 到达当前最远位置
res = append(res, i-startIndex+1) // 统计子串长度
startIndex = i + 1 // 设置新子串起始位置
}
}
return res
}
|
- 时间复杂度：O(n)
- 空间复杂度：O(1)，使用的数组是固定大小
合并区间
56. 合并区间 - 力扣（LeetCode）
给定一个二维数组，每个元素代表一个区间，合并重叠的区间，返回一个不重叠的区，要求恰好覆盖输入中的所有区间
先按左边界从小到大排序；遍历数组，若遇到重叠则更新本元素的右边界为两元素中右边界大的，更新本元素左边界为上一元素左区间，然后跳过本次循环遍历下一元素；若遇到本元素与上一元素不重叠则将上一元素存入结果集；遍历结束后，将最后一个元素加入结果集返回
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
func merge(intervals [][]int) [][]int {
sort.Slice(intervals, func(i, j int) bool {
return intervals[i][0] < intervals[j][0] // 按左边界从小到大排序
})
res := make([][]int, 0)
for i := 1; i < len(intervals); i++ {
if intervals[i][0] <= intervals[i-1][1] { // 本元素左边界 <= 上一元素右边界 => 重叠
intervals[i][1] = max(intervals[i][1], intervals[i-1][1]) // 更新本元素右边界
intervals[i][0] = intervals[i-1][0] // 更新本元素左边界
} else { // 不重叠
res = append(res, intervals[i-1]) // 记录上一元素
}
}
res = append(res, intervals[len(intervals)-1]) // 记录最后一个元素
return res
}
|
- 时间复杂度: O(nlogn)
- 空间复杂度: O(logn)，排序需要的空间开销
单调递增的数字
738. 单调递增的数字 - 力扣（LeetCode）
给定一个整数，返回一个小于等于该整数的最大单调递增数字
从后往前遍历，如果后一位小于前一位说明不递增，则前一位减一，后面的所有位都取最大值九
注意：
- 可以将给定数字先转为字符串再转为字符数组操作，省去对数字循环取余再除取各个位的操作
- 用一个变量保存要变九的位置，从该位开始的后面所有位都置九，初始化为数组末尾
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
func monotoneIncreasingDigits(n int) int {
if n < 10 {
return n // 个位数直接返回
}
byteNum := []byte(strconv.Itoa(n)) // 数字转为字符切片
flag := len(byteNum)
for i := len(byteNum) - 1; i > 0; i-- {
if byteNum[i] < byteNum[i-1] { // 不递增
byteNum[i-1]-- // 前一位减一
flag = i // 标记置9的起始位
}
}
for i := flag; i < len(byteNum); i++ {
byteNum[i] = '9' // 置9
}
res, _ := strconv.Atoi(string(byteNum)) // 字符切片转为数字
return res
}
|
- 时间复杂度：O(n)，n 为数字长度
- 空间复杂度：O(n)，需要一个字符串，转化为字符串操作更方便
监控二叉树
968. 监控二叉树 - 力扣（LeetCode）
给定一个二叉树，给树上节点安摄像头，摄像头可以监控自身、父节点及其直接子节点，问监控所有节点所需最少摄像头数
贪心策略：遇到叶子节点的话就在其父节点放置摄像头；之后往上每隔两个节点放置一个摄像头；充分利用摄像头监控到三层
后序遍历整个树，为每个节点填写状态，每个节点一定处于三种状态之一：无覆盖；有摄像头；有覆盖，若遍历到一个节点
- 左右孩子都有覆盖：则该节点是无覆盖状态，需要在该节点的父节点放置摄像头；因为是后序从下往上遍历，所以左右孩子有覆盖说明孩子的孩子节点一定是有摄像头的
- 左右孩子至少有一个无覆盖：则该节点置为有摄像头状态
- 左右孩子至少有一个有摄像头：则该节点是有覆盖状态
- 是空节点，则定义为有覆盖状态：若空节点定义为无覆盖状态，则其父节点应该放置摄像头，而其父节点为叶子节点，这与在叶子节点的父节点放置摄像头相矛盾；若空节点定义为有摄像头状态，则在其父节点的父节点的父节点放置摄像头，而其父节点为叶子节点，这与在叶子节点的父节点放置摄像头相矛盾
若遍历结束根节点还是无覆盖状态，则根节点置为有摄像头状态
- 递归参数和返回值：参数是当前节点；返回值是当前节点状态；结果是全局变量
- 终止条件：遇到空节点
- 单层逻辑：判断是否为空节点，若是则返回该节点为有覆盖状态；向左递归，接住返回值；向右递归，接住返回值；处理节点：若当前节点左右孩子都有覆盖，说明摄像头在孩子的孩子则当前节点返回无覆盖状态；若当前节点左右孩子至少一个无覆盖，则在当前节点放置摄像头，当前节点返回有摄像头状态；若当前节点左右孩子至少一个有摄像头，则当前节点返回有覆盖状态
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
var res int
func minCameraCover(root *TreeNode) int {
res = 0
if traversal(root) == 0 { // 根节点无覆盖
res++ // 根节点放置摄像头
}
return res
}
func traversal(cur *TreeNode) int {
if cur == nil {
return 2 // 空节点为有覆盖状态
}
left := traversal(cur.Left) // 左
right := traversal(cur.Right) // 右
if left == 2 && right == 2 { // 左右孩子有覆盖
return 0 // 当前节点无覆盖
}
if left == 0 || right == 0 { // 左右孩子至少一个无覆盖
res++ // 当前节点放置摄像头
return 1 // 当前节点有摄像头
}
return 2 // 当前节点有覆盖
}
|
- 时间复杂度: O(n)，需要遍历二叉树上的每个节点
- 空间复杂度: O(n)
Dota2 参议院
649. Dota2 参议院 - 力扣（LeetCode）
给定一个字符串，其中只包含R和D两种字符，分别代表两个阵营的参议院，每轮中每个议员可以禁止另一议员的权利或宣布胜利，失去权利的议员将在过程中被跳过，若议员发现有权利投票的议员都是 同一个阵营的 ，则可以该阵营宣布胜利，返回胜利的阵营输出，应该是 "Radiant" 或 "Dire"
思路：遍历给定字符串，分别记录两阵营议员可行使禁止权的数量和可行使投票权的数量，禁止权可继承至下一轮，投票权每轮清空，每轮结束后检查投票权看是否出现赢家；遍历议员时，若对立阵营禁止权数量非0，则该数量减一，表示本议员被对立阵营禁止权力，同时标记该议员被禁止（消灭）；若对立阵营禁止权数量数为0，则本阵营禁止权和投票权数量加一；每轮结束后判断是否出现一方投票权数量非0而另一方投票权数量为0的情况，投票权数量非0的阵营胜利
注意：标记被禁止的议员，防止干扰下一轮权力计数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
func predictPartyVictory(senate string) string {
// 分别记录两阵营可行使禁止权的数量
countBanR, countBanD := 0, 0
// 分别记录两阵营可行使投票权的数量
countVoteR, countVoteD := 0, 0
// 将不可变字符串转换为字符数组
senateB := []byte(senate)
// 不断循环直至一方宣布胜利
for {
// 遍历给定字符串
for i, ch := range senateB {
// 判断当前阵营
if ch == 'R' {
// 判断对立阵营可行使禁止权的数量是否非0
if countBanD != 0 {
// 对立阵营可行使禁止权的数量减一
countBanD--
// 消灭该议员
senateB[i] = '.'
} else {
// 本阵营可行使投票权的数量加一
countVoteR++
// 本阵营可行使禁止权的数量加一
countBanR++
}
} else if ch == 'D' {
// 判断对立阵营可行使禁止权的数量是否非0
if countBanR != 0 {
// 对立阵营可行使禁止权的数量减一
countBanR--
// 消灭该议员
senateB[i] = '.'
} else {
// 本阵营可行使投票权的数量加一
countVoteD++
// 本阵营可行使禁止权的数量加一
countBanD++
}
}
}
// 每轮结束后判断是否出现一方投票权数量非0而另一方投票权数量为0的情况
if countVoteD != 0 && countVoteR == 0 {
return "Dire"
} else if countVoteR != 0 && countVoteD == 0 {
return "Radiant"
}
// 每轮重置投票权
countVoteD, countVoteR = 0, 0
}
}
|
分割平衡字符串
1221. 分割平衡字符串 - 力扣（LeetCode）
给定一个平衡字符串，将它分割成尽可能多的平衡子字符串，返回可以通过分割得到的平衡子字符串的 最大数量
思路一：回溯（超时）
思路二：贪心：由于给定的是平衡字符串且要求分割次数最大，所以遍历字符串时，每遇到一个平衡字符串就分割，最后一定能分割成功，统计分割次数即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
func balancedStringSplit(s string) int {
res, countR, countL := 0, 0, 0
for _, ch := range s {
if ch == 'R' {
countR++
} else {
countL++
}
if countR == countL {
res++
}
}
return res
}
|
字符串中最多数目的子序列
2207. 字符串中最多数目的子序列 - 力扣（LeetCode）
给定一个字符串 text 和另一个长度为 2 的字符串 pattern ，两者都只包含小写英文字母。可以在 text 中任意位置插入 一个 字符，这个插入的字符必须是 pattern[0] 或者 pattern[1] 。注意，这个字符可以插入在 text 开头或者结尾的位置。返回插入一个字符后，text 中最多包含多少个等于 pattern 的 子序列 。子序列 指的是将一个字符串删除若干个字符后（也可以不删除），剩余字符保持原本顺序得到的字符串
思路：
- 遍历text字符串，遍历过程中统计
pattern[0]和 pattern[1]的出现次数，每遇到字符为pattern[1]就给结果累加此时pattern[0]出现的次数（贪心）；
- 由于
pattern[0] 插入text首时，可能的子序列最多（贪心），此时新出现的子序列个数为统计的pattern[1]出现的次数；pattern[1] 插入text尾时，可能的子序列最多（贪心），此时新出现的子序列个数为统计的pattern[0]出现的次数；
- 最后返回结果加上两个插入情况的最大值
注意：对于pattern[0] == pattern[1]的情况，要先判断当前字符是否为pattern[1]，在判断是否为pattern[0]，避免当前单个字符既被作为pattern[0]又被作为pattern[1]，保证更新答案时 cntX 表示的是当前字母左边的 x 的出现次数，当前字母尚未被计入cntX
1
2
3
4
5
6
7
8
9
10
11
12
13
|
func maximumSubsequenceCount(text string, pattern string) int64 {
var res, cntX, cntY int64
for i := range text {
if text[i] == pattern[1] {
res += cntX
cntY++
}
if text[i] == pattern[0] {
cntX++
}
}
return res + max(cntX, cntY)
}
|