简单记录下自己对通信序列熵概念的理解
通信函数
- 考虑了节点间的所有可能路径
- 表征任意一对节点间的全局通信能力。
通信矩阵
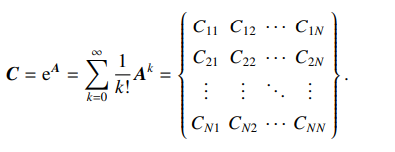
- 矩阵中的每个元素都为通信函数
- 表征所有节点间的通信能力
通信序列
-
通信序列 $$ P = {P_1, P_2, P_3, · · · , P_k , · · · , P_M} $$
-
序列P的长度为 $$ M = N(N + 1)/2 $$
-
序列中每一个元素可表示为 $$ P_k=C_{ij}/\sum{(1\leq{k}\leq{M},1\leq{i}\leq{j}\leq{N})} $$ 其中 $$ \sum=\sum_{i=1}^N\sum_{j=1}^NC_{ij} $$
$$ \sum_{k=1}^MP_k=1 $$
-
将通信矩阵的对角线及对角线上方的元素进行分析, 将这些元素进行归一化, 得到通信序列
香农熵(信息熵)
-

-
用来描述不确定事件的不确定程度,是随机变量不确定度的度量。随机变量不确定度越大,熵越大;反之越小。
通信序列熵
- 通信序列熵
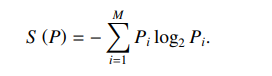
- 将通信序列的香农熵称为网络的通信序列熵