返回
Algorithm 基础能力

二进制

理论基础

异或运算⊕有以下三个性质：

  • 任何数和 0 做异或运算，结果仍然是原来的数，即 $a⊕0=a$

  • 任何数和其自身做异或运算，结果是 0，即 $a⊕a=0$

  • 异或运算满足交换律和结合律，即 $a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b$

& 表示按位与，∣ 表示按位或，⊕ ^表示按位异或，∼ 表示按位取反

移位运算：其中 << 表示左移，>> 表示右移

注：左移 𝑖 位相当于乘以 2𝑖，右移 𝑖 位相当于除以 2𝑖

只出现一次的数字

136. 只出现一次的数字 - 力扣（LeetCode）

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间

思路：数组中的全部元素的异或运算结果即为数组中只出现一次的数字。两两相同异或为0，任何数异或0为自身

1
2
3
4
5
6
7

func singleNumber(nums []int) int {
    res := nums[0]
    for i := 1; i < len(nums); i++ {
        res ^= nums[i]
    }
    return res
}

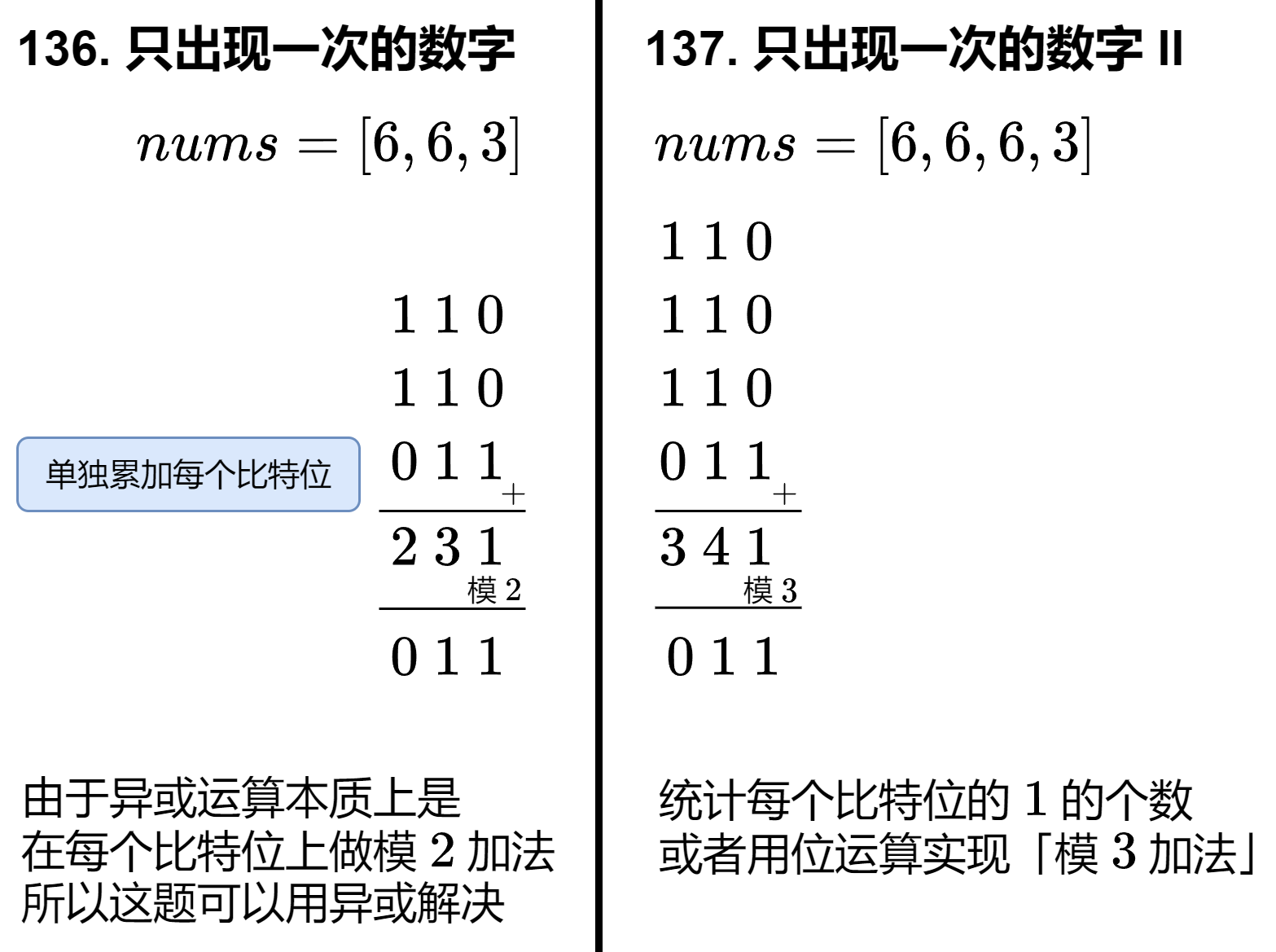
只出现一次的数字 II

137. 只出现一次的数字 II - 力扣（LeetCode）

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现三次。找出那个只出现了一次的元素。必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间

思路：

设只出现一次的那个数为 x。用二进制思考：

  • 如果 x 的某个比特是 0，由于其余数字都出现了 3 次，所以 nums 的所有元素在这个比特位上的 1 的个数是 3 的倍数。

  • 如果 x 的某个比特是 1，由于其余数字都出现了 3 次，所以 nums 的所有元素在这个比特位上的 1 的个数除 3 余 1。

这启发我们统计每个比特位上有多少个 1。下图比较了上题与本题的异同：

img 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

func singleNumber(nums []int) int {
    // 结果集初始化为一个32位整数0
    res := int32(0)
    // 遍历结果集的32个位
    for i := 0; i < 32; i++ {
        // 记录各个位上1的个数
        count := 0
        // 遍历给定数组
        for _, v := range nums {
            // 右移后累加最低位的值
            count += v >> i & 1
        }
        // 设置结果数的第i位
        res |= int32(count) % 3 << i
    }
    return int(res)
}

只出现一次的数字 III

260. 只出现一次的数字 III - 力扣（LeetCode）

给定一个非空整数数组，其中恰好有两个元素只出现一次，其余每个元素均出现两次。找出只出现一次的那两个元素。必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间

img 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

func singleNumber(nums []int) []int {
    // 保存两个结果数的异或值
    xorAll := 0
    // 遍历数组
    for _, v := range nums {
        xorAll ^= v
    }
    // 定位异或值最后一个1的索引
    idx := 0
    // 从右向左找1
    for i := 0; i < 32; i++ {
        if (xorAll >> i & 1) == 1 {
            // 保存1的索引
            idx = i
            break
        }
    }
    // 二进制 -> 十进制
    idx = 1 << idx
    res := make([]int, 2)
    // 遍历数组
    for _, v := range nums {
        // 分组异或
        if v&idx == 0 {
            res[0] ^= v
        } else {
            res[1] ^= v
        }
    }
    return res
}

位1的个数

191. 位1的个数 - 力扣（LeetCode）

给定一个十进制整数，返回其二进制形式中1的个数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

func hammingWeight(n int) int {
    res := 0
    // n循环右移直到为0
    for n != 0 {
        // 判断最低位是否为1
        if n&1 == 1 {
            res++
        }
        // n右移一位
        n >>= 1
    }
    return res
}

比特位计数

338. 比特位计数 - 力扣（LeetCode）

给定一个整数n，返回一个数组，每个元素表示0-n的每个数二进制形式中1的个数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

func countBits(n int) []int {
    res := make([]int, n+1)
    // 遍历0-n
    for i := 0; i <= n; i++ {
        // 该数循环右移直至0
        for cur := i; cur != 0; cur >>= 1 {
            // 判断最低位是否为1
            if cur&1 == 1 {
                res[i]++
            }
        }
    }
    return res
}

颠倒二进制位

190. 颠倒二进制位 - 力扣（LeetCode）

颠倒给定的 32 位无符号整数的二进制位

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

func reverseBits(num uint32) uint32 {
    newNum := uint32(0)
    // 从右向左遍历num的32位
    for i := 0; i < 32; i++ {
        // num右移一位后判断最低位是否为1
        if (num >> i & 1) == 1 {
            // 置newNum对称位为1
            newNum |= 1 << (31 - i)
        }
    }
    return newNum
}

数字范围按位与

201. 数字范围按位与 - 力扣（LeetCode）

给你两个整数 left 和 right ，表示区间 [left, right] ，返回此区间内所有数字 按位与 的结果（包含 left 、right 端点）

思路一：暴力，一个for循环遍历区间，直接按位与（超时）

1
2
3
4
5
6
7
8
9

func rangeBitwiseAnd(left int, right int) int {
    res := left
    // 遍历区间所有数字
    for i := left + 1; i <= right; i++ {
        // 按位与
        res &= i
    }
    return res
}

思路二：找公共前缀

观察按位与运算的性质，对于一列的位，只要有一个零值的位，那么这一列位的按位与运算结果都将为零。

fig1

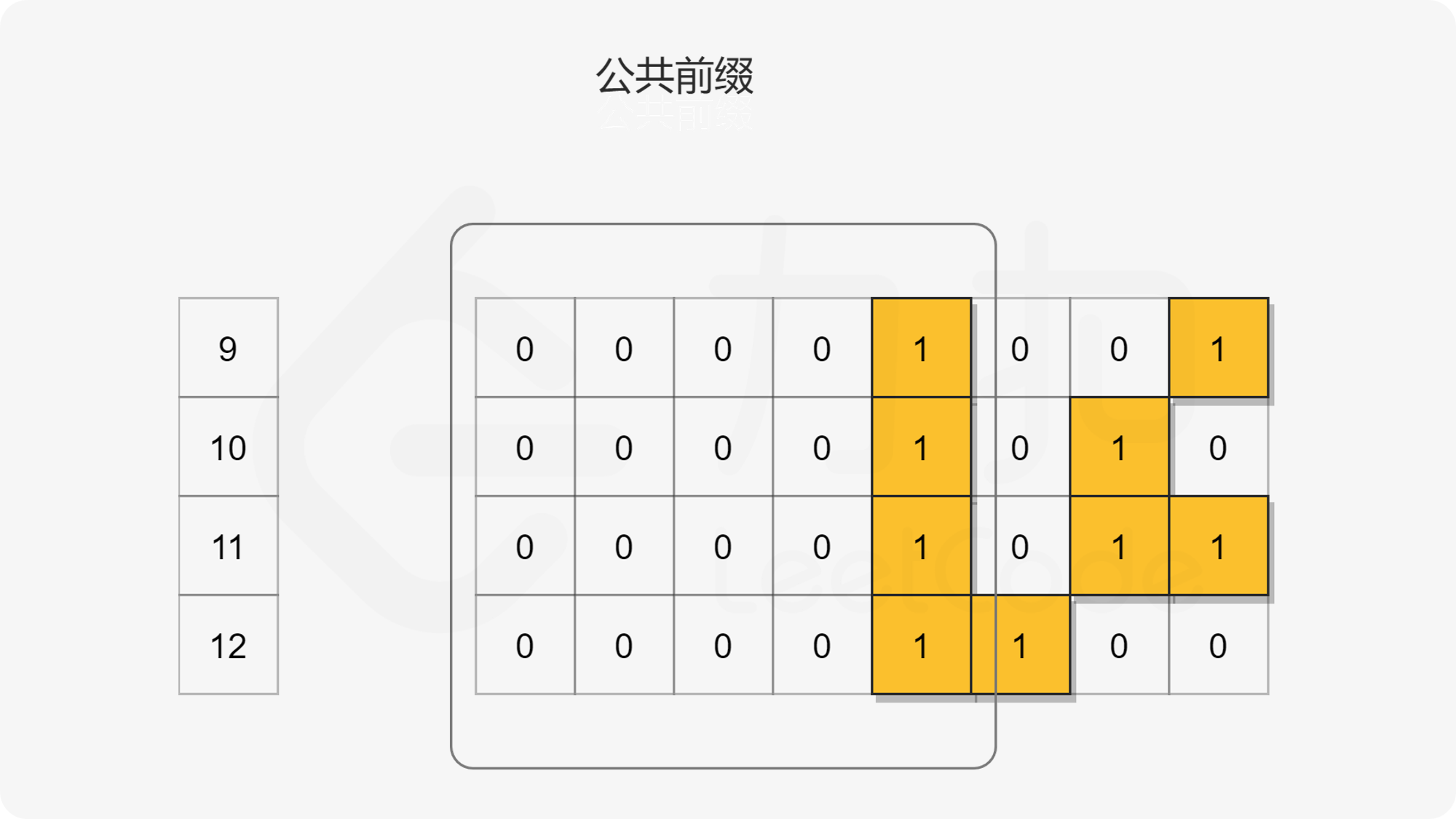
在上图中发现，对所有数字执行按位与运算的结果是所有对应二进制的公共前缀再用零补上后面的剩余位，因此，最终可以将问题重新表述为：给定两个整数，找到它们对应的二进制字符串的公共前缀

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

func rangeBitwiseAnd(left int, right int) int {
    // 记录右移的次数
    count := 0
    // 两个区间端点数字不断右移直到相等
    for left != right {
        // 右移一位
        left >>= 1
        right >>= 1
        // 右移次数加一
        count++
    }
    // 左移恢复高位
    return left << count
}

根据数字二进制下 1 的数目排序

1356. 根据数字二进制下 1 的数目排序 - 力扣（LeetCode）

给定一个整数数组，将数组中的元素按照其二进制表示中数字 1 的数目升序排序。如果存在多个数字二进制中 1 的数目相同，则必须将它们按照数值大小升序排列

思路：统计一个数的二进制中1的数量，有两种方法：

  1. 方法一：循环右移，朴实无华挨个计算1的数量
  2. 方法二：n不断与n-1做&操作，清除最低位1，操作次数就是1的个数，本方法只循环n的二进制中1的个数次，比方法一高效的多
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

func sortByBits(arr []int) []int {
    // 按照1的个数升序排列数组
    sort.Slice(arr, func(a, b int) bool {
        // 获取a和b中1的个数
        bitA := bitCount(arr[a])
        bitB := bitCount(arr[b])
        // 判断两数中1的数目是否相等
        if bitA == bitB {
            // 本身值小的在前
            return arr[a] <= arr[b]
        }
        // 1个数小的在前
        return bitA <= bitB
    })
    return arr
}
func bitCount(num int) int {
    count := 0
    // 统计num中1的个数
    for num != 0 {
        // 清除最低位1
        num &= num - 1
        // 统计1的个数
        count++
    }
    return count
}

附加

汉明距离

461. 汉明距离 - 力扣（LeetCode）

两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。给定两个整数 x 和 y，计算并返回它们之间的汉明距离

思路：记 s=x⊕y，不断地检查 s 的最低位，如果最低位为 1，那么令计数器加一，然后令 s 整体右移一位，这样 s 的最低位将被舍去，原本的次低位就变成了新的最低位。重复这个过程直到 s=0 为止。这样计数器中就累计了 s 的二进制表示中 1 的数量

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

func hammingDistance(x int, y int) int {
    res := 0
    // 更新x为x与y异或后的值
    x ^= y
    // 统计x二进制中1的个数
    for x != 0 {
        // 判x低位是否为1
        if x&1 == 1 {
            res++
        }
        // x右移一位(去除最低位)
        x >>= 1
    }
    return res
}
  • 时间复杂度：O(logC)，其中 C 是元素的数据范围，在本题中 logC=log2^31=31。
  • 空间复杂度：O(1)

找到所有数组中消失的数字

448. 找到所有数组中消失的数字 - 力扣（LeetCode）

给定一个含 n 个整数的数组 nums ，其中 nums[i] 在区间 [1, n] 内。找出所有在 [1, n] 范围内但没有出现在 nums 中的数字，并以数组的形式返回结果。**进阶：**在不使用额外空间且时间复杂度为 O(n) 的情况下解决这个问题，假定返回的数组不算在额外空间内

思路：由于 nums 的数字范围均在 [1,n] 中，可以利用这一范围之外的数字，来表达「是否存在」的含义。具体来说，遍历 nums，每遇到一个数 x，就让 nums[x−1] 增加 n。由于 nums 中所有数均在 [1,n] 中，增加以后，这些数必然大于 n。最后遍历 nums，若 nums[i] 未大于 n，就说明没有遇到过数 i+1。这样就找到了缺失的数字。

注意，当遍历到某个位置时，其中的数可能已经被增加过，因此需要对 n 取模来还原出它本来的值

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

func findDisappearedNumbers(nums []int) []int {
    res := make([]int, 0)
    // 用nums[v-1]+len(nums)标记数字v在nums中出现过
    // 遍历nums更新字典
    for _, v := range nums {
        // 还原原本的数字
        v = (v - 1) % len(nums)
        // 记入字典
        nums[v] += len(nums)
    }
    // 遍历字典找到未出现的数字计入结果集
    for i := 0; i < len(nums); i++ {
        if nums[i] <= len(nums) {
            res = append(res, i+1)
        }
    }
    return res
}
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

生命游戏

289. 生命游戏 - 力扣（LeetCode）

给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态： 1 即为 活细胞 （live），或 0 即为 死细胞 （dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：

  1. 如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；
  2. 如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；
  3. 如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；
  4. 如果死细胞周围正好有三个活细胞，则该位置死细胞复活；

下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态，返回下一个状态。

思路：二进制位存储下一状态

由于每个位置的细胞的状态是取决于当前四周其他状态的，而且每个细胞的状态是同时变化的，所以不能一个一个地更新，只能在一个新的数组里创建新的状态。因为这道题目的输入是int[][]，而int是可以存储更多的比特位的。原有的最低位存储的是当前状态，那倒数第二低位存储下一个状态就行了。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

var DX = [8]int{-1, -1, -1, 0, 0, 1, 1, 1}
var DY = [8]int{-1, 0, 1, -1, 1, -1, 0, 1}

func gameOfLife(board [][]int) {
    for i := range board {
        for j := range board[i] {
            // 统计当前细胞周围的活细胞数
            cnt := 0
            // 遍历周围八个细胞
            for k := 0; k < 8; k++ {
                x := i + DX[k]
                y := j + DY[k]
                // 判是否为活细胞
                if x >= 0 && x < len(board) && y >= 0 && y < len(board[0]) && (board[x][y]&1) == 1 {
                    cnt++
                }
            }
            // 判当前是否为死细胞且周围正好有三个活细胞
            if board[i][j] == 0 && cnt == 3 {
                // 变活细胞 下一状态保存在第二比特位10
                board[i][j] |= 2
            }
            // 判当前是否为活细胞且周围有两/三个活细胞
            if board[i][j] == 1 && (cnt == 2 || cnt == 3) {
                // 下一状态仍为活细胞11
                board[i][j] |= 3
            }
            // 死细胞00周围无三个活细胞 下一状态仍为死细胞00 (无需显式赋值)
            // 活细胞01周围无两/三个活细胞 下一状态为死细胞01 (无需显式赋值)
        }
    }
    // 统一更新至下一状态
    for i := range board {
        for j := range board[i] {
            board[i][j] >>= 1
        }
    }
}
© 2021 - 2024 YI · 0 Days
共叭叭了 2154042字 · 172篇文章

Built with Hugo
Theme Stack designed by Jimmy