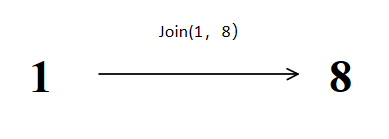理论基础
二叉树和回溯算法章节中已经讲过深搜和广搜,二叉树的遍历就是深搜和广搜在二叉树结构上的应用, 而回溯算法本身就是深搜,只不过利用其回溯的过程。在图论中,深搜和广搜就是在图上的遍历,图的存储方式一般是 邻接表和邻接矩阵。
dfs 与 bfs 区别
深度优先搜索(dfs)和广度优先搜索(bfs)区别:
- dfs是可一个方向去搜,不到黄河不回头,直到遇到绝境了,搜不下去了,再换方向(换方向的过程就涉及到了回溯)。
- bfs是先把本节点所连接的所有节点遍历一遍,走到下一个节点的时候,再把连接节点的所有节点遍历一遍,搜索方向更像是广度,四面八方的搜索过程。
dfs模板
正是因为dfs搜索可一个方向,并需要回溯,所以用递归的方式来实现是最方便的。回溯操作就在递归函数的下面,递归和回溯是相辅相成的。
1
2
3
4
5
6
7
8
9
10
11
12
|
void dfs(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本节点所连接的其他节点) {
处理节点;
dfs(图,选择的节点); // 递归
回溯,撤销处理结果
}
}
|
深搜三部曲
- 确认递归函数,参数:在写递归函数的过程中,发现需要什么参数,再去补充;一般深搜需要 二维数组数组结构保存所有路径,需要一维数组保存单一路径
- 确认终止条件:终止条件不仅是结束本层递归,同时也是收获结果的时候;很多dfs写法,没有写终止条件,其实终止条件写在了下面dfs递归的逻辑里了,也就是不符合条件,直接不会向下递归
- 处理目前搜索节点出发的路径:一般这里就是一个for循环的操作,去遍历 目前搜索节点 所能到的所有节点
广搜的使用场景
广搜的搜索方式就适合于解决两个点之间的最短路径问题
因为广搜是从起点出发,以起始点为中心一圈一圈进行搜索,一旦遇到终点,记录之前走过的节点就是一条最短路。
当然,也有一些问题是广搜 和 深搜都可以解决的,例如岛屿问题,这类问题的特征就是不涉及具体的遍历方式,只要能把相邻且相同属性的节点标记上就行。
代码框架
很多网上的资料都是直接说BFS用队列来实现,其实仅仅需要一个容器能保存遍历过的元素就可以,用队列,还是用栈,甚至用数组,都是可以的。
用队列的话,就是保证方向统一,例如统一顺时针或者逆时针,因为队列是先进先出,所以加入元素和弹出元素的顺序是没有改变的
如果用栈的话,就是第一圈是方向1,第二圈是反方向,第三圈又回到方向1。,因为栈是先进后出,加入元素和弹出元素的顺序改变了
那么广搜需要注意搜索的顺序吗? 不需要!所以用队列,还是用栈都是可以的,但大家都习惯用队列了,所以下面也用队列来给出广搜代码模板
1
2
3
4
5
6
7
8
9
10
11
|
func bfs(参数) {
// 定义队列
// 起始节点入队
for len(queue) != 0 {
// 取队首元素
for 选择:本节点所连接的其他节点 {
// 处理节点
// 新节点入队
}
}
}
|
并查集
并查集用来解决连通性问题:判断两个元素是否在同一个集合里
- 将两个元素添加到一个集合中
- 判断两个元素是否在一个集合
原理
将A,B两个元素放在同一集合(连通),只需要用一个一维数组来表示,即father[A] = B,father[B] = B,这样就表示AB连通了;根据A可以找到B,根据B可以找到B,AB最终都会找到B,即AB同根,表示两个元素在一个集合里
同理,将A,B,C三个元素放在同一个集合(连通),即:father[A] = B,father[B] = C,father[C] = C,这样就表示ABC连通了;根据A可以找到B,根据B可以找到C,根据C可以找到C,ABC最终都会找到C,即ABC同根,表示三个元素在一个集合里,寻根过程:
1
2
3
4
|
func find(u int) int {
if father[u] == u return u // 如果根就是自己,直接返回
else return find(father[u]) // 如果根不是自己,就根据数组下标一层一层向下找根
}
|
father数组初始化的时候要 father[i] = i,默认自己指向自己
判断两个元素是否在同一个集合里,若通过find函数找到两个元素属于同一个根的话,那么这两个元素就是同一个集合,代码如下:
1
2
3
4
5
|
func isSame(a int, b int) bool {
a = find(a)
b = find(b)
return a == b
}
|
路径压缩
如果让所有节点都直接挂载根下,这样在寻根的时候就只需要一步,想要达到这样的效果,就需要 路径压缩,将非根节点的所有节点直接指向根节点。
实现:在递归的过程中,让 father[u] 接住递归函数 find(father[u]) 的返回结果
因为 find 函数向上寻找根节点时,father[u] 表示 u 的父节点,那么让 father[u] 直接获取find函数返回的根节点,这样就让根节点直接作为了节点 u 的父节点
1
2
3
4
5
|
// 并查集里寻根的过程
func find(u int) int {
if father[u] == u return u
else return father[u] = find(father[u]) // 路径压缩
}
|
并查集模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
var father []int
func validPath(n int, edges [][]int, source int, destination int) bool {
father = make([]int, n)
initial(n)
for i := range edges {
join(edges[i][0], edges[i][1])
}
return isSame(source, destination)
}
// 并查集初始化
func initial(n int) {
for i := 0; i < n; i++ {
father[i] = i
}
}
// 并查集里寻根
func find(u int) int {
if father[u] == u {
return u
}
father[u] = find(father[u])
return father[u]
}
// 判断a和b是否找到同一个根
func isSame(a int, b int) bool {
// 找到a,b的根
a = find(a)
b = find(b)
return a == b
}
// 边a->b加入并差集
func join(a int, b int) {
a = find(a)
b = find(b)
if a == b {
return // 同根说明已经在一个集合里
}
father[a] = b
}
|
注意:join函数里要有find函数进行寻根的过程,这样就保证元素在有向图里是强连通的;也要接收保存find寻根的返回值,用路径压缩后的父节点连接
模拟过程
1、join(1, 8)
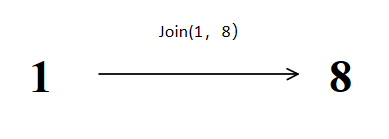
2、join(3, 8)
3指向1不指向8是因为在join函数里分别对3和8寻根之后,3的根为3,8的根为1,再进行关联就为3指向1
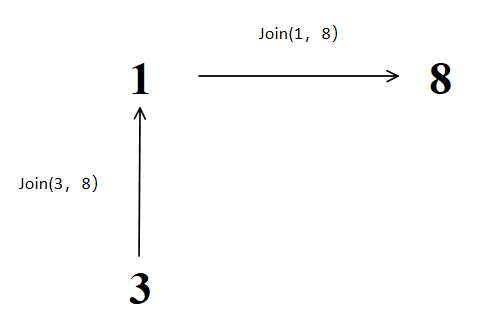
3、join(1, 7)
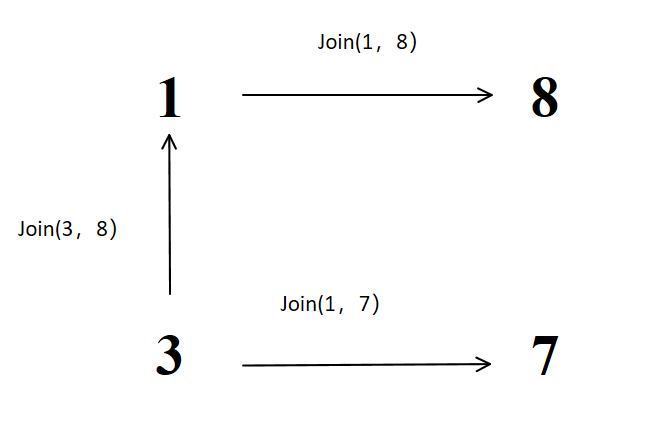
4、join(8, 5)
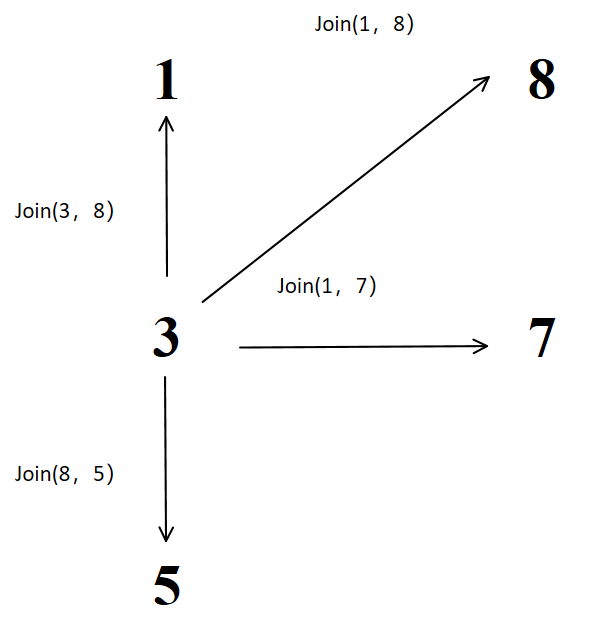
这里8的根是3,那么3应该指向5,因为是在join函数里分别对a和b进行了寻根之后再进行的关联
但是这里1不指向8了,3直接指向了8,这是因为路经压缩,这减少了下次查询的路径长度
5、join(2, 9)
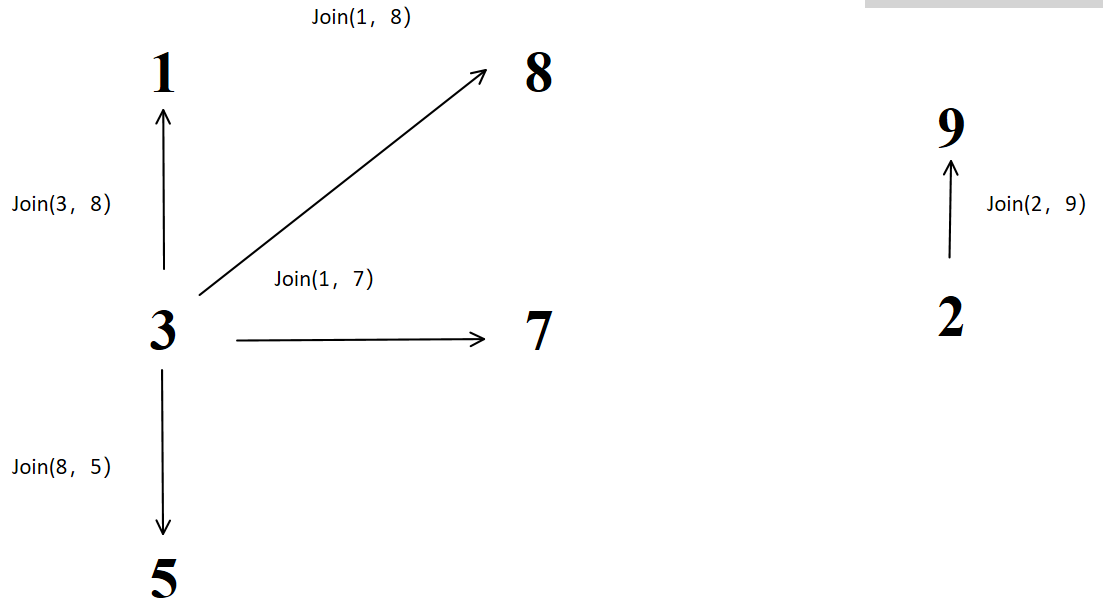
6、join(6, 9)
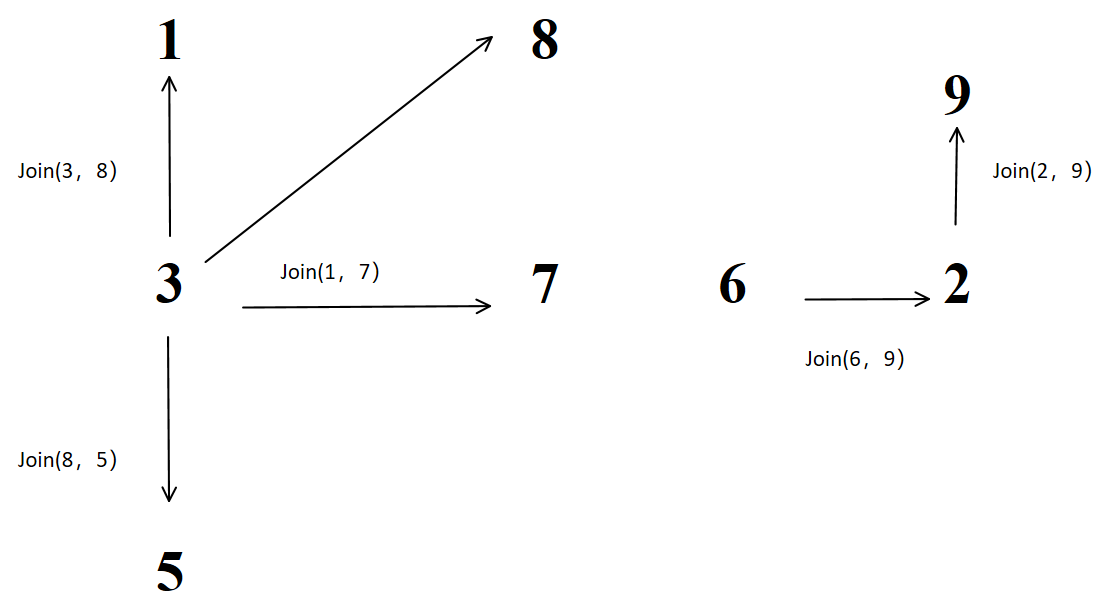
因为9的根为 2,所以用6指向2
13578是同一个集合,269是同一个集合
复杂度分析
路径压缩版并查集
- 空间复杂度: O(n) ,申请一个father数组
- 路径压缩后的并查集时间复杂度在O(logn)与O(1)之间,且随着查询或者合并操作的增加,时间复杂度会越来越趋于O(1)
在第一次查询的时候,相当于是n叉树上从叶子节点到根节点的查询过程,时间复杂度是logn,但路径压缩后,后面的查询操作都是O(1),而 join 函数和 isSame函数里涉及的查询操作也是一样的过程
所有可能的路径
797. 所有可能的路径 - 力扣(LeetCode)
给定一个二维数组含有n个元素,表示有向无环图,每个元素表示该元素下标节点能到达的节点(一条有向边),返回节点0到节点n-1的所有路径
- 确认递归函数,参数:一个图是用来遍历,一个是目前遍历的节点;单一路径和路径集合可以放在全局变量
- 确认终止条件:当目前遍历的节点为最后一个节点的时候,就找到了一条从出发点到终止点的路径
- 处理目前搜索节点出发的路径:得到当前遍历节点的指向的下一个节点,将选中的节点加入到单一路径中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
var path []int // 节点0到节点n-1的所有路径
var res [][]int // 节点0到节点n-1的一条路径
func allPathsSourceTarget(graph [][]int) [][]int {
path = make([]int, 0) // 力扣中全局变量需要重新初始化,否则会携带之前测试case的答案
res = make([][]int, 0)
path = append(path, 0) // 从节点0出发
dfs(graph, 0)
return res
}
func dfs(graph [][]int, cur int) {
// 终止条件:当前遍历节点是节点n-1
if cur == len(graph)-1 {
temp := make([]int, len(path))
copy(temp, path)
res = append(res, temp) // 将找到的一条路径加入结果集
return
}
for i := 0; i < len(graph[cur]); i++ { // 遍历当前节点连接的所有节点
path = append(path, graph[cur][i]) // 将遍历到的节点加入路径
dfs(graph, graph[cur][i]) // 进入下一层递归
path = path[:len(path)-1] // 回溯 在路径中撤销本节点
}
}
|
岛屿数量
200. 岛屿数量 - 力扣(LeetCode)
给定一个二维数组,表示一块区域;元素由0和1组成,1代表陆地,0代表海洋;若陆地被海洋包裹,则说明是岛屿;假设该区域四条边外是海洋;被海洋包裹的多块水平或垂直相连陆地看作一个岛屿;返回该区域中岛屿的数量
本题思路:遍历一遍所有节点;每遇到一个陆地节点且没有被标记过,计数器就加一,然后把该陆地节点所能遍历到的陆地都标记上;在遇到标记过的陆地节点和海洋节点的时候直接跳过;这样计数器就是最终岛屿的数量
把陆地节点所能遍历到的陆地都标记上可以使用 DFS,BFS或者并查集
对于本题来说,DFS和BFS都是对一个节点进行四周遍历,区别是DFS用递归栈来保存遍历过的状态,BFS用队列来保存遍历过的状态
DFS(推荐下面第二种优化后的写法)
- 确认递归函数,参数:一个是图用来遍历,一个是目前遍历的节点的横纵坐标(坐标用来访问四周节点和设置标记节点变量);保存节点标记的变量可以放在全局变量
- 确认终止条件:索引越界或遇到海洋
- 处理目前搜索节点出发的路径:得到当前遍历节点的指向的下一个节点
注意:本题是网格,dfs时要四个方向都搜
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
var visited [][]bool
func numIslands(grid [][]byte) int {
res := 0
visited = make([][]bool, len(grid))
for i := range visited {
visited[i] = make([]bool, len(grid[i]))
}
for i := range grid {
for j := range grid[i] {
if grid[i][j] == '1' && !visited[i][j] { // 遇到陆地节点且没有被标记过
res += 1
dfs(grid, i, j)
}
}
}
return res
}
func dfs(grid [][]byte, x int, y int) {
if grid[x][y] == '0' || visited[x][y] { // 遇到海洋节点或标记过的节点
return
}
visited[x][y] = true // 标记节点
if x != len(grid)-1 { // x没到最后一层
dfs(grid, x+1, y) // 递归 向下探索
}
if y != len(grid[x])-1 { // y没到最后一列
dfs(grid, x, y+1) // 递归 向右探索
}
if x != 0 { // x不是第一层
dfs(grid, x-1, y) // 递归 向上探索
}
if y != 0 { // y不是第一列
dfs(grid, x, y-1) // 递归 向左探索
}
}
|
DFS优化:将遍历过的陆地直接置为0
注意:在终止条件中,先判断索引,再判断是否遇到海洋,防止越界;同理由于判断列数要用到行数,所有也要放在行数判断之后
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
func numIslands(grid [][]byte) int {
res := 0
for i := range grid {
for j := range grid[i] {
if grid[i][j] == '1' { // 遇到陆地节点且没有被标记过
res += 1
dfs(grid, i, j)
}
}
}
return res
}
func dfs(grid [][]byte, x int, y int) {
// 下标越界或遇到海洋节点
if x < 0 || y < 0 || x == len(grid) || y == len(grid[x]) || grid[x][y] == '0' {
return
}
grid[x][y] = '0' // 标记节点
dfs(grid, x+1, y) // 递归 向下探索
dfs(grid, x, y+1) // 递归 向右探索
dfs(grid, x-1, y) // 递归 向上探索
dfs(grid, x, y-1) // 递归 向左探索
}
// 写法二:更通用
var dis = [4][2]int{{1, 0}, {-1, 0}, {0, 1}, {0, -1}}
func numIslands(grid [][]byte) int {
res := 0
for i := range grid {
for j := range grid[i] {
if grid[i][j] == '1' {
res++
dfs(grid, i, j)
}
}
}
return res
}
func dfs(grid [][]byte, i, j int) {
grid[i][j] = 'x'
for _, offset := range dis {
x := i + offset[0]
y := j + offset[1]
if x >= 0 && x < len(grid) && y >= 0 && y < len(grid[0]) && grid[x][y] == '1' {
dfs(grid, x, y)
}
}
}
|
BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
func numIslands(grid [][]byte) int {
res := 0
for i := range grid {
for j := range grid[i] {
if grid[i][j] == '1' { // 遇到陆地节点且没有被标记过
res += 1
bfs(grid, i, j)
}
}
}
return res
}
func bfs(grid [][]byte, x int, y int) {
queue := make([][]int, 0) // 定义队列
queue = append(queue, []int{x, y}) // 起始节点入队
move := [4][2]int{{1, 0}, {0, 1}, {0, -1}, {-1, 0}} // 下右左上
for len(queue) != 0 { // 遍历队列
node := queue[0] // 取队首元素
queue = queue[1:] // 更新队列
for i := 0; i < 4; i++ { // 遍历当前节点四周
x = node[0] + move[i][0]
y = node[1] + move[i][1]
// 下标越界或遇到海洋节点
if x < 0 || y < 0 || x == len(grid) || y == len(grid[x]) || grid[x][y] == '0' {
continue
}
grid[x][y] = '0' // 标记节点
queue = append(queue, []int{x, y}) // 入队
}
}
}
|
岛屿的最大面积
695. 岛屿的最大面积 - 力扣(LeetCode)
给定一个二维数组,表示一块区域;元素由0和1组成,1代表陆地,0代表海洋;若陆地被海洋包裹,则说明是岛屿;假设该区域四条边外是海洋;被海洋包裹的多块水平或垂直相连陆地看作一个岛屿;返回该区域中岛屿的最大面积
本题思路:遍历一遍所有节点;每遇到一个陆地节点且没有被标记过,说明是新岛屿,然后把该陆地节点所能遍历到的陆地都标记上;在遇到标记过的陆地节点和海洋节点的时候直接跳过;在标记时统计该岛屿的面积,遍历该岛屿结束后,与已保存的最大岛屿面积作比较取最大值,
把陆地节点所能遍历到的陆地都标记上可以使用 DFS,BFS或者并查集
对于本题来说,DFS和BFS都是对一个节点进行四周遍历,区别是DFS用递归栈来保存遍历过的状态,BFS用队列来保存遍历过的状态
DFS
- 递归参数:一个是图用来遍历,一个是目前遍历的节点的横纵坐标(坐标用来访问四周节点),记录每个岛屿面积的变量可设为全局
- 确认终止条件:索引越界或遇到海洋
- 处理目前搜索节点出发的路径:得到当前遍历节点的指向的下一个节点
注意:每次遍历完岛屿并记录结束后,要清空全局变量,使其在下次岛屿遍历中记录
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
var area int
func maxAreaOfIsland(grid [][]int) int {
res := 0
for i := range grid {
for j := range grid[i] {
if grid[i][j] == 1 {
dfs(grid, i, j)
res = max(res, area)
area = 0 // 重置面积
}
}
}
return res
}
func dfs(grid [][]int, x int, y int) {
if x < 0 || y < 0 || x == len(grid) || y == len(grid[x]) || grid[x][y] == 0 {
return
}
grid[x][y] = 0 // 标记
area += 1 // 统计面积
dfs(grid, x+1, y) // 下
dfs(grid, x, y+1) // 右
dfs(grid, x-1, y) // 上
dfs(grid, x, y-1) // 左
}
// 写法二:更通用
var dis = [4][2]int{{1, 0}, {-1, 0}, {0, 1}, {0, -1}}
var res int
var cnt int
func maxAreaOfIsland(grid [][]int) int {
res = 0
cnt = 0
for i := range grid {
for j := range grid[i] {
if grid[i][j] == 1 {
dfs(grid, i, j)
res = max(res, cnt)
cnt = 0
}
}
}
return res
}
func dfs(grid [][]int, i, j int) {
grid[i][j] = 0
cnt++
for _, offset := range dis {
x := i + offset[0]
y := j + offset[1]
if x >= 0 && x < len(grid) && y >= 0 && y < len(grid[0]) && grid[x][y] == 1 {
dfs(grid, x, y)
}
}
}
|
飞地的数量
1020. 飞地的数量 - 力扣(LeetCode)
给定一个二维数组,表示一块区域;元素由0和1组成,1代表陆地,0代表海洋;若陆地被海洋包裹,则说明是岛屿;假设该区域四条边外是海洋;被海洋包裹的多块水平或垂直相连陆地看作一个岛屿;返回该区域中所有不能到达矩阵边界的岛屿的面积总和
本题思路一:遍历一遍所有节点;每遇到一个陆地节点且没有被标记过,说明是新岛屿,然后把该陆地节点所能遍历到的陆地都标记上;在遇到标记过的陆地节点和海洋节点的时候直接跳过;在标记时统计该岛屿的面积,同时检查该节点是否到达边界,一旦该岛屿可以到达边界则标记该岛屿;遍历该岛屿结束后,若该岛屿不能到达边界,则将该岛屿面积记入结果集
思路二:本题要求找到不靠边的陆地面积,那么我们只要从周边找到陆地然后 通过 dfs 或者 bfs 将周边靠陆地且相邻的陆地都变成海洋,然后再去重新遍历地图的时候,统计此时还剩下的陆地就可以了。
把陆地节点所能遍历到的陆地都标记上可以使用 DFS,BFS或者并查集
对于本题来说,DFS和BFS都是对一个节点进行四周遍历,区别是DFS用递归栈来保存遍历过的状态,BFS用队列来保存遍历过的状态
思路一DFS
- 递归参数:一个是图用来遍历,一个是目前遍历的节点的横纵坐标(坐标用来访问四周节点),记录每个岛屿面积的变量和标记该岛屿能否到达矩阵边界的变量可设为全局
- 确认终止条件:索引越界或遇到海洋
- 处理目前搜索节点出发的路径:得到当前遍历节点的指向的下一个节点
注意:每次遍历完岛屿并记录结束后,要清空全局变量,使其在下次岛屿遍历中记录
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
var area int
var arrived bool
func numEnclaves(grid [][]int) int {
res := 0
for i := range grid {
for j := range grid[i] {
if grid[i][j] == 1 {
dfs(grid, i, j)
if !arrived {
res += area // 记录不能到达边界的面积
}
area = 0 // 重置
arrived = false // 重置
}
}
}
return res
}
func dfs(grid [][]int, x int, y int) {
if x < 0 || y < 0 || x == len(grid) || y == len(grid[x]) {
arrived = true // 上一块陆地是边界
return
}
if grid[x][y] == 0 {
return
}
grid[x][y] = 0 // 标记
area += 1 // 统计面积
dfs(grid, x+1, y) // 下
dfs(grid, x, y+1) // 右
dfs(grid, x-1, y) // 上
dfs(grid, x, y-1) // 左
}
|
思路二DFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
func numEnclaves(grid [][]int) int {
m, n := len(grid), len(grid[0])
for i := 0; i < m; i++ {
if grid[i][0] == 1 { // 第一列
dfs(grid, i, 0)
}
if grid[i][n-1] == 1 { // 最后一列
dfs(grid, i, n-1)
}
}
for i := 0; i < n; i++ {
if grid[0][i] == 1 { // 第一排
dfs(grid, 0, i)
}
if grid[m-1][i] == 1 { // 最后一排
dfs(grid, m-1, i)
}
}
res := 0
for i := range grid {
for j := range grid[i] {
if grid[i][j] == 1 {
res++
}
}
}
return res
}
func dfs(grid [][]int, x, y int) {
if x < 0 || y < 0 || x == len(grid) || y == len(grid[0]) || grid[x][y] == 0 {
return
}
grid[x][y] = 0
dfs(grid, x+1, y)
dfs(grid, x, y+1)
dfs(grid, x-1, y)
dfs(grid, x, y-1)
}
|
被围绕的区域
130. 被围绕的区域 - 力扣(LeetCode)
给定一个二维数组,表示一块区域;元素由x和o组成,o代表陆地,x代表海洋;若陆地被海洋包裹,则说明是岛屿;假设该区域四条边外是海洋;被海洋包裹的多块水平或垂直相连陆地看作一个岛屿;将该区域中所有不能到达矩阵边界的岛屿的都置为海洋
思路:遍历地图周边一圈,将与周边相邻的’O’都改成’A',然后再遍历一遍地图,遇到的 ‘O’ 一定都是地图中间的’O',全部改成’X',遇到’A’全部改回’O'
把陆地节点所能遍历到的陆地都标记上可以使用 DFS,BFS或者并查集
对于本题来说,DFS和BFS都是对一个节点进行四周遍历,区别是DFS用递归栈来保存遍历过的状态,BFS用队列来保存遍历过的状态
- 递归参数:一个是图用来遍历,一个是目前遍历的节点的横纵坐标(坐标用来访问四周节点),记录标记过的陆地的变量可设为全局
- 确认终止条件:索引越界或遇到海洋
- 处理目前搜索节点出发的路径:得到当前遍历节点的指向的下一个节点
注意:
- 标记可到边界的陆地可直接将该陆地置为其他值,后面遍历区域时再将其恢复;用此方法时注意最后遍历时要用
if elseif;
- DFS中遇到标记过的变量也要返回,不然会陷入死循环,一直标记标记过的变量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
func solve(board [][]byte) {
for row := 0; row < len(board); row++ {
if board[row][0] == 'O' { // 第一列
dfs(board, row, 0)
}
if board[row][len(board[0])-1] == 'O' { // 最后一列
dfs(board, row, len(board[0])-1)
}
}
for col := 1; col < len(board[0])-1; col++ {
if board[0][col] == 'O' { // 第一排去首尾剩下中间的
dfs(board, 0, col)
}
if board[len(board)-1][col] == 'O' { // 最后一排去首尾剩下中间的
dfs(board, len(board)-1, col)
}
}
for i := range board {
for j := range board[i] {
if board[i][j] == 'A' {
board[i][j] = 'O' // 恢复可以到达边界的陆地
} else if board[i][j] == 'O' {
board[i][j] = 'X' // 不能到达边界的陆地
}
}
}
}
func dfs(board [][]byte, x int, y int) {
if x < 0 || y < 0 || x == len(board) || y == len(board[x]) || board[x][y] == 'X' || board[x][y] == 'A' {
return
}
board[x][y] = 'A' // 标记该陆地
dfs(board, x+1, y) // 下
dfs(board, x, y+1) // 右
dfs(board, x-1, y) // 上
dfs(board, x, y-1) // 左
}
|
太平洋大西洋水流问题
417. 太平洋大西洋水流问题 - 力扣(LeetCode)
给定一个二维数组,表示一块岛屿,该岛屿左方和上方被太平洋包围,右方和下方被大西洋包围;每个元素表示每块陆地的高度,水可以从高流向相等或小于的陆地;水到岛屿边缘就可以直接入海;返回可以同时流入大西洋和太平洋的陆地坐标
思路:反过来想,从太平洋边上的节点 逆流而上,将遍历过的节点都标记上;从大西洋的边上节点 逆流而上,将遍历过的节点也标记上; 最后遍历岛屿,两方都标记过的节点就是既可以流到太平洋也可以流到大西洋的陆地
用一个三维数组来标记节点,前两个维度标记节点横纵坐标,第三个维度长度为2标记节点能否到达太平洋或大西洋,可作为全局变量;dfs时第三维作为入参标记当前从哪个洋逆流而上
dfs遍历时,需要当前节点和下一个节点的状态比较,可以先比较再决定是否递归遍历,这就需要四个偏移量来计算向四周移动后的坐标,遍历四个偏移量来表示向四周遍历
DFS
注意:
- 先遍历第一列太平洋和最后一列大西洋后,再次遍历排时仍要从当前排第一个元素出发,因为副对角俩元素可以同时到达两个洋
- 由于是在循环中遍历四个方向所以是跳过本次循环,不是
return返回
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
var visited [][][]bool
func pacificAtlantic(heights [][]int) [][]int {
m := len(heights)
n := len(heights[0])
visited = make([][][]bool, m)
for i := range visited {
visited[i] = make([][]bool, n)
}
for i := range visited {
for j := range visited[i] {
visited[i][j] = make([]bool, 2)
}
}
// 遍历首尾行,标记洋能到的区域
for i := 0; i < n; i++ {
dfs(heights, 0, i, 0)
dfs(heights, m-1, i, 1)
}
// 遍历首尾列,标记洋能到的区域
for i := 0; i < m; i++ {
dfs(heights, i, 0, 0)
dfs(heights, i, n-1, 1)
}
// 遍历矩阵,找两个洋都能到的
res := [][]int{}
for i := range heights {
for j := range heights[i] {
if visited[i][j][1] && visited[i][j][0] {
res = append(res, []int{i, j})
}
}
}
return res
}
var dis = [4][2]int{{1, 0}, {-1, 0}, {0, 1}, {0, -1}}
func dfs(heights [][]int, i, j, sign int) {
visited[i][j][sign] = true
for _, offset := range dis {
x := i + offset[0]
y := j + offset[1]
if x >= 0 && x < len(heights) && y >= 0 && y < len(heights[0]) && heights[x][y] >= heights[i][j] && !visited[x][y][sign] {
dfs(heights, x, y, sign)
}
}
}
|
最大人工岛
827. 最大人工岛 - 力扣(LeetCode)
给定一个二维数组,表示一块区域;元素由0和1组成,1代表陆地,0代表海洋;若陆地被海洋包裹,则说明是岛屿;假设该区域四条边外是海洋;被海洋包裹的多块水平或垂直相连陆地看作一个岛屿;现在可以改变一个海洋使其变为陆地,返回改变后的最大岛屿面积
思路:
- 遍历地图一次,得出各个岛屿的面积,并做编号记录,可以使用map记录,key为岛屿编号,value为岛屿面积
- 再遍历地图一次,遇到 0 就统计其四周相邻岛屿的面积(用到上一步记录好的岛屿面积),将面积加在一起后,再加一得到一个总面积,遍历所有 0 之后,就可以得出一个最大人工岛
优化:第一次遍历时可以直接修改原数组的元素值作为标记,在遍历完一个岛屿后统计其面积,并将标记值加一
注意:
- 第二次遍历统计
0四周岛屿面积时需要再用一个map记录该岛屿是否被统计过,因为有的岛屿可能占用0四周的多个陆地,若不记录,则同一岛屿可能被同一0统计多次
- 最后返回结果需要判断结果是否为
0,若结果是0,说明该区域全是陆地1,直接返回区域中陆地数,因为若矩阵全0,则结果应该为1(题目说可改1次0->1)
for循环遍历四周时需要用新变量来表示四周坐标,不能直接修改原坐标,因为递归返回上一层时需要用到本层的坐标
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
var ds = [4][2]int{{1, 0}, {0, 1}, {-1, 0}, {0, -1}}
var mark int
var area int
func largestIsland(grid [][]int) int {
res := 0
mark = 2
getSize := make(map[int]int)
// 统计各个岛屿面积
for i := range grid {
for j := range grid[i] {
if grid[i][j] == 1 {
dfs(grid, i, j) // 遍历该岛屿
getSize[mark] = area // 保存岛屿面积
area = 0 // 置零
mark++ // 标记值更新
}
}
}
// 遍历0得到最大面积
for i := range grid {
for j := range grid[i] {
if grid[i][j] == 0 {
// 得到四周岛屿总面积
total := 0
accounted := make(map[int]bool)
for _, move := range ds {
x := i + move[0]
y := j + move[1]
if x < 0 || y < 0 || x == len(grid) || y == len(grid[x]) || grid[x][y] == 0 {
continue // 索引越界或遇到海洋
} else if accounted[grid[x][y]] {
continue // 该岛屿被统计过
} else {
accounted[grid[x][y]] = true // 标记该岛屿
total += getSize[grid[x][y]] // 统计该岛屿面积
}
}
res = max(res, 1+total) // 更新最大面积
}
}
}
if res == 0 {
return len(grid) * len(grid)
}
return res
}
func dfs(grid [][]int, x int, y int) {
if x < 0 || y < 0 || x == len(grid) || y == len(grid[x]) || grid[x][y] != 1 {
return // 索引越界或遇到海洋或标记过
}
grid[x][y] = mark // 标记陆地
area++ // 岛屿面积更新
for _, move := range ds {
nextX := x + move[0]
nextY := y + move[1]
dfs(grid, nextX, nextY)
}
}
|
单词接龙
127. 单词接龙 - 力扣(LeetCode)
给定两个单词 beginWord 、 endWord 和一个字典 wordList ;每次从字典中选一个单词,该单词和上一个单词只有一个字母不同,返回 从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 ;序列中第一个单词是 beginWord,序列中最后一个单词是 endWord;beginWord不在字典中,endWord在字典中;如果不存在这样的转换序列,返回 0
以示例1为例,从这个图中可以看出 hit 到 cog 的路线,不止一条,有三条,一条是最短的长度为5,两条长度为6
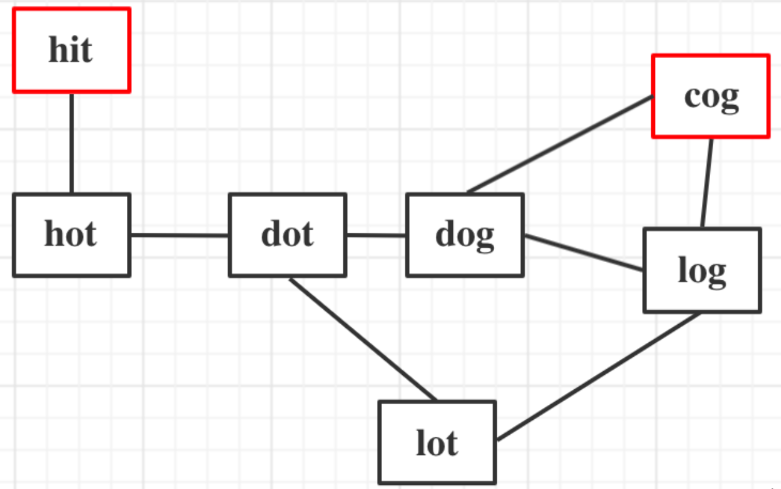
本题要解决两个问题:
- 怎样表示图中的链接:若俩单词只有一个字符不同,则有链接
- 起点和终点的最短路径长度:无向图求最短路,广搜最为合适;广搜只要搜到了终点,则一定是最短的路径,因为广搜就是以起点中心向四周扩散的搜索;本题如果用深搜会比较麻烦,要在到达终点的不同路径中选则一条最短路, 而广搜只要达到终点,一定是最短路
优化:字典可以转成map结构,查找更快一些
注意:
- 无向图需要标记节点是否走过,否则会死循环;本题即标记该单词是否用过
- 比较俩单词是否只差一个单词时,对单词中每个字母用26个字母逐个替换并检索字典中是否存在,若存在则路径长度加一,若为最终单词则返回,否则更新路径长度后入队
- go中字符串和字符互相转换:
[]rune(s)、string([]rune) ,只处理英文用byte,遍历26字母时go中用的是rune
- 遍历下一个字符前需要将上一个字符的状态复原
- 用
map对每个单词记录其路径长度,同时作为是否访问过的标志,由于是BFS,所以找到一个链接后,还会继续找本单词的其他链接,所以不能用一个变量来记录路径长度,应该单独记录每个单词的路径长度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
|
func ladderLength(beginWord string, endWord string, wordList []string) int {
// 记录到达各单词的路径长度
length := make(map[string]int)
// 初始化到达beginword的路径长度为1
length[beginWord] = 1
// 队列BFS
queue := make([]string, 0)
// 初始化beginword入队
queue = append(queue, beginWord)
// wordList转换为字典存储
wordMap := make(map[string]int)
for i, v := range wordList {
wordMap[v] = i
}
// BFS
for len(queue) != 0 {
// 取队首
word := queue[0]
queue = queue[1:]
// 逐个位置替换
for i := 0; i < len(word); i++ {
// 将不可变字符串转化为字符切片
wordSlice := []rune(word)
// 26个字母逐个试
for j := 'a'; j <= 'z'; j++ {
// 替换字符
wordSlice[i] = j
// 判断字典中是否有该单词
if _, ok := wordMap[string(wordSlice)]; ok {
// 判断该单词是否未被遍历使用过
if _, ok := length[string(wordSlice)]; !ok {
// 判断是否到达最终单词
if string(wordSlice) == endWord {
return length[word] + 1
}
// 记录到达该单词的路径长度(在替换前单词路径长度基础上加一)
length[string(wordSlice)] = length[word] + 1
// 该单词入队
queue = append(queue, string(wordSlice))
}
}
}
}
}
return 0
}
// 写法二
func ladderLength(beginWord string, endWord string, wordList []string) int {
// BFS遍历
queue := []string{beginWord}
mp := map[string]int{}
mp[beginWord] = 1
for len(queue) != 0 {
cur := queue[0]
queue = queue[1:]
// 判是否已到终点
if cur == endWord {
return mp[cur]
}
// 遍历字典中所有单词
for _, word := range wordList {
// 判字典中该单词是否已遍历过或与当前单词一致
if _, ok := mp[word]; ok || cur == word {
continue
}
// 判是否相差一个字符
if isValid(cur, word) {
mp[word] = mp[cur] + 1
queue = append(queue, word)
}
}
}
return 0
}
func isValid(str1, str2 string) bool {
cnt := 0
for i := range str1 {
if str1[i] != str2[i] {
cnt++
}
}
return cnt == 1
}
|
钥匙和房间
841. 钥匙和房间 - 力扣(LeetCode)
给定一个二维数组,第一维表示房间,第二维表示房间中的钥匙;0号房间一定是打开的,进入房间必须要钥匙,可以通过进入房间获得其他房间的钥匙;若能够进入所有房间则返回true,否则返回false
用一个数组记录所有房间的可否进入状态,同时也作为是否入过队的标志;BFS遍历给定二维数组,获得新钥匙就更新房间的可进入状态;最后遍历所有房间的可进入状态,若有房间无法进入则返回false,否则返回true
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
func canVisitAllRooms(rooms [][]int) bool {
accessible := make([]bool, len(rooms))
accessible[0] = true // 0号房间可进入
queue := make([][]int, 0) // 定义队列
queue = append(queue, rooms[0]) // 0号房入队
for len(queue) != 0 {
room := queue[0] // 取队首
queue = queue[1:] // 出队
for _, key := range room { // 遍历本房间中钥匙
if !accessible[key] { // 此房间未入过队
accessible[key] = true // 更新可进入状态
queue = append(queue, rooms[key]) // 新房入队
}
}
}
for i := range accessible {
if !accessible[i] {
return false // 有房间无法进入
}
}
return true
}
|
BFS优化:队列用一维数组保存房间下标
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
// 写法一
func canVisitAllRooms(rooms [][]int) bool {
accessible := make([]bool, len(rooms))
accessible[0] = true // 0号房间可进入
queue := make([]int, 0) // 定义队列
queue = append(queue, 0) // 0号房入队
for len(queue) != 0 {
idx := queue[0] // 取队首
queue = queue[1:] // 出队
for _, key := range rooms[idx] { // 遍历本房间中钥匙
if !accessible[key] { // 此房间未入过队
accessible[key] = true // 更新可进入状态
queue = append(queue, key) // 新房入队
}
}
}
for i := range accessible {
if !accessible[i] {
return false // 有房间无法进入
}
}
return true
}
// 写法二
func canVisitAllRooms(rooms [][]int) bool {
mp := make([]bool, len(rooms))
mp[0] = true
queue := []int{0}
for len(queue) != 0 {
for _, v := range rooms[queue[0]] {
if !mp[v] {
mp[v] = true
queue = append(queue, v)
}
}
queue = queue[1:]
}
for _, v := range mp {
if !v {
return false
}
}
return true
}
|
岛屿的周长
463. 岛屿的周长 - 力扣(LeetCode)
给定一个二维数组,表示一块区域;元素由0和1组成,1代表陆地,0代表海洋;若陆地被海洋包裹,则说明是岛屿;假设该区域四条边外是海洋;被海洋包裹的多块水平或垂直相连陆地看作一个岛屿;该区域中恰好有一个岛屿,求该岛屿的周长
遍历区域,每遇到一个陆地,岛屿周长就加四;查看该陆地的四周,每有一个岛屿,则周长减一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
func islandPerimeter(grid [][]int) int {
res := 0
for i := range grid {
for j := range grid[i] {
if grid[i][j] == 1 { // 遇到陆地
res += 4
if j != len(grid[0])-1 && grid[i][j+1] == 1 {res -= 1} // 不是最后一列且右有陆地
if i != len(grid)-1 && grid[i+1][j] == 1 {res -= 1} // 不是最后一排且下有陆地
if i != 0 && grid[i-1][j] == 1 {res -= 1} // 不是第一排且上有陆地
if j != 0 && grid[i][j-1] == 1 {res -= 1} // 不是第一列且左有陆地
}
}
}
return res
}
|
寻找图中是否存在路径
1971. 寻找图中是否存在路径 - 力扣(LeetCode)
给定整数 n表示节点总数、二维数组 edges 表示边、source 和 destination表示起点和终点,如果从 source 到 destination 存在 有效路径 ,则返回 true,否则返回 false
本题判断起点和终点是否连通,也就是判断是否在一个集合里,可以用并查集来判断
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
var father []int
func validPath(n int, edges [][]int, source int, destination int) bool {
father = make([]int, n)
initial(n)
for i := range edges {
join(edges[i][0], edges[i][1])
}
return isSame(source, destination)
}
// 并查集初始化
func initial(n int) {
for i := 0; i < n; i++ {
father[i] = i
}
}
// 并查集里寻根
func find(u int) int {
if father[u] == u {
return u
}
father[u] = find(father[u])
return father[u]
}
// 判断a和b是否找到同一个根
func isSame(a int, b int) bool {
a = find(a)
b = find(b)
return a == b
}
// 边a->b加入并差集
func join(a int, b int) {
a = find(a)
b = find(b)
if a == b {
return // 同根说明已经在一个集合里
}
father[a] = b
}
|
BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
func validPath(n int, edges [][]int, source int, destination int) bool {
// BFS
if source == destination {
return true
}
edgeMp := map[int][]int{}
for _, edge := range edges {
edgeMp[edge[0]] = append(edgeMp[edge[0]], edge[1])
edgeMp[edge[1]] = append(edgeMp[edge[1]], edge[0])
}
mp := map[int]bool{}
mp[source] = true
queue := []int{source}
for len(queue) != 0 {
cur := queue[0]
queue = queue[1:]
for _, v := range edgeMp[cur] {
if !mp[v] {
if v == destination{
return true
}
mp[v] = true
queue = append(queue, v)
}
}
}
return false
}
|
冗余连接
684. 冗余连接 - 力扣(LeetCode)
给定一个二维数组表示图中的边;要求去掉一条边,使图变为树(只有一个根节点);返回该边,若有多个答案,返回二维数组中的最后一条边
思路:遍历给定边,在将边加入并查集的过程中,若发现边的俩节点同根,说明该边加入后一定会形成环,返回该边即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
var father []int
var n int
func findRedundantConnection(edges [][]int) []int {
n = len(edges)
father = make([]int, n+1)
initial()
for i := 0; i < n; i++ {
if isSame(edges[i][0], edges[i][1]) {
return edges[i]
}
join(edges[i][0], edges[i][1])
}
return []int{}
}
func initial() {
for i := 0; i <= n; i++ {
father[i] = i
}
}
func isSame(a int, b int) bool {
a = find(a)
b = find(b)
return a == b
}
func find(u int) int {
if father[u] == u {
return u
}
father[u] = find(father[u])
return father[u]
}
func join(a int, b int) {
a = find(a)
b = find(b)
if a == b {
return
}
father[a] = b
}
|
冗余连接 II
685. 冗余连接 II - 力扣(LeetCode)
给定一个二维数组表示图中的有向边;要求去掉一条边(只有一个根节点),使图变为树;返回该边,若有多个答案,返回二维数组中的最后一条边
由于是有向边,所以需要考虑到边的方向,可以将删除边的情况分为两种,一种是有入度为2的节点,另一种是没有入度为2的节点
- 若有入度为2的节点,则需要在两条边中选择一条删除,且删除二维数组中后面的那一条
- 若无入度为2的节点,则说明仅存在一个有向环,这时和上一题一样只需要找出加入一条边,一旦该边加入即成环,返回该边即可
思路:
- 第一遍遍历各个边,统计每个节点的入度,节点值作为索引,度数作为值
- 第二遍遍历各个边,一旦发现该边指向的节点入度为2,则将该边记录;若有入度为2的节点,一定会统计出两条边
- 若第二遍遍历中能统计到两条边,则先看删掉第二条边(数组中靠后)后能否构成树,若可以则返回该边,否则返回第一条边
- 初始化并查集;将各个边加入并查集;在加入前判断,若是要删除的边则不加入,若构建树的过程中会成环则说明不能成树返回
false
- 若第二遍遍历中没有统计到两条边,说明只存在一个有向环,则找到构成环的边返回即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
|
var father []int
var n int
func findRedundantDirectedConnection(edges [][]int) []int {
inDegree := make([]int, len(edges)+1) // 记录各节点的入度
for i := range edges {
inDegree[edges[i][1]] += 1
}
twoDegree := make([]int, 0) // 记录入度为2的节点的两条边的索引
for i := range edges {
if inDegree[edges[i][1]] == 2 {
twoDegree = append(twoDegree, i) // 找到入度为2的节点的一条边
}
}
if len(twoDegree) != 0 {
if isTreeAfterRemoveEdge(edges, twoDegree[1]) {
return edges[twoDegree[1]] // 去掉数组中靠后的该边能构成树
}
return edges[twoDegree[0]] // 去掉数组中靠前的该边能构成树
}
return getRemoveEdge(edges)
}
// isTreeAfterRemoveEdge 判断删除一条边之后能否成树
func isTreeAfterRemoveEdge(edges [][]int, deleteEdgeIdx int) bool {
n = len(edges)
father = make([]int, n+1)
initial()
for i := range edges {
if i == deleteEdgeIdx {
continue // 不添加要删除的边
}
if isSame(edges[i][0], edges[i][1]) {
return false // 该边加入会成环说明不能成树
}
join(edges[i][0], edges[i][1]) // 加入并查集
}
return true
}
// getRemoveEdge 找到加入后会成环的边
func getRemoveEdge(edges [][]int) []int {
n = len(edges)
father = make([]int, n+1)
initial()
for i := range edges {
if isSame(edges[i][0], edges[i][1]) {
return edges[i] // 找到加入后会成环的边
}
join(edges[i][0], edges[i][1]) // 加入并查集
}
return []int{}
}
// 并查集
func initial() {
for i := 0; i <= n; i++ {
father[i] = i
}
}
func isSame(a int, b int) bool {
a = find(a)
b = find(b)
return a == b
}
func find(u int) int {
if father[u] == u {
return u
}
father[u] = find(father[u])
return father[u]
}
func join(a int, b int) {
a = find(a)
b = find(b)
if a == b {
return
}
father[a] = b
}
|
最小生成树⚫
卡码网:53. 寻宝
给定所有点和边的权值,求把所有点联通的最小总权值
1、prim算法
prim算法:从节点的角度,采用贪心的策略,每次寻找距离最小生成树最近的节点,找到后将其加入到最小生成树中
最小生成树是所有节点的最小连通子图, 即:以最小的成本(边的权值)将图中所有节点链接到一起
- 选距离生成树最近的节点
- 将最近的节点加入生成树
- 更新非生成树节点到生成树的距离(即更新
minDist数组)
minDist数组:记录每一个节点距离最小生成树的最近距离
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
|
package main
import (
"fmt"
"math"
)
func main() {
// v是节点个数,e是边个数
var v, e int
fmt.Scan(&v, &e)
// grid邻接矩阵保存图,权值初始化为10001,代表不相连
grid := make([][]int, v+1)
for i := range grid {
grid[i] = make([]int, v+1)
for j := range grid[i] {
grid[i][j] = 10001
}
}
// 填充grid
var x, y, k int
for ; e > 0; e-- {
fmt.Scan(&x, &y, &k)
grid[x][y] = k
grid[y][x] = k
}
// Prim算法
// 初始化minDist为10001
minDist := make([]int, v+1)
for i := range minDist {
minDist[i] = 10001
}
// 记录节点是否在最小生成树中
isInTree := make([]bool, v+1)
// 从节点1开始加入minDist
minDist[1] = 0
// 遍历节点1~v-1
for i := 1; i < v; i++ {
// 初始化最近节点为-1,最近距离为最大整型
cur := -1
minVal := math.MaxInt32
// 1. 遍历minDist找到离树的最近节点
for j := 1; j <= v; j++ {
// 判断节点是否不在树中且小于目前记录的最近距离
if !isInTree[j] && minDist[j] < minVal {
// 更新最近距离和节点
minVal = minDist[j]
cur = j
}
}
// 2. 最近节点加入树
isInTree[cur] = true
// 3. 遍历节点,更新非树中各节点到树的最近距离
for j := 1; j <= v; j++ {
// 判断是否非树中节点且离刚新入树的节点距离小于minDist记录的距离
if !isInTree[j] && grid[cur][j] < minDist[j] {
// 更新minDist
minDist[j] = grid[cur][j]
// 记录边
// parent[j] = cur
}
}
}
// 计算最小生成树的总权重
result := 0
// 遍历节点2~v
for i := 2; i <= v; i++ {
result += minDist[i]
}
fmt.Println(result)
}
|
2、Kruskal算法
Kruskal算法:从边的角度,采用贪心的策略,每次寻找权值最小的边,找到后将其加入到最小生成树中
- 将边按权值排序,优先选最小的边加入到生成树里
- 若该边首尾的两个节点在一个集合,则说明连上这条边图中会出现环
- 若该边首尾的两个节点不在同一个集合,则将该边加入到最小生成树,并把两个节点加入同一个集合
判断两个节点是否在同一个集合——并查集
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
|
package main
import (
"fmt"
"sort"
)
// 边结构体,包含边的两个端点和边的权值
type Edge struct {
From int
To int
Cost int
}
// 并查集结构体
type UnionFind struct {
parent []int
}
// 初始化并查集
func NewUnionFind(size int) *UnionFind {
parent := make([]int, size)
for i := range parent {
parent[i] = i
}
return &UnionFind{parent}
}
// 查找根节点
func (uf *UnionFind) Find(x int) int {
if uf.parent[x] != x {
uf.parent[x] = uf.Find(uf.parent[x]) // 路径压缩
}
return uf.parent[x]
}
// 加入集合
func (uf *UnionFind) Union(x, y int) {
rootX := uf.Find(x)
rootY := uf.Find(y)
if rootX != rootY {
uf.parent[rootY] = rootX
}
}
func main() {
// v是节点数,e是边数
var v, e int
fmt.Scan(&v, &e)
// 获取各个边
edges := make([]Edge, e)
for i := 0; i < e; i++ {
var v1, v2, val int
fmt.Scan(&v1, &v2, &val)
edges[i] = Edge{v1, v2, val}
}
// 按边的权值从小到大排序
sort.Slice(edges, func(i, j int) bool {
return edges[i].Cost < edges[j].Cost
})
// 初始化并查集
uf := NewUnionFind(v + 1)
result := 0
// 遍历边
for _, edge := range edges {
// 判断两个端点是否不在同一个集合中
if uf.Find(edge.From) != uf.Find(edge.To) {
// 计入结果集
result += edge.Cost
// 加入生成树中(入集)
uf.Union(edge.From, edge.To)
// 保存最小生成树的边
// res_edge = append(res_edge, edge)
}
}
fmt.Println(result)
}
|
总结:
在稀疏图中,用Kruskal更优; 在稠密图中,用prim算法更优。
边数量较少为稀疏图,接近或等于完全图(所有节点皆相连)为稠密图
Prim算法 时间复杂度为 $O(n^2)$,其中n为节点数量,它的运行效率和图中边无关,适用稠密图;Kruskal算法 时间复杂度 为 $O(nlogn)$,其中n为边的数量,适用稀疏图
拓扑排序⚫
卡码网:117. 软件构建
给定所有点和边,边表示依赖关系,判断能否按照依赖关系访问所有点
拓扑排序:给出一个有向图,把这个有向图转成线性的排序
由于拓扑排序会检测有向图是否有环,有环是不能做线性排序的,所以拓扑排序也是图论中判断有向无环图的常用方法
拓扑排序的过程,其实就两步:
- 找到入度为0 的节点,加入结果集
- 将该节点从图中移除
循环以上两步,直 所有节点都在图中被移除了
结果集的顺序,就是我们想要的拓扑排序顺序 (结果集里顺序可能不唯一)
若结果集元素个数不等于图中节点个数,则说明图中一定有环,因为找不到入度为0的节点入集
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
package main
import (
"fmt"
)
func main() {
// n个点,m个依赖关系,t依赖s
var n, m, s, t int
fmt.Scan(&n, &m)
// 记录每个文件的入度
inDegree := make([]int, n)
// 记录文件依赖关系
umap := make(map[int][]int)
result := make([]int, 0)
for i := 0; i < m; i++ {
fmt.Scan(&s, &t)
// t的入度加一
inDegree[t]++
// 记录s->t
umap[s] = append(umap[s], t)
}
queue := make([]int, 0)
// 遍历节点入度
for i := 0; i < n; i++ {
if inDegree[i] == 0 {
// 入度为0的节点作为开头加入队列
queue = append(queue, i)
}
}
for len(queue) > 0 {
// 从队列中取出当前入度为0的点
cur := queue[0]
queue = queue[1:]
result = append(result, cur)
// 获取cur指向的点
files := umap[cur]
// 遍历cur指向的点
for _, f := range files {
// cur的指向的点入度-1
inDegree[f]--
// 判断该点入度是否为0
if inDegree[f] == 0 {
// 入度为0入队
queue = append(queue, f)
}
}
}
// 判断结果集元素个数是否等于总节点数
if len(result) == n {
// 顺序打印拓扑排序序列
for i := 0; i < n-1; i++ {
fmt.Print(result[i], " ")
}
fmt.Println(result[n-1])
} else {
// 不是有向无环图,无法排序
fmt.Println(-1)
}
}
|
Dijkstra⚫
卡码网:47. 参加科学大会
给出一个有向图,一个起点,一个终点,问起点到终点的最短路径
- 选离源点最近且未被访问过的节点
- 标记该最近节点被访问
- 更新非访问节点到源点的距离(即更新minDist数组)
minDist数组:记录每个节点到源点的最短距离
朴素版
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
|
package main
import (
"fmt"
"math"
)
func main() {
// n个节点m条边,p1->p2权值val
var n, m, p1, p2, val int
fmt.Scan(&n, &m)
// 初始化邻接矩阵,用于存储边的权重
grid := make([][]int, n+1)
for i := range grid {
grid[i] = make([]int, n+1)
for j := range grid[i] {
// 使用math.MaxInt32表示两点间无边
grid[i][j] = math.MaxInt32
}
}
// 读入边信息并构建邻接矩阵
for i := 0; i < m; i++ {
fmt.Scan(&p1, &p2, &val)
grid[p1][p2] = val
}
// 起点为节点1终点为节点n
start := 1
end := n
// 存储从源点到每个节点的最短距离
minDist := make([]int, n+1)
for i := range minDist {
// 初始化为无穷大
minDist[i] = math.MaxInt32
}
// 起始点到自身的距离为0
minDist[start] = 0
// 记录点是否被访问过
visited := make([]bool, n+1)
// 遍历节点1-n
for i := 1; i <= n; i++ {
minVal := math.MaxInt32
cur := 1
// 遍历minDist选取距离源点最近且未访问过的节点
for v := 1; v <= n; v++ {
if !visited[v] && minDist[v] < minVal {
minVal = minDist[v]
cur = v
}
}
// 标记该节点已被访问
visited[cur] = true
// 更新非访问节点到源点的距离(即更新minDist数组)
for v := 1; v <= n; v++ {
if !visited[v] && grid[cur][v] != math.MaxInt32 && minDist[cur]+grid[cur][v] < minDist[v] {
minDist[v] = minDist[cur] + grid[cur][v]
// 记录边
// parent[v] = cur;
}
}
}
if minDist[end] == math.MaxInt32 {
// 不能到达终点
fmt.Println(-1)
} else {
// 到达终点最短路径
fmt.Println(minDist[end])
}
}
|
- 时间复杂度:$O(n^2)$
- 空间复杂度:$O(n^2)$
堆优化版:邻接表(数组+链表)存储边,适用于稀疏图
在处理三部曲里的第一步(选离源点最近且未被访问过的节点)的时候 ,可以不用去遍历所有节点,直接把边(带权值)加入到小顶堆(利用堆来自动排序),每次从堆顶里取出边自然就是距离源点最近的节点所在的边,这样就不需要两层for循环来寻找最近的节点了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
|
package main
import (
"container/heap"
"fmt"
"math"
)
// 定义边的结构体
type Edge struct {
to int
val int
}
func main() {
var n, m, p1, p2, val int
fmt.Scan(&n, &m)
// 初始化邻接表
grid := make([][]Edge, n+1)
// 读入边信息并构建邻接表
for i := 0; i < m; i++ {
fmt.Scan(&p1, &p2, &val)
grid[p1] = append(grid[p1], Edge{p2, val})
}
start := 1
end := n
// 存储从源点到每个节点的最短距离
minDist := make([]int, n+1)
for i := range minDist {
minDist[i] = math.MaxInt32 // 初始化为无穷大
}
minDist[start] = 0 // 起始点到自身的距离为0
// 使用优先队列实现最小堆
pq := make(PriorityQueue, 0)
heap.Init(&pq)
heap.Push(&pq, &Item{value: start, priority: 0})
// 记录顶点是否被访问过
visited := make([]bool, n+1)
for pq.Len() > 0 {
// 从优先队列中取出当前距离起点最近的节点
item := heap.Pop(&pq).(*Item)
u := item.value
if visited[u] {
continue
}
visited[u] = true
// 更新与当前节点相邻的节点的最短距离
for _, edge := range grid[u] {
v := edge.to
w := edge.val
if !visited[v] && minDist[u]+w < minDist[v] {
minDist[v] = minDist[u] + w
heap.Push(&pq, &Item{value: v, priority: minDist[v]})
}
}
}
// 输出结果
if minDist[end] == math.MaxInt32 {
fmt.Println(-1) // 不能到达终点
} else {
fmt.Println(minDist[end]) // 到达终点最短路径
}
}
// 优先队列实现(最小堆)
type Item struct {
value int // 节点编号
priority int // 源点到该节点的距离
}
type PriorityQueue []*Item
func (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool {
return pq[i].priority < pq[j].priority
}
func (pq PriorityQueue) Swap(i, j int) {
pq[i], pq[j] = pq[j], pq[i]
}
func (pq *PriorityQueue) Push(x interface{}) {
item := x.(*Item)
*pq = append(*pq, item)
}
func (pq *PriorityQueue) Pop() interface{} {
old := *pq
n := len(old)
item := old[n-1]
*pq = old[0 : n-1]
return item
}
|
- 时间复杂度:$O(ElogE)$, $E$ 为边的数量
- 空间复杂度:$O(N + E)$, $N$ 为节点的数量
Bellman_ford⚫
卡码网:94. 城市间货物运输 I
给出一个有向图,一个起点,一个终点,问起点到终点的最短路径,边的权值有负数,但不存在任何负权回路。
负权回路是指一系列道路的总权值为负,这样的回路使得通过反复经过回路中的道路,理论上可以无限地减少总成本或无限地增加总收益。
minDist数组:表示起点到各个节点的最短距离,例如minDist[3] = 5表示起点到达节点3的最小距离为5
Bellman_ford:对所有边松弛n-1次,得出起点到终点的最短路径
- 松弛:动态规划,假设
minDist[B] 表示到达B节点的最小权值,minDist[B] = min(minDist[A] + value, minDist[B])
- 状态一:
minDist[A] + value 可以推出 minDist[B]
- 状态二:
minDist[B]本身就有权值 (可能是C->B的权值)
- 对所有边松弛一次,相当于计算起点到与起点一条边相连的节点的最短距离
- 对所有边松弛
n-1次,就一定能得到起点到终点的最短距离
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
package main
import (
"fmt"
"math"
)
func main() {
var n, m, p1, p2, val int
fmt.Scan(&n, &m)
// 创建邻接表
grid := make([][]int, 0)
// 读入边信息并构建邻接表
for i := 0; i < m; i++ {
fmt.Scan(&p1, &p2, &val)
grid = append(grid, []int{p1, p2, val})
}
start := 1
end := n
// 存储从源点到每个节点的最短距离
minDist := make([]int, n+1)
for i := range minDist {
// 初始化为无穷大
minDist[i] = math.MaxInt32
}
// 起始点到自身的距离为0
minDist[start] = 0
// 进行 n-1 次松弛操作
for i := 1; i < n; i++ {
for _, side := range grid {
from := side[0]
to := side[1]
price := side[2]
if minDist[from] != math.MaxInt32 && minDist[to] > minDist[from]+price {
minDist[to] = minDist[from] + price
}
}
}
// 输出结果
if minDist[end] == math.MaxInt32 {
// 不能到达终点
fmt.Println("unconnected")
} else {
// 到达终点最短路径
fmt.Println(minDist[end])
}
}
|
- 时间复杂度: $O(N*E)$ ,$N$为节点数量,$E$为图中边的数量
- 空间复杂度: $O(N)$ ,即
minDist数组所开辟的空间
Bellman_ford 队列优化算法⚫
卡码网:94. 城市间货物运输 I
给出一个有向图,一个起点,一个终点,问起点到终点的最短路径,边的权值有负数,但不存在任何负权回路。
负权回路是指一系列道路的总权值为负,这样的回路使得通过反复经过回路中的道路,理论上可以无限地减少总成本或无限地增加总收益。
Bellman_ford队列优化算法 ,也叫SPFA算法(Shortest Path Faster Algorithm)。
SPFA的称呼来自 1994年西南交通大学段凡丁的论文,其实Bellman_ford提出后不久 (20世纪50年代末期) 就有队列优化的版本,国际上不承认这个算法是是国内提出的。 所以国际上一般称呼该算法为Bellman_ford队列优化算法(Queue improved Bellman-Ford)
Bellman_ford算法每次都是对所有边进行松弛,其实是多做了一些无用功。只需要对上一次松弛的时候更新过的节点作为出发节点所连接的边进行松弛就够了。基于以上思路,用队列来记录上次松弛的时候更新过的节点;在加入队列的过程可以有一个优化:用visited数组记录已经在队列里的元素,已经在队列的元素不用重复加入
依然使用minDist数组表示起点到各个节点的最短距离,例如minDist[3] = 5表示起点到节点3的最小距离为5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
|
package main
import (
"container/list"
"fmt"
"math"
)
// Edge 结构体表示图中的一条边
type Edge struct {
to int // 目标节点
val int // 边的权重
}
func main() {
var n, m, p1, p2, val int
fmt.Scan(&n, &m)
// 创建邻接表
grid := make([]*list.List, n+1)
for i := range grid {
grid[i] = list.New()
}
// 读取边信息并构建邻接表
for i := 0; i < m; i++ {
fmt.Scan(&p1, &p2, &val)
grid[p1].PushBack(Edge{to: p2, val: val})
}
start := 1
end := n
// 存储从源点到每个节点的最短距离
minDist := make([]int, n+1)
for i := range minDist {
// 初始化为无穷大
minDist[i] = math.MaxInt32
}
minDist[start] = 0
que := list.New()
que.PushBack(start)
// 记录已经在队列里的元素
isInQueue := make([]bool, n+1)
isInQueue[start] = true
// 遍历队列
for que.Len() > 0 {
front := que.Front()
node := front.Value.(int)
que.Remove(front)
// 从队列里取出的时候,要取消标记,只保证已经在队列里的元素不用重复加入
isInQueue[node] = false
for e := grid[node].Front(); e != nil; e = e.Next() {
edge := e.Value.(Edge)
to := edge.to
value := edge.val
if minDist[to] > minDist[node]+value {
// 开始松弛
minDist[to] = minDist[node] + value
// 已经在队列里的元素不用重复添加
if !isInQueue[to] {
que.PushBack(to)
isInQueue[to] = true
}
}
}
}
// 输出结果
if minDist[end] == math.MaxInt32 {
// 不能到达终点
fmt.Println("unconnected")
} else {
// 到达终点的最短路径
fmt.Println(minDist[end])
}
}
|
- 时间复杂度:最坏的情况下是 $O(N * E)$,一般情况下为$O(K * N)$
SPFA(队列优化版Bellman_ford)在理论上时间复杂度更胜一筹,但实际上,也要看图的稠密程度,如果图很大且非常稠密的情况下,虽然SPFA的时间复杂度接近Bellman_ford,但SPFA实际时间消耗可能更多
bellman_ford 判断负权回路⚫
卡码网:95. 城市间货物运输 II
给出一个有向图,一个起点,一个终点,问起点到终点的最短路径,边的权值有负数,图中可能存在负权回路。
负权回路是指一系列道路的总权值为负,这样的回路使得通过反复经过回路中的道路,理论上可以无限地减少总成本或无限地增加总收益,算法需要能检测出这种特殊情况
在有负权回路的情况下,一直都会有更短的最短路,所以松弛第n次后,minDist数组也会发生改变。所有判断图中是否有负权回路的核心思路就是在松弛n-1次的基础上,再多松弛一次,看minDist数组是否发生变化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
package main
import (
"fmt"
"math"
)
func main() {
var n, m, p1, p2, val int
fmt.Scan(&n, &m)
var grid [][3]int
for i := 0; i < m; i++ {
fmt.Scan(&p1, &p2, &val)
// p1 指向 p2,权值为 val
grid = append(grid, [3]int{p1, p2, val})
}
// 起点
start := 1
// 终点
end := n
minDist := make([]int, n+1)
for i := range minDist {
// 初始化为无穷大
minDist[i] = math.MaxInt32
}
minDist[start] = 0
flag := false
// 松弛 n 次,最后一次判断负权回路
for i := 1; i <= n; i++ {
for _, side := range grid {
from := side[0]
to := side[1]
price := side[2]
if i < n {
if minDist[from] != math.MaxInt32 && minDist[to] > minDist[from]+price {
minDist[to] = minDist[from] + price
}
} else {
// 多加一次松弛判断负权回路
if minDist[from] != math.MaxInt32 && minDist[to] > minDist[from]+price {
flag = true
}
}
}
}
if flag {
fmt.Println("circle")
} else if minDist[end] == math.MaxInt32 {
fmt.Println("unconnected")
} else {
fmt.Println(minDist[end])
}
}
|
- 时间复杂度: $O(N * E)$ , $N$为节点数量,$E$为图中边的数量
- 空间复杂度: $O(N)$,即
minDist数组所开辟的空间
bellman_ford 单源有限最短路⚪
卡码网:96. 城市间货物运输 III
787. K 站中转内最便宜的航班
给出一个有向图,一个起点,一个终点,一个整数k,问在最多经过 k 个点的条件下,起点到终点的最短路径,边的权值有负数,图中可能存在负权回路。
负权回路是指一系列道路的总权值为负,这样的回路使得通过反复经过回路中的道路,理论上可以无限地减少总成本或无限地增加总收益,算法需要能检测出这种特殊情况
本题是单源有限最短路问题,最多经过k个点, 那么就是k + 1条边相连的节点
对所有边松弛一次,相当于计算起点到与起点一条边相连的节点的最短距离
对所有边松弛k + 1次,就得到从起点到与起点k + 1条边相连的节点的最短距离
每次计算 minDist 时候,要基于对所有边上一次松弛的minDist数值才行,所以要记录上一次松弛的minDist
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
|
// 核心代码
func findCheapestPrice(n int, flights [][]int, src int, dst int, k int) int {
// 单源有限最短路:SPFA
// 从src到i的最近距离
minDist := make([]int, n)
// 初始化minDist
for i := range minDist {
minDist[i] = math.MaxInt32
}
// 初始化src到src距离为0
minDist[src] = 0
// 对所有边松弛k+1次
for i := 1; i <= k+1; i++ {
// 保存上一次松弛结果
minDistTemp := make([]int, len(minDist))
copy(minDistTemp, minDist)
// 对所有边松弛一次
for _, side := range flights {
from, to, price := side[0], side[1], side[2]
// 判src到from是否可达
if minDistTemp[from] != math.MaxInt32 {
// 动规
// min(起点到当前点的距离, 上一次松弛后src到from的距离 + from到to距离)
minDist[to] = min(minDist[to], minDistTemp[from]+price)
}
}
}
if minDist[dst] != math.MaxInt32 {
return minDist[dst]
}
return -1
}
// ACM模式
package main
import (
"bufio"
"fmt"
"os"
"strconv"
)
func main() {
scanner := bufio.NewScanner(os.Stdin)
scanner.Split(bufio.ScanWords)
n, m := readTwoInts(scanner)
grid := make([][]int, m)
for i := 0; i < m; i++ {
p1, p2, val := readThreeInts(scanner)
grid[i] = []int{p1, p2, val}
}
src, dst, k := readThreeInts(scanner)
minDist := make([]int, n+1)
// 用来记录上一次遍历的结果
minDistCopy := make([]int, n+1)
for i := range minDist {
minDist[i] = int(^uint(0) >> 1) // Equivalent of INT_MAX in Go
// 获取上一次计算的结果
minDistCopy[i] = minDist[i]
}
minDist[src] = 0
// 对所有边松弛k+1次
for i := 1; i <= k+1; i++ {
copy(minDistCopy, minDist)
// 对所有边松弛一次
for _, side := range grid {
from, to, price := side[0], side[1], side[2]
// 注意使用 minDistCopy 来计算 minDist
// 判是否上一次松弛后,起点到from点非不可达
if minDistCopy[from] != int(^uint(0)>>1) {
// min(起点到当前点的距离, 上一次松弛后起点到from点的距离+from点到to点距离)
minDist[to] = min(minDist[to], minDistCopy[from]+price)
}
}
}
if minDist[dst] == int(^uint(0)>>1) {
// 不能到达终点
fmt.Println("unreachable")
} else {
// 到达终点最短路径
fmt.Println(minDist[dst])
}
}
func readTwoInts(scanner *bufio.Scanner) (int, int) {
scanner.Scan()
text := scanner.Text()
a, _ := strconv.Atoi(text)
scanner.Scan()
text = scanner.Text()
b, _ := strconv.Atoi(text)
return a, b
}
func readThreeInts(scanner *bufio.Scanner) (int, int, int) {
a, b := readTwoInts(scanner)
scanner.Scan()
text := scanner.Text()
c, _ := strconv.Atoi(text)
return a, b, c
}
|
- 时间复杂度: $O(K * E)$ ,$K$为至多经过$K$个节点,$E$为图中边的数量
- 空间复杂度: $O(N)$ ,即
minDist数组所开辟的空间
对比本题与前面讲解过的 94.城市间货物运输I 和 95.城市间货物运输II
94.城市间货物运输I,没有负权回路的,那么多松弛多少次,对结果都没有影响
- 求节点1到节点n的最短路径,松弛
n-1次就够了,松弛大于n-1次,结果也不会变
- 在对所有边进行第一次松弛的时候,如果基于本次计算的
minDist来计算minDist(相当于多做松弛了),也是对最终结果没影响
95.城市间货物运输II,判断是否有负权回路,一旦有负权回路, 对所有边松弛n-1次以后,再做松弛,minDist数值一定会变,根据这一点来判断是否有负权回路
- 只需要判断
minDist数值是否变化了就行,而minDist的数值对不对,并不关心
本题计算minDist一定要基于上次的minDist数值,其关键在于本题的两个因素:
- 本题可以有负权回路,说明只要多做松弛,结果是会变的
- 本题要求最多经过
k个节点,对松弛次数是有限制的
Floyd⚫
卡码网:97. 小明逛公园
多源最短路问题,求多个起点到多个终点的多条最短路径
Floyd 算法对边的权值正负没有要求,核心思想是动态规划
grid[i][j][k] = m:节点i到节点j,以[1...k]集合为中间节点的最短距离为m- 递推公式:分两种情况,节点
i到节点j的最短路径经过节点k、节点i到节点j的最短路径不经过节点k
grid[i][j][k] = min(grid[i][k][k-1]+grid[k][j][k-1], grid[i][j][k-1])
- 初始化:
grid[i][j][0] = val、grid[i][j][k] = max (k ≠ 0)
- 遍历顺序:三维中
i j为底平面,k为纵轴,自底向上遍历
空间优化:
-
从滚动数组的角度来看,定义一个grid[i][j][2]这么大的数组就可以,因为k只依赖于k-1的状态,那么只记录grid[i][j][1]和grid[i][j][0]就好,之后就是grid[i][j][1]和grid[i][j][0]交替滚动
-
如果本层刚计算好的grid[i][k]比上一层 (即k-1层)计算的grid[i][k]小,说明确实有i到k的更短路径,那么基于更小的grid[i][k]去计算gird[i][j]没有问题。如果 本层刚计算好的grid[i][k]比上一层 (即k-1层)计算的grid[i][k]大, 这不可能,因为这样也不会做更新grid[i][k]的操作
所以本层计算中就没必要区分,grid[i][k]和grid[k][j]是属于k - 1层的还是k层的,故递归公式可以为:
grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
|
package main
import (
"fmt"
)
func main() {
var n, m int
fmt.Scanf("%d %d", &n, &m)
grid := make([][]int, n+1)
for i := range grid {
grid[i] = make([]int, n+1)
for j := range grid[i] {
// 最大距离
grid[i][j] = 10005
}
}
for i := 0; i < m; i++ {
var p1, p2, val int
fmt.Scanf("%d %d %d", &p1, &p2, &val)
// 双向图
grid[p1][p2] = val
grid[p2][p1] = val
}
// 开始Floyd
for k := 1; k <= n; k++ {
for i := 1; i <= n; i++ {
for j := 1; j <= n; j++ {
grid[i][j] = min(grid[i][j], grid[i][k]+grid[k][j])
}
}
}
// 输出结果
var z int
fmt.Scanf("%d", &z)
for z > 0 {
z--
var start, end int
fmt.Scanf("%d %d", &start, &end)
if grid[start][end] == 10005 {
fmt.Println(-1)
} else {
fmt.Println(grid[start][end])
}
}
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
|
- 时间复杂度:$O(n^3)$
- 空间复杂度:$O(n^2)$
A star⚫
卡码网:126. 骑士的攻击
Astar是一种广搜的改良版,有的是Astar是 dijkstra 的改良版;其实只是场景不同,在搜索最短路的时候,如果是无权图(边的权值都是1) 就用广搜,代码简洁,时间效率和 dijkstra 差不多 (具体要取决于图的稠密),如果是有权图(边有不同的权值),优先考虑 dijkstra;而 Astar 关键在于启发式函数, 也就是影响广搜或者 dijkstra 从容器(队列)里取元素的优先顺序;下面介绍BFS版本的A star
对队列中的节点按权值F进行排序:F = G + H
- G:起点达目前遍历节点的距离
- H:目前遍历的节点到终点的距离
起点到终点的距离 = 起点到目前遍历节点的距离 + 目前遍历节点到终点的距离
本题的图是无权网格,在计算两点距离时通常有三种计算方式:
- 曼哈顿距离:$d = \abs{(x_1-x_2)+\abs{y_1-y_2}}$
- 欧氏距离(欧拉距离):$d = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2 )}$
- 切比雪夫距离:$d = max(\abs{x_1 - x_2}, \abs{y_1 - y_2})$
选择不同的距离计算方式也会导致 Astar算法的结果不同,本题需要采用欧拉距离才能最大程度体现点与点之间的距离
可以使用优先级队列排序,每次出队的就是F最小的节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
|
package main
import (
"container/heap"
"fmt"
)
const (
maxN = 1001
)
var moves [maxN][maxN]int
var dir = [8][2]int{
{-2, -1}, {-2, 1}, {-1, 2}, {1, 2},
{2, 1}, {2, -1}, {1, -2}, {-1, -2},
}
type Knight struct {
x, y, g, h, f int
}
type KnightHeap []Knight
func (h KnightHeap) Len() int { return len(h) }
func (h KnightHeap) Less(i, j int) bool { return h[i].f < h[j].f }
func (h KnightHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *KnightHeap) Push(x interface{}) {
*h = append(*h, x.(Knight))
}
func (h *KnightHeap) Pop() interface{} {
old := *h
n := len(old)
x := old[n-1]
*h = old[0 : n-1]
return x
}
// 欧拉距离
func heuristic(k Knight, b1, b2 int) int {
// 统一不开根号,这样可以提高精度
return (k.x-b1)*(k.x-b1) + (k.y-b2)*(k.y-b2)
}
func astar(start Knight, b1, b2 int) int {
h := &KnightHeap{}
heap.Init(h)
heap.Push(h, start)
for h.Len() > 0 {
cur := heap.Pop(h).(Knight)
if cur.x == b1 && cur.y == b2 {
return moves[b1][b2]
}
for _, d := range dir {
nextX := cur.x + d[0]
nextY := cur.y + d[1]
if nextX < 1 || nextX >= maxN || nextY < 1 || nextY >= maxN {
continue
}
if moves[nextX][nextY] == 0 {
moves[nextX][nextY] = moves[cur.x][cur.y] + 1
// 开始计算F
next := Knight{
x: nextX,
y: nextY,
g: cur.g + 5,
h: heuristic(Knight{x: nextX, y: nextY}, b1, b2),
}
next.f = next.g + next.h
heap.Push(h, next)
}
}
}
// unreachable case
return -1
}
func main() {
var n, a1, a2, b1, b2 int
fmt.Scan(&n)
for n > 0 {
fmt.Scan(&a1, &a2, &b1, &b2)
for i := range moves {
for j := range moves[i] {
moves[i][j] = 0
}
}
if a1 < 1 || a1 >= maxN || a2 < 1 || a2 >= maxN || b1 < 1 || b1 >= maxN || b2 < 1 || b2 >= maxN {
fmt.Println(-1)
n--
continue
}
start := Knight{
x: a1,
y: a2,
g: 0,
h: heuristic(Knight{x: a1, y: a2}, b1, b2),
}
start.f = start.g + start.h
result := astar(start, b1, b2)
fmt.Println(result)
n--
}
}
|
- 时间复杂度:$O(nlogn)$ ,n为节点数量。
- 空间复杂度:$O(b ^ d)$ ,d 为起点到终点的深度,b 是图中节点间的连接数量
最短路算法总结
四大最短路算法:Dijkstra、Bellman_ford、SPFA 和 Floyd
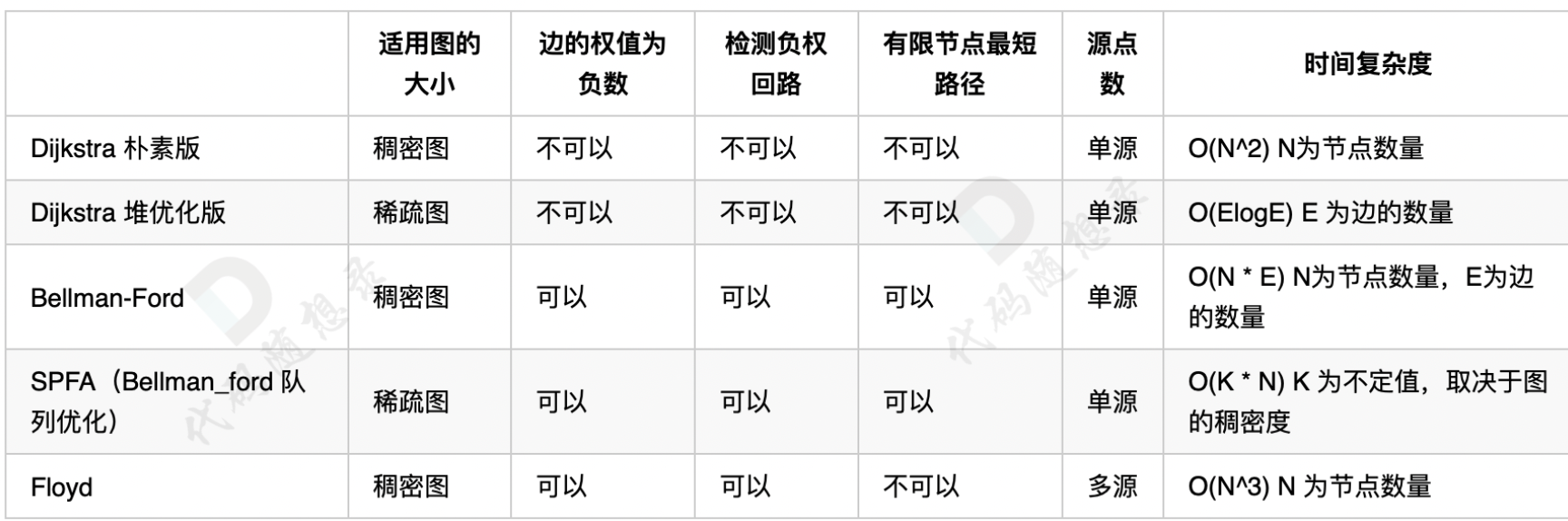
(因为A * 属于启发式搜索,和上面最短路算法并不是一类,不适合一起对比,所以没有放在一起)
- 如果遇到单源且边为正数,直接Dijkstra,至于使用朴素版还是堆优化版还是取决于图的稠密度,一般情况下,可以直接用堆优化版本
- 如果遇到单源边可为负数,直接 Bellman-Ford,同样 SPFA 还是 Bellman-Ford 取决于图的稠密度,一般情况下,直接用 SPFA
- 如果有负权回路,优先 Bellman-Ford, 如果是有限节点最短路也优先 Bellman-Ford,理由是写代码比较方便
- 如果是遇到多源点求最短路,直接 Floyd,除非源点特别少,且边都是正数,那可以多次 Dijkstra 求出最短路径,但这种情况很少,一般出现多个源点了,就用 Floyd
- A star由于其高效性,在实际工程应用中使用最为广泛,游戏开发、地图导航、数据包路由等都广泛使用 A * 算法 ,但由于其结果的不唯一性,也就是可能是次短路的特性,一般不适合作为算法题,
腐烂的橘子
994. 腐烂的橘子 - 力扣(LeetCode)
在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:值 0 代表空单元格;值 1 代表新鲜橘子;值 2 代表腐烂的橘子。每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1
思路:多源BFS
- 先遍历一边网格,统计出新鲜橘子个数,同时将烂橘子坐标入队;
- 遍历队列,每遍历一次当前队列中所有烂橘子分钟数+1,遍历时向四周探索一次若发现新鲜橘子,则传染该新鲜橘子,新鲜橘子计数-1,感染后的烂橘子坐标入队;
- 重复该过程直到队列为空,说明没有新感染的烂橘子;
- 此时判断是否还存在新鲜橘子,若存在,说明烂橘子无法感染所有新鲜橘子,返回
-1;否则说明所有橘子都已为烂橘子,此时返回经过的分钟数
注意:
- 若初始化分钟数为0,则返回经过的分钟数时需要-1,因为最后一次队中的烂橘子没有感染其他新鲜橘子,但是遍历最后一次队中的烂橘子时分钟数+1了,所以网格中没有新鲜橘子经过的最小分钟数应该-1
- 由于返回经过的分钟数-1了,所以有可能一开始网格中就没有橘子,此时分钟数为0,会返回-1,但返回-1代表网格中有新鲜橘子永远不会被感染,正确应该返回0,说明经过0分钟网格中就没有新鲜橘子了;所以在最后判断没有新鲜橘子后,需要返回经过的分钟数时需要与0比较,返回大值,保证返回经过的分钟数不会为负数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
|
// 写法一
var directions = [4][2]int{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}
func orangesRotting(grid [][]int) int {
// 统计目前的空格数和新鲜橘子数
count1 := 0
// 存储烂橘子
queue := make([][]int, 0)
// 遍历初始网格
for i := range grid {
for j := range grid[i] {
// 判断是否遇到新鲜橘子
if grid[i][j] == 1 {
count1++
} else if grid[i][j] == 2 {
// 烂橘子入队
queue = append(queue, []int{i, j})
}
}
}
minute := 0
// 遍历烂橘子队列
for len(queue) != 0 {
// 分钟数+1
minute++
// 记录本分钟的烂橘子数
cnt := len(queue)
// 遍历本分钟所有烂橘子
for i := 0; i < cnt; i++ {
// 取一个烂橘子
curX, curY := queue[0][0], queue[0][1]
queue = queue[1:]
for _, offset := range directions {
x, y := curX+offset[0], curY+offset[1]
if x >= 0 && y >= 0 && x < len(grid) && y < len(grid[0]) && grid[x][y] == 1 {
// 更新新鲜橘子数
count1--
// 烂橘子扩散
grid[x][y] = 2
// 记录烂橘子坐标
queue = append(queue, []int{x, y})
}
}
}
}
// 还有新鲜橘子
if count1 != 0 {
return -1
}
return max(minute-1, 0)
}
// 写法二
func orangesRotting(grid [][]int) int {
// BFS
queue := [][]int{}
cnt := 0
for i := range grid {
for j := range grid[i] {
if grid[i][j] == 1 {
cnt++
} else if grid[i][j] == 2 {
queue = append(queue, []int{i, j, 0})
}
}
}
if cnt == 0 {
return 0
}
dis := [4][2]int{{1, 0}, {-1, 0}, {0, 1}, {0, -1}}
for len(queue) != 0 {
curX := queue[0][0]
curY := queue[0][1]
curMinute := queue[0][2]
queue = queue[1:]
for _, offset := range dis {
nextX := curX + offset[0]
nextY := curY + offset[1]
if nextX >= 0 && nextY >= 0 && nextX < len(grid) && nextY < len(grid[0]) && grid[nextX][nextY] == 1 {
cnt--
if cnt == 0 {
return curMinute + 1
}
grid[nextX][nextY] = 2
queue = append(queue, []int{nextX, nextY, curMinute + 1})
}
}
}
return -1
}
// 写法三
func orangesRotting(grid [][]int) int {
dis := [4][2]int{{1, 0}, {-1, 0}, {0, 1}, {0, -1}}
// BFS
queue := [][]int{}
// 初始化队列:遍历矩阵将烂橘子入队
for i := range grid {
for j := range grid[i] {
if grid[i][j] == 2 {
queue = append(queue, []int{i, j})
}
}
}
res := 0
for len(queue) != 0 {
res++
cnt := len(queue)
// 遍历本分钟所有烂橘子
for i := 0; i < cnt; i++ {
cur := queue[0]
queue = queue[1:]
for _, offset := range dis {
x := cur[0] + offset[0]
y := cur[1] + offset[1]
if x >= 0 && x < len(grid) && y >= 0 && y < len(grid[0]) && grid[x][y] == 1 {
grid[x][y] = 2
queue = append(queue, []int{x, y})
}
}
}
}
// 判是否还有鲜橘子
for i := range grid {
for j := range grid[i] {
if grid[i][j] == 1 {
return -1
}
}
}
// 判res是否非0
if res != 0 {
res--
}
return res
}
|
课程表
207. 课程表 - 力扣(LeetCode)
给定一个整数表示要上的课程数,一个二维数组表示每俩课程间的依赖关系,前依赖后;判断是否能修完全部课
思路:拓扑排序;判断能否把一个 有向无环图 转成 线性的排序
- 用数组记录每个节点的入度,不需要前置节点的节点的入度为0;用哈希表记录依赖当前节点的所有节点,key:当前节点,value:依赖当前节点的所有节点
- 将入度为0的节点入队,逐个访问表示学习该课,同时将依赖该课的所有课程入度-1,若入度减为0,则入队
- 队列遍历结束后,遍历所有节点入度,判断是否仍有入度不为0的节点,若有说明有环,返回
false,否则返回true
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
func canFinish(numCourses int, prerequisites [][]int) bool {
indegree := make([]int, numCourses)
mp := make(map[int][]int)
queue := make([]int, 0)
// 遍历前置关系,统计入度和依赖关系
for _, pairs := range prerequisites {
// 统计入度
indegree[pairs[0]]++
// 记录依赖关系
mp[pairs[1]] = append(mp[pairs[1]], pairs[0])
}
// 遍历入度找出入度为0的课入队
for i, v := range indegree {
if v == 0 {
queue = append(queue, i)
}
}
// 遍历队列
for len(queue) != 0 {
// 取出一个节点表示学习该课
cur := queue[0]
queue = queue[1:]
// 判断是否有依赖当前课的课
if courses, ok := mp[cur]; ok {
// 遍历所有依赖当前课的课
for _, course := range courses {
// 更新入度
indegree[course]--
// 判断入度是否减为0
if indegree[course] == 0 {
// 0入度节点入队
queue = append(queue, course)
}
}
}
}
// 遍历入度判断是否仍有入度非0的节点
for _, v := range indegree {
if v != 0 {
return false
}
}
return true
}
|
实现 Trie (前缀树)
208. 实现 Trie (前缀树) - 力扣(LeetCode)
Trie(发音类似 “try”)或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补全和拼写检查。
要求实现 Trie 类:
Trie() 初始化前缀树对象void insert(String word) 向前缀树中插入字符串 wordboolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 falseboolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false
Trie介绍
Trie 是一颗非典型的多叉树模型,多叉好理解,即每个节点的分支数量可能为多个。
前缀树可以用 O(l) 的时间复杂度完成如下操作,其中 I 是插入字符串或查询前缀的长度
非典型是因为它和一般的多叉树不一样,尤其在节点的数据结构设计上,一般的多叉树的节点是这样的:
1
2
3
4
5
6
|
type TreeNode struct {
// 节点值
Val int
// 指向孩子节点
children []*TreeNode
}
|
而 Trie 的节点是这样的(假设只包含’a'~‘z’中的字符):
1
2
3
4
5
6
|
type TrieNode struct {
// 标记该节点是否是一个串的结束
isEnd bool
// 字母映射表
children [26]*TrieNode
}
|
TrieNode节点中并没有直接保存字符值的数据成员,但**字母映射表children**中保存了对当前节点而言下一个可能出现的所有字符的链接,因此可以通过一个父节点来获知它所有子节点的值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
type Trie struct {
isEnd bool
children [26]*Trie
}
func Constructor() Trie {
return Trie{}
}
func (this *Trie) Insert(word string) {
// 初始化指向根节点
cur := this
// 遍历要插入的字符串
for _, ch := range word {
// 判当前节点是否无指向该字符的子节点
if cur.children[ch-'a'] == nil {
// 创建该子节点并记入当前节点
cur.children[ch-'a'] = new(Trie)
}
// 指向该子节点
cur = cur.children[ch-'a']
}
// 遍历字符串结束标记当前字符为一个结尾
cur.isEnd = true
}
func (this *Trie) Search(word string) bool {
cur := this
for _, ch := range word {
// 判断是否未找到该字符
if cur.children[ch-'a'] == nil {
return false
}
cur = cur.children[ch-'a']
}
// 若当前字符是一个结尾则返回true,反之返回false
return cur.isEnd
}
func (this *Trie) StartsWith(prefix string) bool {
cur := this
for _, ch := range prefix {
if cur.children[ch-'a'] == nil {
return false
}
cur = cur.children[ch-'a']
}
return true
}
|
- 时间复杂度:O(L),L 是字符串的长度
- 空间复杂度:O(n^2),最差情况下每个字符串都不相同
搜索推荐系统
1268. 搜索推荐系统 - 力扣(LeetCode)
给定一个产品数组 products 和一个字符串 searchWord ,products 数组中每个产品都是一个字符串。设计一个推荐系统,在依次输入单词 searchWord 的每一个字母后,推荐 products 数组中前缀与 searchWord 相同的最多三个产品。如果前缀相同的可推荐产品超过三个,按字典序返回最小的三个。以二维列表的形式,返回在输入 searchWord 每个字母后相应的推荐产品的列表
思路:前缀树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
|
type Trie struct {
alpha [26]*Trie
isEnd bool
}
func suggestedProducts(products []string, searchWord string) [][]string {
trie := new(Trie)
for _, product := range products {
trie.insert(product)
}
res := [][]string{}
for i := range searchWord {
res = append(res, trie.search(searchWord[:i+1]))
}
return res
}
func (this *Trie) insert(word string) {
cur := this
for _, ch := range word {
if cur.alpha[ch-'a'] == nil {
cur.alpha[ch-'a'] = &Trie{}
}
cur = cur.alpha[ch-'a']
}
cur.isEnd = true
}
func (this *Trie) search(word string) []string {
res := []string{}
cur := this
for _, ch := range word {
if cur.alpha[ch-'a'] == nil {
return res
}
cur = cur.alpha[ch-'a']
}
path := []byte(word)
var dfs func(*Trie)
dfs = func(cur *Trie) {
if cur.isEnd {
res = append(res, string(path))
}
for i, trie := range cur.alpha {
if trie != nil {
path = append(path, byte('a'+i))
dfs(trie)
path = path[:len(path)-1]
}
}
}
dfs(cur)
if len(res) <= 3 {
return res
}
sort.Strings(res)
return res[:3]
}
// 写法二:只取三个 节省空间 但需要多判断
func (this *Trie) startWith(prefix string) []string {
cur := this
res := make([]string, 0, 3)
for _, ch := range prefix {
if cur.alph[ch-'a'] == nil {
return []string{}
}
cur = cur.alph[ch-'a']
}
path := []byte(prefix)
var dfs func(*Trie)
dfs = func(cur *Trie) {
if cur == nil {
return
}
if len(res) == 3 {
return
}
if cur.isEnd {
res = append(res, string(path))
if len(res) == 3 {
return
}
}
for i, v := range cur.alph {
path = append(path, byte('a'+i))
dfs(v)
path = path[:len(path)-1]
}
}
dfs(cur)
return res
}
|
除法求值
399. 除法求值 - 力扣(LeetCode)
给定一个变量对数组 equations 和一个实数值数组 values 作为已知条件,其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。另有一些以数组 queries 表示的问题,其中 queries[j] = [Cj, Dj] 表示第 j 个问题,请根据已知条件找出 Cj / Dj = ? 的结果作为答案。返回 所有问题的答案 。如果存在某个无法确定的答案,则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串,也需要用 -1.0 替代这个答案。
**注意:**输入总是有效的。除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果。
**注意:**未在等式列表中出现的变量是未定义的,因此无法确定它们的答案
思路:由于变量之间的倍数关系具有传递性,处理有传递性关系的问题,可以使用「并查集」,需要在并查集的「合并」与「查询」操作中维护这些变量之间的倍数关系
说明:要注意看题目中的「注意」和「数据范围」,例如:每个 Ai 或 Bi 是一个表示单个变量的字符串。所以用例 equation = ["ab", "cd"] ,这里的 ab 视为一个变量,不表示 a * b。如果面试中遇到这样的问题,一定要和面试官确认清楚题目的条件。还有 1 <= equations.length <= 20 和 values[i] > 0.0 可以避免一些特殊情况的讨论。
分析示例:
求 $\frac{a}{c}$ ,可以把 a = 2b,b = 3c 依次代入,得到 $\frac{a}{c} = \frac{2b}{c} = \frac{2·3c}{c} = 6.0$
求 $\frac{b}{a}$,很显然根据 a = 2b,知道 $\frac{b}{a} = 0.5$,也可以把 b 和 a 都转换成为 c 的倍数, $\frac{b}{a} = \frac{b}{2b} = \frac{3c}{6c} = \frac{1}{2} = 0.5$
通过上面的两个计算不难知道:可以将题目给出的 equation 中的两个变量所在的集合进行「合并」,同在一个集合中的两个变量就可以通过某种方式计算出它们的比值。具体来说,可以把不同的变量的比值转换成为相同的变量的比值,这样在做除法的时候就可以消去相同的变量,然后再计算转换成相同变量以后的系数的比值,就是题目要求的结果。统一了比较的标准,可以以 O(1) 的时间复杂度完成计算。
如果两个变量不在同一个集合中, 返回 −1.0。并且根据题目的意思,如果两个变量中 至少有一个 变量没有出现在所有 equations 出现的字符集合中,也返回 −1.0
构建有向图
通过示例的分析可以知道,题目给出的 equations 和 values 可以表示成一个图,equations 中出现的变量就是图的顶点,「分子」于「分母」的比值可以表示成一个有向关系(因为「分子」和「分母」是有序的,不可以对换),并且这个图是一个带权图,values 就是对应的有向边的权值。示例 中给出的 equations 和 values 表示的「图形表示」、「数学表示」和「代码表示」如下表所示。其中 parent[a] = b 表示:结点 a 的(直接)父亲结点是 b,与之对应的有向边的权重,记为 weight[a] = 2.0,即 weight[a] 表示结点 a 到它的 直接父亲结点 的有向边的权重
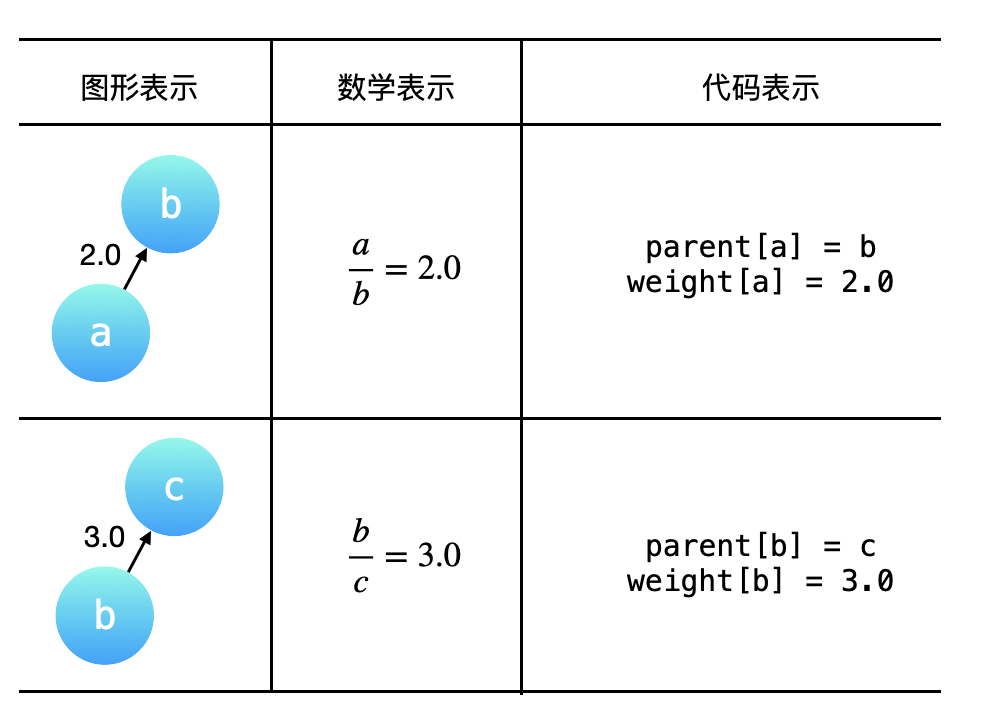
「统一变量」与「路径压缩」的关系
刚刚在分析例 1 的过程中,提到了:可以把一个一个 query 中的不同变量转换成 同一个变量,这样在计算 query 的时候就可以以 O(1) 的时间复杂度计算出结果,在「并查集」的一个优化技巧中,「路径压缩」就恰好符合了这样的应用场景。
为了避免并查集所表示的树形结构高度过高,影响查询性能。「路径压缩」就是针对树的高度的优化。「路径压缩」的效果是:在查询一个结点 a 的根结点同时,把结点 a 到根结点的沿途所有结点的父亲结点都指向根结点。如下图所示,除了根结点以外,所有的结点的父亲结点都指向了根结点。特别地,也可以认为根结点的父亲结点就是根结点自己。如下图所示:路径压缩前后,并查集所表示的两棵树形结构等价,路径压缩以后的树的高度为 2,查询性能最好。
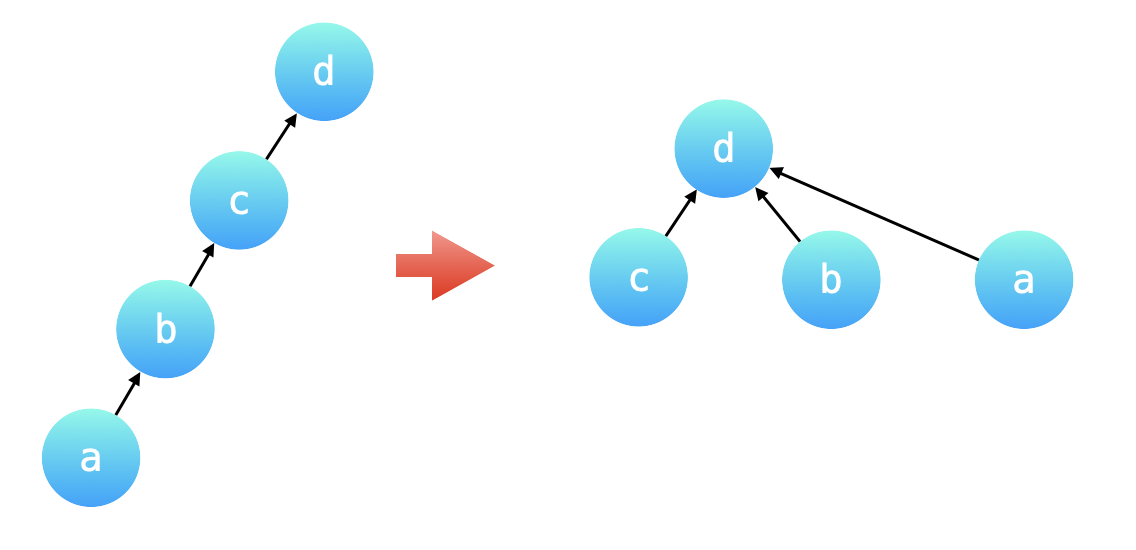
由于有「路径压缩」的优化,两个同在一个连通分量中的不同的变量,它们分别到根结点(父亲结点)的权值的比值,就是题目的要求的结果
如何在「查询」操作的「路径压缩」优化中维护权值变化
如下图所示,在结点 a 执行一次「查询」操作。路径压缩会先一层一层向上先找到根结点 d,然后依次把 c、b 、a 的父亲结点指向根结点 d
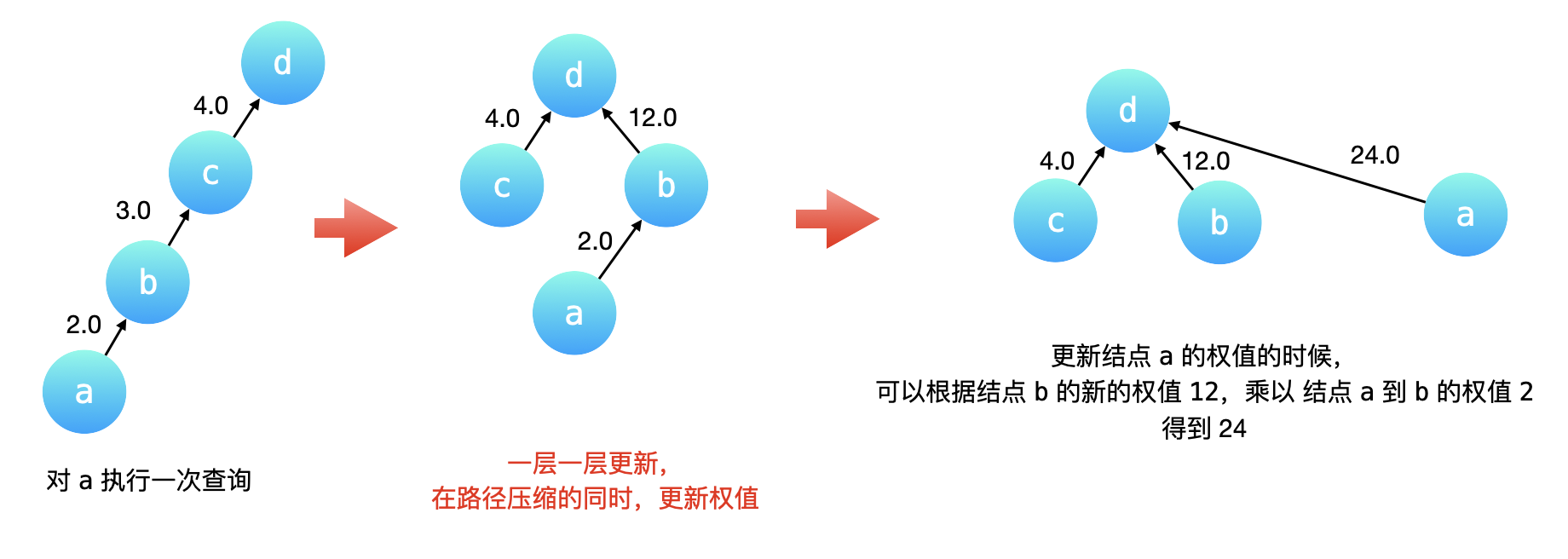
- c 的父亲结点已经是根结点了,它的权值不用更改;
- b 的父亲结点要修改成根结点,它的权值就是从当前结点到根结点经过的所有有向边的权值的乘积,因此是 3.0 乘以 4.0 也就是 12.0;
- a 的父亲结点要修改成根结点,它的权值就是依然是从当前结点到根结点经过的所有有向边的权值的乘积,但是 没有必要把这三条有向边的权值乘起来,这是因为 b 到 c,c 到 d 这两条有向边的权值的乘积在把 b 指向 d 的时候已经计算出来了。因此,a 到根结点的权值就等于 b 到根结点 d 的新的权值乘以 a 到 b 的原来的有向边的权值。
如何在「合并」操作中维护权值的变化
「合并」操作基于这样一个 很重要的前提:要合并的两棵树的高度最多为 2,换句话说两棵树都必需是「路径压缩」以后的效果,两棵树的叶子结点到根结点最多只需要经过一条有向边。
例如已知 $\frac{a}{b} = 3.0$,又已知 $\frac{d}{c} = 4.0$,现在合并结点 a 和 d 所在的集合,其实就是把 a 的根结点 b 指向 d 的根结 c,那么如何计算 b 指向 c 的这条有向边的权重呢?根据 a 经过 b 可以到达 c,a 经过 d 也可以到达 c,因此 两条路径上的有向边的权值的乘积是一定相等的。设 b 到 c 的权值为 x,那么 3.0 ⋅ x = 6.0 ⋅ 4.0 ,得 x = 8.0
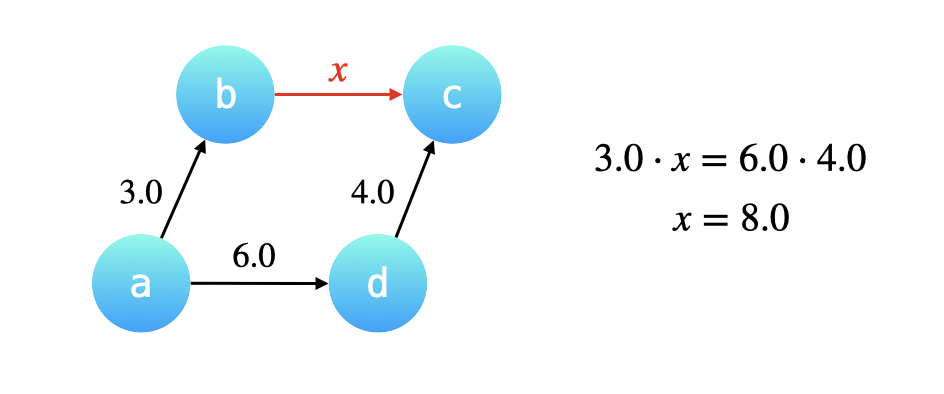
weight[rootA] = weight[b] * v / weight[a]:由于当前点的父节点直接指向了终点的父节点,所以要用路径压缩前终点的权值*当前点为起点的权值/当前点的权值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
|
var father []int
var weight []float64
func calcEquation(equations [][]string, values []float64, queries [][]string) []float64 {
// 1. 预处理
// 声明并查集
father = make([]int, 2*len(equations))
weight = make([]float64, 2*len(equations))
// 初始化并查集
initial(2 * len(equations))
// 记录所有变量 将变量的值与 id 进行映射
mp := make(map[string]int)
// 变量号
id := 0
// 遍历给定方程
for i, v := range equations {
// 将变量标号后记入字典
if _, ok := mp[v[0]]; !ok {
mp[v[0]] = id
id++
}
if _, ok := mp[v[1]]; !ok {
mp[v[1]] = id
id++
}
// 将该方程计入并查集
join(mp[v[0]], mp[v[1]], values[i])
}
// 2. 做查询
res := make([]float64, len(queries))
// 遍历所求方程
for i, v := range queries {
id1, ok1 := mp[v[0]]
id2, ok2 := mp[v[1]]
// 判该方程中变量是否未知
if !ok1 || !ok2 {
res[i] = float64(-1)
} else {
res[i] = isSame(id1, id2)
}
}
return res
}
// 初始化并查集
func initial(n int) {
for i := 0; i < n; i++ {
father[i] = i
weight[i] = float64(1)
}
}
// 并查集里寻根
func find(u int) int {
if father[u] == u {
return u
}
// 保存当前节点的父节点
origin := father[u]
// 路径压缩 更新当前节点的父节点
father[u] = find(father[u])
// 路径压缩 更新权值
weight[u] *= weight[origin]
return father[u]
}
// 判是否同根
func isSame(a, b int) float64 {
rootA := find(a)
rootB := find(b)
if rootA == rootB {
// 同一并查集中返回分别到根结点比值
return weight[a] / weight[b]
}
// 不在同一并查集中返回-1
return float64(-1)
}
// 将a->b加入并查集
func join(a, b int, val float64) {
rootA := find(a)
rootB := find(b)
if rootA == rootB {
return
}
father[rootA] = rootB
weight[rootA] = weight[b] * val / weight[a]
}
|
课程表 II
210. 课程表 II - 力扣(LeetCode)
在上上题207. 课程表基础上,要求返回学习顺序。可能会有多个正确的顺序,只要返回 任意一种 就可以。如果不可能完成所有课程,返回 一个空数组
思路:从队列取出节点时加入结果集;最后判断是否有入度非0的节点,若有则返回空数组,否则返回结果集
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
func findOrder(numCourses int, prerequisites [][]int) []int {
// 统计入度和依赖关系
indegree := make([]int, numCourses)
mp := make(map[int][]int)
for _, pairs := range prerequisites {
indegree[pairs[0]]++
mp[pairs[1]] = append(mp[pairs[1]], pairs[0])
}
// 入度为0的节点入队(起始点)
queue := []int{}
for i, v := range indegree {
if v == 0 {
queue = append(queue, i)
}
}
// 遍历图
res := make([]int, 0)
for len(queue) != 0 {
cur := queue[0]
queue = queue[1:]
res = append(res, cur)
// 判当前节点是否有后续课程
if courses, ok := mp[cur]; ok {
for _, v := range courses {
indegree[v]--
if indegree[v] == 0 {
queue = append(queue, v)
}
}
}
}
// 判是否还剩有节点入度不为0
for _, v := range indegree {
if v != 0 {
return []int{}
}
}
return res
}
|
蛇梯棋
909. 蛇梯棋 - 力扣(LeetCode)
给定一个大小为 n x n 的整数矩阵,编号遵循 转行交替方式 ,从左下角开始 (即 board[n - 1][0] ),每一行改变方向。一开始位于棋盘的左下角方格 1。每一回合,玩家需要从当前方格 curr 开始出发,前进范围[1,6](模拟骰子)。当玩家到达编号 n^2 的右上角方格时,游戏结束。
- 若
board[r][c] != -1 ,则存在 “蛇” 或 “梯子”。蛇或梯子的目的地是 board[r][c]。编号为 1 和 n^2 的方格不是任何蛇或梯子的起点
- 玩家在每次掷骰的前进过程中最多只能爬过蛇或梯子一次:就算目的地是另一条蛇或梯子的起点,玩家也不能继续移动。
返回达到编号为 n^2 的右上角方格所需的最少掷骰次数,如果不可能,则返回 -1
思路:
- 扁平化:将二维棋盘转换为一维数组
- BFS:用队列遍历,队列中存节点;字典存起点到该点的步数,同时代表是否访问过
- 队列为空,说明到不了终点;遍历队列时遇到终点直接返回步数即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
func snakesAndLadders(board [][]int) int {
// 扁平化降维
n := len(board)
nums := []int{0}
idx := 1
for i := n - 1; i >= 0; i-- {
temp := make([]int, n)
copy(temp, board[i])
if idx%2 == 0 {
slices.Reverse(temp)
}
idx++
nums = append(nums, temp...)
}
// BFS
queue := []int{1}
mp := map[int]int{}
mp[1] = 0
for len(queue) != 0 {
cur := queue[0]
queue = queue[1:]
// 判是否已到终点
if cur == n*n {
return mp[cur]
}
// 尝试从当前点掷骰子,移动 1 至 6 步
for i := 1; i <= 6; i++ {
newPos := cur + i
// 判是否越界
if newPos > n*n {
continue
}
// 判是否有蛇或梯
if nums[newPos] != -1 {
newPos = nums[newPos]
}
// 判是否已访问过
if _, ok := mp[newPos]; ok {
continue
}
queue = append(queue, newPos)
mp[newPos] = mp[cur] + 1
}
}
return -1
}
|
最小基因变化
433. 最小基因变化 - 力扣(LeetCode)
给定两个字符串和一个字符串数组,要让第一个字符串变为第二个字符串,每次只能变一个字符,而且变化后的字符串必须是数组中的,返回最少变化次数
思路:
- BFS:用队列遍历,队列中存节点;字典存起点到该点的步数,同时代表是否访问过
- 队列为空,说明到不了终点;遍历队列时遇到终点直接返回步数即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
func minMutation(startGene string, endGene string, bank []string) int {
// BFS遍历
queue := []string{startGene}
mp := map[string]int{}
mp[startGene] = 0
for len(queue) != 0 {
cur := queue[0]
queue = queue[1:]
// 判当前基因是否为最终基因
if cur == endGene {
return mp[cur]
}
// 遍历基因库
for _, str := range bank {
// 判库中基因是否已访问过或当前基因是否与库中基因一致
if _, ok := mp[str]; ok || cur == str {
continue
}
// 判当前基因是否变一个字符就与库中基因一致
if isValid(cur, str) {
mp[str] = mp[cur] + 1
queue = append(queue, str)
}
}
}
return -1
}
func isValid(str1, str2 string) bool {
cnt := 0
for i := range str1 {
if str1[i] != str2[i] {
cnt++
}
}
return cnt == 1
}
|
添加与搜索单词 - 数据结构设计
211. 添加与搜索单词 - 数据结构设计 - 力扣(LeetCode)
本题是前缀树的变种,在查询字符串是,.可以表示任何一个小写字符
思路:在匹配的过程中,如果遇到了 '.' ,则需要对当前节点的所有子树都进行DFS遍历,只要有任何一个子树能最终匹配完成,那么就代表能匹配完成。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
type WordDictionary struct {
isEnd bool
children [26]*WordDictionary
}
func Constructor() WordDictionary {
return WordDictionary{}
}
func (this *WordDictionary) AddWord(word string) {
cur := this
for _, ch := range word {
if cur.children[ch-'a'] == nil {
cur.children[ch-'a'] = new(WordDictionary)
}
cur = cur.children[ch-'a']
}
cur.isEnd = true
}
func (this *WordDictionary) Search(word string) bool {
return dfs(word, this, 0)
}
func dfs(word string, cur *WordDictionary, idx int) bool {
// 判是否到最后一个字符
if idx == len(word) {
return cur.isEnd
}
// 判当前字符是否为.
if word[idx] == '.' {
// 遍历当前节点的所有孩子
for i := 0; i < 26; i++ {
if cur.children[i] != nil && dfs(word, cur.children[i], idx+1) {
return true
}
}
return false
} else {
if cur.children[word[idx]-'a'] != nil {
return dfs(word, cur.children[word[idx]-'a'], idx+1)
}
return false
}
}
|
单词搜索 II
212. 单词搜索 II - 力扣(LeetCode)
给定一个 m x n 二维字符网格 board 和一个单词(字符串)列表 words, 返回所有二维网格上的单词 。单词必须按照字母顺序,通过 相邻的单元格 内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。
思路一:前缀树+DFS+回溯
预先将 words 中的所有字符串添加到前缀树中,而后可以用 O(∣S∣) 的时间复杂度查询当前路径是否为 words 中任一个单词的前缀
- 遍历二维网格中的所有单元格,对每个单元格 DFS
- DFS 中标记遍历过的单元格,回溯法 DFS 前标记,DFS 后恢复
- 若当前路径是 words 中的单词,则将其添加到结果集中
- 若当前路径是 words 中任一个单词的前缀,则继续搜索
- 若当前路径不是 words 中任一个单词的前缀,则返回
注意:
- TrieNode 中的
isEnd 标记属性直接换成记录以当前字符结尾的字符串 s,这样在 DFS 过程中无需记录路径
- 因为同一个单词可能在多个不同的路径中出现,所以需要使用哈希对结果集去重
- 在回溯的过程中,不需要每一步都判断完整的当前路径是否是 words 中任意一个单词的前缀;而是可以记录下路径中每个单元格所对应的前缀树结点,每次只需要判断新增单元格的字母是否是上一个单元格对应前缀树结点的子结点即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
type TrieNode struct {
word string
children [26]*TrieNode
}
func (t *TrieNode) Insert(word string) {
cur := t
for _, ch := range word {
if cur.children[ch-'a'] == nil {
cur.children[ch-'a'] = new(TrieNode)
}
cur = cur.children[ch-'a']
}
cur.word = word
}
var dirs = [4][2]int{{1, 0}, {0, 1}, {-1, 0}, {0, -1}}
func findWords(board [][]byte, words []string) []string {
// 初始化前缀树
root := new(TrieNode)
for _, word := range words {
root.Insert(word)
}
// DFS
mp := map[string]struct{}{}
var dfs func(*TrieNode, int, int)
dfs = func(cur *TrieNode, i, j int) {
// 判是否非前缀
if cur.children[board[i][j]-'a'] == nil {
return
}
cur = cur.children[board[i][j]-'a']
// 判是否找到一个有效单词
if cur.word != "" {
mp[cur.word] = struct{}{}
}
// 回溯
temp := board[i][j]
board[i][j] = '#'
for _, offset := range dirs {
x := i + offset[0]
y := j + offset[1]
if x >= 0 && y >= 0 && x < len(board) && y < len(board[0]) && board[x][y] != '#' {
dfs(cur, x, y)
}
}
board[i][j] = temp
}
// 遍历二维网格
for i := range board {
for j := range board[i] {
dfs(root, i, j)
}
}
// map去重后的结果加入结果集
res := make([]string, 0, len(mp))
for k := range mp {
res = append(res, k)
}
return res
}
|
思路二:前缀树+DFS+回溯+删除匹配过的单词(推荐)
考虑以下情况。假设给定一个所有单元格都是 a 的二维字符网格和单词列表 [“a”, “aa”, “aaa”, “aaaa”] 。当使用方法一来找出所有同时在二维网格和单词列表中出现的单词时,需要遍历每一个单元格的所有路径,会找到大量重复的单词。
为了缓解这种情况,可以将匹配到的单词从前缀树中移除,来避免重复寻找相同的单词。因为这种方法可以保证每个单词只能被匹配一次;所以也不需要再对结果集去重了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
type TrieNode struct {
word string
children [26]*TrieNode
}
func (t *TrieNode) Insert(word string) {
cur := t
for _, ch := range word {
if cur.children[ch-'a'] == nil {
cur.children[ch-'a'] = new(TrieNode)
}
cur = cur.children[ch-'a']
}
cur.word = word
}
var dirs = [4][2]int{{1, 0}, {0, 1}, {-1, 0}, {0, -1}}
func findWords(board [][]byte, words []string) []string {
// 初始化前缀树
root := new(TrieNode)
for _, word := range words {
root.Insert(word)
}
// DFS
res := []string{}
var dfs func(*TrieNode, int, int)
dfs = func(cur *TrieNode, i, j int) {
// 判是否非前缀
if cur.children[board[i][j]-'a'] == nil {
return
}
cur = cur.children[board[i][j]-'a']
// 判是否找到一个有效单词
if cur.word != "" {
res = append(res, cur.word)
// 删除匹配过的单词
cur.word = ""
}
// 回溯
temp := board[i][j]
board[i][j] = '#'
for _, offset := range dirs {
x := i + offset[0]
y := j + offset[1]
if x >= 0 && y >= 0 && x < len(board) && y < len(board[0]) && board[x][y] != '#' {
dfs(cur, x, y)
}
}
board[i][j] = temp
}
// 遍历二维网格
for i := range board {
for j := range board[i] {
dfs(root, i, j)
}
}
return res
}
|
建立四叉树
427. 建立四叉树 - 力扣(LeetCode)
给定一个 n * n 矩阵 grid ,矩阵由若干 0 和 1 组成。用四叉树表示该矩阵 grid 。四叉树每个节点有四个子节点还有有两个属性:
思路:DFS递归分治
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
func construct(grid [][]int) *Node {
var dfs func(int, int, int, int) *Node
dfs = func(startX, startY, endX, endY int) *Node {
// 检查当前n*n网格中值是否相同
n := endX - startX
for i := startX; i < endX; i++ {
for j := startY; j < endY; j++ {
if grid[i][j] != grid[startX][startY] {
// 非叶子节点
return &Node{
TopLeft: dfs(startX, startY, endX-n/2, endY-n/2),
TopRight: dfs(startX, startY+n/2, endX-n/2, endY),
BottomLeft: dfs(startX+n/2, startY, endX, endY-n/2),
BottomRight: dfs(startX+n/2, startY+n/2, endX, endY),
}
}
}
}
// 是叶节点
return &Node{Val: grid[startX][startY] == 1, IsLeaf: true}
}
return dfs(0, 0, len(grid), len(grid))
}
|
- 时间复杂度:O(n^2 logn)
- 空间复杂度:O(logn)
省份数量
547. 省份数量 - 力扣(LeetCode)
给定一个n*n矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。返回矩阵中 省份 的数量。省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
思路:并查集
将相连城市加入并查集,直接相连和间接相连的城市都在同一集合中。由于路径压缩,同一集合指向同一父亲,最后统计父亲个数即是省份个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
var father []int
func findCircleNum(isConnected [][]int) int {
// 初始化并加入并查集
father = make([]int, len(isConnected))
initial(len(isConnected))
for i := range isConnected {
for j := range isConnected[i] {
if isConnected[i][j] == 1 {
join(i, j)
}
}
}
// 路径压缩
for i := 0; i < len(isConnected); i++ {
find(i)
}
// 统计集合个数(不同father的个数)
mp := map[int]bool{}
for _, v := range father {
mp[v] = true
}
return len(mp)
}
func initial(n int) {
for i := 0; i < n; i++ {
father[i] = i
}
}
func find(a int) int {
if father[a] == a {
return a
}
father[a] = find(father[a])
return father[a]
}
func isSame(a, b int) bool {
a = find(a)
b = find(b)
return a == b
}
func join(a int, b int) {
a = find(a)
b = find(b)
if a == b {
return
}
father[a] = b
}
|
重新规划路线
1466. 重新规划路线 - 力扣(LeetCode)
路线用 connections 表示,其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。重新规划路线方向,使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。
思路:dfs
使用 1 标记原方向的边,使用 0 标记反向边。然后从 0 号点开始遍历,访问到某个新的点时,所经过的边被 1 标记,就令答案加 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
func minReorder(n int, connections [][]int) int {
// 第一维是起点 第二维是终点 第三维标记位 1-原边 0-反向边
edges := make([][][]int, n)
// 标记原边和反向边
for _, connection := range connections {
edges[connection[0]] = append(edges[connection[0]], []int{connection[1], 1})
edges[connection[1]] = append(edges[connection[1]], []int{connection[0], 0})
}
// dfs 从0出发统计原边个数
res := 0
var dfs func(int, int)
dfs = func(cur int, father int) {
// 遍历从当前点出发的所有终点
for _, v := range edges[cur] {
// 判终点是否已遍历过
if v[0] == father {
continue
}
// 若为原边则结果加一
res += v[1]
// 向深遍历 终点作为出发点 出发点为父
dfs(v[0], cur)
}
}
dfs(0, -1)
return res
}
|
迷宫中离入口最近的出口
1926. 迷宫中离入口最近的出口 - 力扣(LeetCode)
给一个 m x n 的迷宫矩阵 maze (下标从 0 开始),矩阵中有空格子(用 '.' 表示)和墙(用 '+' 表示)。用 entrance = [entrancerow, entrancecol] 表示一开始所在格子的行和列。每一步操作,可以往 上,下,左 或者 右 移动一个格子。不能进入墙所在的格子,目标是找到离 entrance 最近 的出口。出口 的含义是 maze 边界 上的 空格子。entrance 格子 不算 出口。返回从 entrance 到最近出口的最短路径的 步数 ,如果不存在这样的路径,返回 -1
思路:BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
func nearestExit(maze [][]byte, entrance []int) int {
// BFS
dis := [4][2]int{{1, 0}, {-1, 0}, {0, 1}, {0, -1}}
queue := [][]int{{entrance[0], entrance[1], 0}}
maze[entrance[0]][entrance[1]] = '+'
for len(queue) != 0 {
curX := queue[0][0]
curY := queue[0][1]
curLength := queue[0][2]
queue = queue[1:]
for _, offset := range dis {
nextX := curX + offset[0]
nextY := curY + offset[1]
if nextX >= 0 && nextY >= 0 && nextX < len(maze) && nextY < len(maze[0]) && maze[nextX][nextY] == '.' {
if nextX == 0 || nextX == len(maze)-1 || nextY == 0 || nextY == len(maze[0])-1 {
return curLength + 1
}
maze[nextX][nextY] = '+'
queue = append(queue, []int{nextX, nextY, curLength + 1})
}
}
}
return -1
}
|
判断二分图
785. 判断二分图 - 力扣(LeetCode)
给定一个图,判断是否为二分图。二分图定义:如果能将一个图的节点集合分割成两个独立的子集 A 和 B ,并使图中的每一条边的两个节点一个来自 A 集合,一个来自 B 集合
- 这个图可能不是连通图,也就是说两个节点
u 和 v 之间可能不存在一条连通彼此的路径。
思路:BFS从每个未遍历过的顶点开始遍历整个连通域,遍历的过程中用两种不同的颜色对顶点进行染色,相邻顶点染成相反的颜色。
BFS过程中若发现相邻的顶点被染成了相同的颜色,说明它不是二分图;反之,如果所有点都染色成功,说明它是二分图。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
func isBipartite(graph [][]int) bool {
// -1和1表示两种不同颜色,0表示未被访问
visited := make([]int, len(graph))
// 因为图中可能含有多个连通域,所以需要判断是否存在顶点未被访问,若存在则从它开始再进行一轮 bfs 染色
for i := range graph {
// 判该点是否被访问过
if visited[i] != 0 {
continue
}
// 从该点开始BFS
// 该点入队
queue := []int{i}
// 标记该点颜色
visited[i] = 1
for len(queue) != 0 {
cur := queue[0]
queue = queue[1:]
// 遍历当前点的所有邻接点
for _, v := range graph[cur] {
// 判两点颜色是否相同
if visited[cur] == visited[v] {
// 若当前点的某个邻接点已经被染过色了,且颜色和当前点相同,说明此无向图无法被正确染色,返回 false
return false
}
// 判该邻接点是否未被访问过
if visited[v] == 0 {
// 置该邻接点颜色与当前点颜色相反
visited[v] = -visited[cur]
// 该邻接点入队
queue = append(queue, v)
}
}
}
}
return true
}
|
- 时间复杂度是 O(N+M)
- 空间复杂度是 O(N)
K 站中转内最便宜的航班
787. K 站中转内最便宜的航班 - 力扣(LeetCode)
同上 bellman_ford 单源有限最短路
水壶问题
有两个水壶,容量分别为 x 和 y 升。水的供应是无限的。确定是否有可能使用这两个壶准确得到 target 升。可以:
- 装满任意一个水壶
- 清空任意一个水壶
- 将水从一个水壶倒入另一个水壶,直到接水壶已满,或倒水壶已空。
思路:DFS+栈
在任意一个时刻,此问题的状态可以由两个数字决定:X 壶中的水量,以及 Y 壶中的水量。在任意一个时刻,可以且仅可以采取以下几种操作:
-
把 X 壶的水灌进 Y 壶,直至灌满或倒空
-
把 Y 壶的水灌进 X 壶,直至灌满或倒空
-
把 X 壶灌满
-
把 Y 壶灌满
-
把 X 壶倒空
-
把 Y 壶倒空
因此,本题可以使用 DFS 来解决。搜索中的每一步以 remain_x, remain_y 作为状态,即表示 X 壶和 Y 壶中的水量。在每一步搜索时,依次尝试所有的操作,递归地搜索下去。这可能会导致陷入无止境的递归,因此还需要使用一个哈希表存储所有已经搜索过的 remain_x, remain_y 状态,保证每个状态至多只被搜索一次。
在实际的代码编写中,由于 DFS 导致的递归层数很大,因此可以使用栈来模拟递归,避免了真正使用递归而导致的问题
注意:由于哈希表key不能为数组,所以可以将remain_x*10000+remain_y当作key存入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
func canMeasureWater(x int, y int, target int) bool {
stack := [][]int{{0, 0}}
mp := map[int]bool{}
// []int -> int
hash := func(state []int) int {
return state[0]*10000 + state[1]
}
for len(stack) != 0 {
// 判该状态是否被遍历过
if mp[hash(stack[len(stack)-1])] {
stack = stack[:len(stack)-1]
continue
}
// 标记当前状态
mp[hash(stack[len(stack)-1])] = true
// 取出当前状态
remain_x, remain_y := stack[len(stack)-1][0], stack[len(stack)-1][1]
stack = stack[:len(stack)-1]
// 判当前状态是否满足目标
if remain_x == target || remain_y == target || remain_x+remain_y == target {
return true
}
// 遍历所有状态并入栈
// 1.灌满x
stack = append(stack, []int{x, remain_y})
// 2.灌满y
stack = append(stack, []int{remain_x, y})
// 3.倒空x
stack = append(stack, []int{0, remain_y})
// 4.倒空y
stack = append(stack, []int{remain_x, 0})
// 5.x倒入y
stack = append(stack, []int{max(0, remain_x-(y-remain_y)), min(remain_y+remain_x, y)})
// 6.y倒入x
stack = append(stack, []int{min(remain_x+remain_y, x), max(0, remain_y-(x-remain_x))})
}
return false
}
|
- 时间复杂度:O(xy),状态数最多有 (x+1)(y+1) 种,对每一种状态进行深度优先搜索的时间复杂度为 O(1),因此总时间复杂度为 O(xy)。
- 空间复杂度:O(xy),由于状态数最多有 (x+1)(y+1) 种,哈希集合中最多会有 (x+1)(y+1) 项,因此空间复杂度为 O(xy)
扫雷游戏
529. 扫雷游戏 - 力扣(LeetCode)
给一个大小为 m x n 二维字符矩阵 board ,表示扫雷游戏的盘面,其中:
'M' 代表一个 未挖出的 地雷,'E' 代表一个 未挖出的 空方块,'B' 代表没有相邻(上,下,左,右,和所有4个对角线)地雷的 已挖出的 空白方块,- 数字(
'1' 到 '8')表示有多少地雷与这块 已挖出的 方块相邻,
'X' 则表示一个 已挖出的 地雷。
给一个整数数组 click ,其中 click = [clickr, clickc] 表示在所有 未挖出的 方块('M' 或者 'E')中的下一个点击位置(clickr 是行下标,clickc 是列下标)。
根据以下规则,返回相应位置被点击后对应的盘面:
- 如果一个地雷(
'M')被挖出,游戏就结束了- 把它改为 'X' 。
- 如果一个 没有相邻地雷 的空方块(
'E')被挖出,修改它为('B'),并且所有和其相邻的 未挖出 方块都应该被递归地揭露。
- 如果一个 至少与一个地雷相邻 的空方块(
'E')被挖出,修改它为数字('1' 到 '8' ),表示相邻地雷的数量。
- 如果在此次点击中,若无更多方块可被揭露,则返回盘面。
思路:DFS
题目要求根据规则来展示执行一次点击操作后游戏面板的变化,所以只要明确该扫雷游戏的规则,并用代码模拟出来即可。着眼于题目的规则,会发现总共分两种情况:
- 当前点击的是「未挖出的地雷」,将其值改为 X 即可。
- 当前点击的是「未挖出的空方块」,统计它周围相邻的方块里地雷的数量
cnt(即 M 的数量)。如果 cnt 为零,即执行规则 2,此时需要将其改为 B,且递归地处理周围的八个未挖出的方块,递归终止条件即为规则 4,没有更多方块可被揭露的时候。否则执行规则 3,将其修改为数字即可。
整体看来,一次点击过程会从一个位置出发,逐渐向外圈扩散,所以利用「搜索」的方式来实现。这里以DFS为例:定义递归函数 dfs(x, y) 表示当前在 (x,y) 点,执行扫雷规则的情况,只要按照上面理出来的情况来进行模拟即可,在 cnt 为零的时候,对当前点相邻的未挖出的方块调用递归函数,否则将其改为数字,结束递归。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
var dis = [8][2]int{{1, 0}, {-1, 0}, {0, 1}, {0, -1}, {-1, -1}, {-1, 1}, {1, 1}, {1, -1}}
func updateBoard(board [][]byte, click []int) [][]byte {
// 判是否点击到雷
if board[click[0]][click[1]] == 'M' {
board[click[0]][click[1]] = 'X'
} else {
dfs(board, click[0], click[1])
}
return board
}
func dfs(board [][]byte, i, j int) {
// 统计当前位置相邻八个位置的雷数
cnt := 0
for _, offset := range dis {
x := i + offset[0]
y := j + offset[1]
if x >= 0 && y >= 0 && x < len(board) && y < len(board[0]) && board[x][y] == 'M' {
cnt++
}
}
// 判当前位置相邻八个位置是否无雷
if cnt == 0 {
board[i][j] = 'B'
// 向相邻未点击的格DFS
for _, offset := range dis {
x := i + offset[0]
y := j + offset[1]
if x >= 0 && y >= 0 && x < len(board) && y < len(board[0]) && board[x][y] == 'E' {
dfs(board, x, y)
}
}
} else {
board[i][j] = byte(cnt+'0')
}
}
|
- 时间复杂度:O(nm),其中 n 和 m 分别代表面板的宽和高。最坏情况下会遍历整个面板
- 空间复杂度:O(nm),空间复杂度取决于递归的栈深度,而递归栈深度在最坏情况下有可能遍历整个面板而达到 O(nm)
矩阵中的最长递增路径
329. 矩阵中的最长递增路径 - 力扣(LeetCode)
给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。对于每个单元格,可以往上,下,左,右四个方向移动。不能在 对角线 方向上移动或移动到边界外
思路:DFS
DFS从每个单元格出发的最长递增路径,同时存储该路径长度,当遇到计算过的单元格直接使用即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
func longestIncreasingPath(matrix [][]int) int {
// 记忆化存储各个单元格出发的最长递增路径长度
memo := make([][]int, len(matrix))
for i := range memo {
memo[i] = make([]int, len(matrix[i]))
}
// dfs
dis := [4][2]int{{1, 0}, {-1, 0}, {0, 1}, {0, -1}}
var dfs func(int, int) int
dfs = func(i, j int) int {
// 判matrix[i][j]是否遍历过
if memo[i][j] != 0 {
return memo[i][j]
}
// 标记自身为起点初始路径长度为1
memo[i][j] = 1
for _, offset := range dis {
x := i + offset[0]
y := j + offset[1]
if x >= 0 && y >= 0 && x < len(matrix) && y < len(matrix[0]) && matrix[x][y] > matrix[i][j] {
// max(之前不同的前进方向得到的, 当前前进方向)
memo[i][j] = max(memo[i][j], dfs(x, y)+1)
}
}
return memo[i][j]
}
// 遍历单元格起点
res := 0
for i := range matrix {
for j := range matrix[i] {
res = max(res, dfs(i, j))
}
}
return res
}
|
LCR 130. 衣橱整理
LCR 130. 衣橱整理 - 力扣(LeetCode)
给定m x n 的二维矩阵 grid,其中 grid[i][j] 代表一个需要整理的格子。整理师自 grid[0][0] 开始 逐行逐列 地整理每个格子。整理规则为:在整理过程中,可以选择 向右移动一格 或 向下移动一格,但不能移动到衣柜之外。同时,不需要整理 digit(i) + digit(j) > cnt 的格子,其中 digit(x) 表示数字 x 的各数位之和。返回整理师 总共需要整理多少个格子
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
func wardrobeFinishing(m int, n int, cnt int) int {
visited := make([][]bool, m)
for i := range visited {
visited[i] = make([]bool, n)
}
var dfs func(i, j int) int
dfs = func(i, j int) int {
if i >= m || j >= n || visited[i][j] || i%10+i/10+j%10+j/10 > cnt {
return 0
}
visited[i][j] = true
return 1 + dfs(i+1, j) + dfs(i, j+1)
}
return dfs(0, 0)
}
|
克隆图
133. 克隆图 - 力扣(LeetCode)
给定无向连通图中一个节点的引用,返回该图的深拷贝(克隆)
思路一:非递归,用栈实现(不推荐)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
|
func cloneGraph(node *Node) *Node {
if node == nil {
return node
}
stack := make([]*Node, 0)
newStack := make([]*Node, 0)
mp := make(map[int]*Node)
temp := make(map[int]bool)
// 给定节点入栈
stack = append(stack, node)
temp[node.Val] = true
// 遍历所有旧节点创建对应新节点
for len(stack) != 0 {
// 取出一个节点作为当前节点
cur := stack[len(stack)-1]
stack = stack[:len(stack)-1]
// 将当前节点的邻居节点入栈
for _, v := range cur.Neighbors {
// 未遍历过该节点
if !temp[v.Val] {
stack = append(stack, v)
temp[v.Val] = true
}
}
// 构造当前节点的拷贝
newNode := &Node{
Val: cur.Val,
Neighbors: cur.Neighbors,
}
// 将新节点存入字典
mp[newNode.Val] = newNode
// 将新节点存入新栈
newStack = append(newStack, newNode)
}
for len(newStack) != 0 {
// 取出一个节点作为当前节点
cur := newStack[len(newStack)-1]
newStack = newStack[:len(newStack)-1]
// 保存当前节点的新邻居节点
temp := make([]*Node, 0)
// 遍历当前节点的邻居节点
for i := 0; i < len(cur.Neighbors); i++ {
// 在字典中找到对应的新节点
if v, ok := mp[cur.Neighbors[i].Val]; ok {
// 保存当前节点的新邻居节点
temp = append(temp, v)
}
}
// 修改所有邻居节点为新节点
cur.Neighbors = nil
cur.Neighbors = append(cur.Neighbors, temp...)
}
// 字典中找给定节点对应的新节点
if v, ok := mp[node.Val]; ok {
return v
}
return nil
}
|
思路二:递归DFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
func cloneGraph(node *Node) *Node {
// 记录旧->新节点的对应
mp := make(map[*Node]*Node)
return clone(node, mp)
}
func clone(cur *Node, mp map[*Node]*Node) *Node {
if cur == nil {
return cur
}
// 字典中存在该节点对应的新节点
if v, ok := mp[cur]; ok {
return v
}
// 构建新节点
newNode := &Node{
Val: cur.Val,
Neighbors: make([]*Node, len(cur.Neighbors)),
}
// 更新字典:旧节点->新节点
mp[cur] = newNode
// 遍历当前节点的邻居节点
for i := 0; i < len(cur.Neighbors); i++ {
newNode.Neighbors[i] = clone(cur.Neighbors[i], mp)
}
return newNode
}
|
01 矩阵
542. 01 矩阵 - 力扣(LeetCode)
思路一:对每个元素BFS(超时)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
|
func updateMatrix(mat [][]int) [][]int {
// 遍历给定矩阵
for i := 0; i < len(mat); i++ {
for j := 0; j < len(mat[0]); j++ {
// 遇到元素1
if mat[i][j] == 1 {
queue := make([][2]int, 0)
// 当前元素入队
queue = append(queue, [2]int{i, j})
// 记录距离
dist := 0
// 标记是否找到最近元素0
isFind := false
// 标记该坐标是否被遍历过
mp := make(map[[2]int]bool)
// BFS
for len(queue) != 0 && !isFind {
// 记录本层元素数
count := len(queue)
// 遍历本层所有元素
for k := 0; k < count && !isFind; k++ {
// 记录队首元素后出队
curI, curJ := queue[0][0], queue[0][1]
queue = queue[1:]
// 标记当前元素已遍历过
mp[[2]int{curI, curJ}] = true
// 找到元素0
if mat[curI][curJ] == 0 {
// 修改矩阵对应元素为距离
mat[i][j] = dist
// 标记找到最近元素0
isFind = true
}
// 上方元素入队
if curI != 0 && !mp[[2]int{curI - 1, curJ}] {
queue = append(queue, [2]int{curI - 1, curJ})
}
// 下方元素入队
if curI != len(mat)-1 && !mp[[2]int{curI + 1, curJ}] {
queue = append(queue, [2]int{curI + 1, curJ})
}
// 左方元素入队
if curJ != 0 && !mp[[2]int{curI, curJ - 1}] {
queue = append(queue, [2]int{curI, curJ - 1})
}
// 右方元素入队
if curJ != len(mat[0])-1 && !mp[[2]int{curI, curJ + 1}] {
queue = append(queue, [2]int{curI, curJ + 1})
}
}
// 距离+1
dist++
}
}
}
}
return mat
}
|
思路二BFS:
初始标记1,从0向四周寻找,遇到标记则修改其值,再入队继续向四周寻找
- 先遍历一遍矩阵,遇到
0入队,遇到1标记为-1
- 遍历队列,若四当前节点四周被标记,说明其非
0,则修改其值为当前值加1,再将其入队,继续向四周寻找被标记为-1的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
func updateMatrix(mat [][]int) [][]int {
queue := make([][2]int, 0)
// 遍历给定矩阵
for i := 0; i < len(mat); i++ {
for j := 0; j < len(mat[0]); j++ {
// 遇到元素0
if mat[i][j] == 0 {
// 坐标入队
queue = append(queue, [2]int{i, j})
} else {
// 标记当前元素需要更新
mat[i][j] = -1
}
}
}
// 设置四周偏移量
ds := [4][2]int{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}
// 遍历队列
for len(queue) != 0 {
// 保存队首后出队
x, y := queue[0][0], queue[0][1]
queue = queue[1:]
// 遍历当前元素的四周
for _, offset := range ds {
// 给当前元素下标设置偏移量
curX := x + offset[0]
curY := y + offset[1]
// 坐标有效且对应元素需要更新
if curX >= 0 && curY >= 0 && curX < len(mat) && curY < len(mat[0]) && mat[curX][curY] == -1 {
// 更新元素值
mat[curX][curY] = mat[x][y] + 1
// 更新后元素的下标入队
queue = append(queue, [2]int{curX, curY})
}
}
}
return mat
}
|