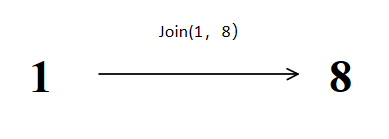理论基础
二叉树和回溯算法章节中已经讲过深搜和广搜,二叉树的遍历就是深搜和广搜在二叉树结构上的应用, 而回溯算法本身就是深搜,只不过利用其回溯的过程。在图论中,深搜和广搜就是在图上的遍历,图的存储方式一般是 邻接表和邻接矩阵。
dfs 与 bfs 区别
深度优先搜索(dfs)和广度优先搜索(bfs)区别:
- dfs是可一个方向去搜,不到黄河不回头,直到遇到绝境了,搜不下去了,再换方向(换方向的过程就涉及到了回溯)。
- bfs是先把本节点所连接的所有节点遍历一遍,走到下一个节点的时候,再把连接节点的所有节点遍历一遍,搜索方向更像是广度,四面八方的搜索过程。
dfs模板
正是因为dfs搜索可一个方向,并需要回溯,所以用递归的方式来实现是最方便的。回溯操作就在递归函数的下面,递归和回溯是相辅相成的。
1
2
3
4
5
6
7
8
9
10
11
12
|
void dfs(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本节点所连接的其他节点) {
处理节点;
dfs(图,选择的节点); // 递归
回溯,撤销处理结果
}
}
|
深搜三部曲
- 确认递归函数,参数:在写递归函数的过程中,发现需要什么参数,再去补充;一般深搜需要 二维数组数组结构保存所有路径,需要一维数组保存单一路径
- 确认终止条件:终止条件不仅是结束本层递归,同时也是收获结果的时候;很多dfs写法,没有写终止条件,其实终止条件写在了下面dfs递归的逻辑里了,也就是不符合条件,直接不会向下递归
- 处理目前搜索节点出发的路径:一般这里就是一个for循环的操作,去遍历 目前搜索节点 所能到的所有节点
广搜的使用场景
广搜的搜索方式就适合于解决两个点之间的最短路径问题
因为广搜是从起点出发,以起始点为中心一圈一圈进行搜索,一旦遇到终点,记录之前走过的节点就是一条最短路。
当然,也有一些问题是广搜 和 深搜都可以解决的,例如岛屿问题,这类问题的特征就是不涉及具体的遍历方式,只要能把相邻且相同属性的节点标记上就行。
代码框架
很多网上的资料都是直接说BFS用队列来实现,其实仅仅需要一个容器能保存遍历过的元素就可以,用队列,还是用栈,甚至用数组,都是可以的。
用队列的话,就是保证方向统一,例如统一顺时针或者逆时针,因为队列是先进先出,所以加入元素和弹出元素的顺序是没有改变的
如果用栈的话,就是第一圈是方向1,第二圈是反方向,第三圈又回到方向1。,因为栈是先进后出,加入元素和弹出元素的顺序改变了
那么广搜需要注意搜索的顺序吗? 不需要!所以用队列,还是用栈都是可以的,但大家都习惯用队列了,所以下面也用队列来给出广搜代码模板
1
2
3
4
5
6
7
8
9
10
11
|
func bfs(参数) {
// 定义队列
// 起始节点入队
for len(queue) != 0 {
// 取队首元素
for 选择:本节点所连接的其他节点 {
// 处理节点
// 新节点入队
}
}
}
|
并查集
并查集用来解决连通性问题:判断两个元素是否在同一个集合里
- 将两个元素添加到一个集合中
- 判断两个元素是否在一个集合
原理
将A,B两个元素放在同一集合(连通),只需要用一个一维数组来表示,即father[A] = B,father[B] = B,这样就表示AB连通了;根据A可以找到B,根据B可以找到B,AB最终都会找到B,即AB同根,表示两个个元素在一个集合里
同理,将A,B,C三个元素放在同一个集合(连通),即:father[A] = B,father[B] = C,father[C] = C,这样就表示ABC连通了;根据A可以找到B,根据B可以找到C,根据C可以找到C,ABC最终都会找到C,即ABC同根,表示三个元素在一个集合里,寻根过程:
1
2
3
4
|
func find(u int) int {
if u == father[u] return u // 如果根就是自己,直接返回
else return find(father[u]) // 如果根不是自己,就根据数组下标一层一层向下找根
}
|
father数组初始化的时候要 father[i] = i,默认自己指向自己
判断两个元素是否在同一个集合里,若通过find函数找到两个元素属于同一个根的话,那么这两个元素就是同一个集合,代码如下:
1
2
3
4
5
|
func isSame(a int, b int) bool {
a = find(a)
b = find(b)
return a == b
}
|
路径压缩
如果让所有节点都直接挂载根下,这样在寻根的时候就只需要一步,想要达到这样的效果,就需要 路径压缩,将非根节点的所有节点直接指向根节点。
实现:在递归的过程中,让 father[u] 接住递归函数 find(father[u]) 的返回结果
因为 find 函数向上寻找根节点时,father[u] 表述 u 的父节点,那么让 father[u] 直接获取find函数返回的根节点,这样就让节点 u 的父节点变成了根节点,即根节点直接指向了u
1
2
3
4
5
|
// 并查集里寻根的过程
func find(u int) int {
if father[u] == u return u
else return father[u] = find(father[u]) // 路径压缩
}
|
并查集模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
var father []int
func validPath(n int, edges [][]int, source int, destination int) bool {
father = make([]int, n)
initial(n)
for i := range edges {
join(edges[i][0], edges[i][1])
}
return isSame(source, destination)
}
// 并查集初始化
func initial(n int) {
for i := 0; i < n; i++ {
father[i] = i
}
}
// 并查集里寻根
func find(u int) int {
if father[u] == u {
return u
}
father[u] = find(father[u])
return father[u]
}
// 判断a和b是否找到同一个根
func isSame(a int, b int) bool {
a = find(a)
b = find(b)
return a == b
}
// 边a->b加入并差集
func join(a int, b int) {
a = find(a)
b = find(b)
if a == b {
return // 同根说明已经在一个集合里
}
father[a] = b
}
|
注意:join函数里要有find函数进行寻根的过程,这样就保证元素在有向图里是强连通的
模拟过程
1、join(1, 8)
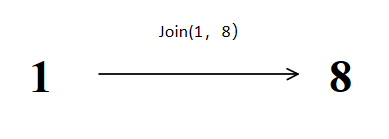
2、join(3, 8)
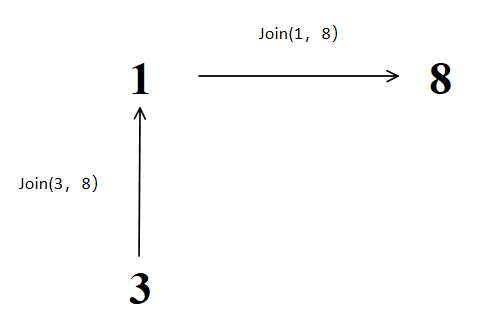
3指向1不指向8是因为在join函数里分别对3和8寻根之后,3的根为3,8的根为1,再进行关联就为3指向1
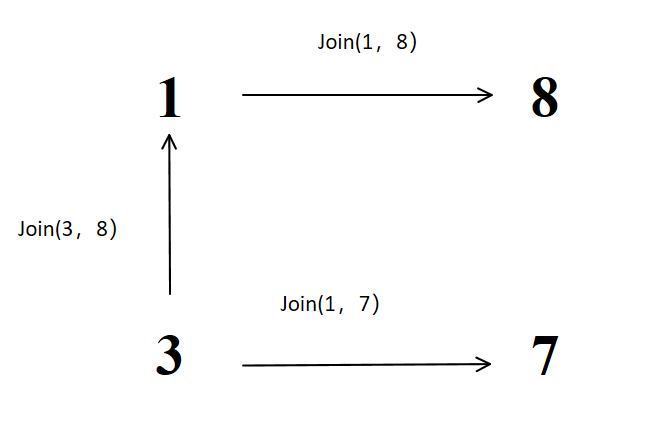
3、join(1, 7)
4、join(8, 5)
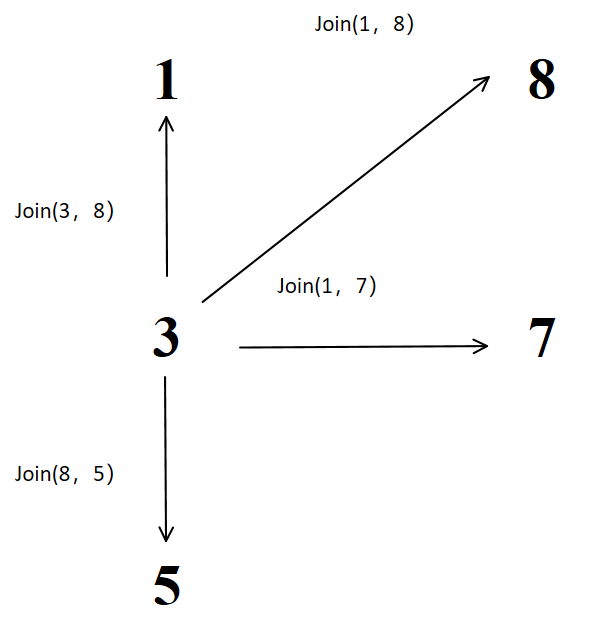
这里8的根是3,那么3应该指向5,因为是在join函数里分别对a和b进行了寻根之后再进行的关联
但是这里1不指向8了,3直接指向了8,这是因为路经压缩,这减少了下次查询的路径长度
5、join(2, 9)
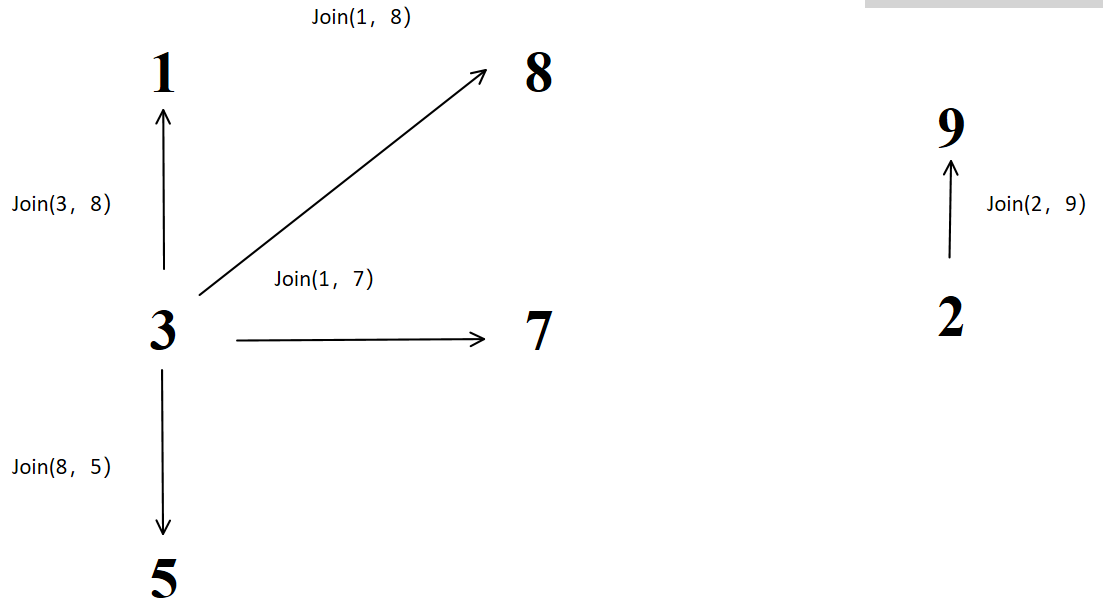
6、join(6, 9)
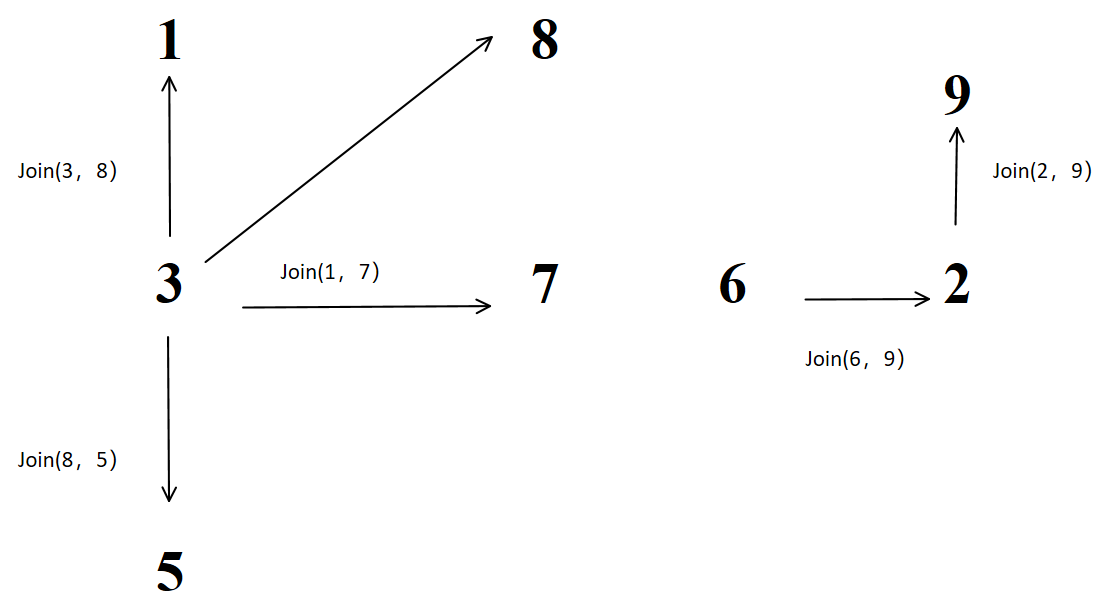
因为9的根为 2,所以用6指向2
13578是同一个集合,269是同一个集合
复杂度分析
路径压缩版并查集
- 空间复杂度: O(n) ,申请一个father数组
- 路径压缩后的并查集时间复杂度在O(logn)与O(1)之间,且随着查询或者合并操作的增加,时间复杂度会越来越趋于O(1)
在第一次查询的时候,相当于是n叉树上从叶子节点到根节点的查询过程,时间复杂度是logn,但路径压缩后,后面的查询操作都是O(1),而 join 函数和 isSame函数里涉及的查询操作也是一样的过程
所有可能的路径
797. 所有可能的路径 - 力扣(LeetCode)
给定一个二维数组含有n个元素,表示有向无环图,每个元素表示该元素下标节点能到达的节点(一条有向边),返回节点0到节点n-1的所有路径
- 确认递归函数,参数:一个图是用来遍历,一个是目前遍历的节点;单一路径和路径集合可以放在全局变量
- 确认终止条件:当目前遍历的节点为最后一个节点的时候,就找到了一条从出发点到终止点的路径
- 处理目前搜索节点出发的路径:得到当前遍历节点的指向的下一个节点,将选中的节点加入到单一路径中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
var path []int // 节点0到节点n-1的所有路径
var res [][]int // 节点0到节点n-1的一条路径
func allPathsSourceTarget(graph [][]int) [][]int {
path = make([]int, 0) // 力扣中全局变量需要重新初始化,否则会携带之前测试case的答案
res = make([][]int, 0)
path = append(path, 0) // 从节点0出发
dfs(graph, 0)
return res
}
func dfs(graph [][]int, cur int) {
// 终止条件:当前遍历节点是节点n-1
if cur == len(graph)-1 {
temp := make([]int, len(path))
copy(temp, path)
res = append(res, temp) // 将找到的一条路径加入结果集
return
}
for i := 0; i < len(graph[cur]); i++ { // 遍历当前节点连接的所有节点
path = append(path, graph[cur][i]) // 将遍历到的节点加入路径
dfs(graph, graph[cur][i]) // 进入下一层递归
path = path[:len(path)-1] // 回溯 在路径中撤销本节点
}
}
|
岛屿数量
200. 岛屿数量 - 力扣(LeetCode)
给定一个二维数组,表示一块区域;元素由0和1组成,1代表陆地,0代表海洋;若陆地被海洋包裹,则说明是岛屿;假设该区域四条边外是海洋;被海洋包裹的多块水平或垂直相连陆地看作一个岛屿;返回该区域中岛屿的数量
本题思路:遍历一遍所有节点;每遇到一个陆地节点且没有被标记过,计数器就加一,然后把该陆地节点所能遍历到的陆地都标记上;在遇到标记过的陆地节点和海洋节点的时候直接跳过;这样计数器就是最终岛屿的数量
把陆地节点所能遍历到的陆地都标记上可以使用 DFS,BFS或者并查集
对于本题来说,DFS和BFS都是对一个节点进行四周遍历,区别是DFS用递归栈来保存遍历过的状态,BFS用队列来保存遍历过的状态
DFS
- 确认递归函数,参数:一个是图用来遍历,一个是目前遍历的节点的横纵坐标(坐标用来访问四周节点和设置标记节点变量);保存节点标记的变量可以放在全局变量
- 确认终止条件:索引越界或遇到海洋
- 处理目前搜索节点出发的路径:得到当前遍历节点的指向的下一个节点
注意:本题是网格,dfs时要四个方向都搜
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
var visited [][]bool
func numIslands(grid [][]byte) int {
res := 0
visited = make([][]bool, len(grid))
for i := range visited {
visited[i] = make([]bool, len(grid[i]))
}
for i := range grid {
for j := range grid[i] {
if grid[i][j] == '1' && !visited[i][j] { // 遇到陆地节点且没有被标记过
res += 1
dfs(grid, i, j)
}
}
}
return res
}
func dfs(grid [][]byte, x int, y int) {
if grid[x][y] == '0' || visited[x][y] { // 遇到海洋节点或标记过的节点
return
}
visited[x][y] = true // 标记节点
if x != len(grid)-1 { // x没到最后一层
dfs(grid, x+1, y) // 递归 向下探索
}
if y != len(grid[x])-1 { // y没到最后一列
dfs(grid, x, y+1) // 递归 向右探索
}
if x != 0 { // x不是第一层
dfs(grid, x-1, y) // 递归 向上探索
}
if y != 0 { // y不是第一列
dfs(grid, x, y-1) // 递归 向左探索
}
}
|
DFS优化:将遍历过的陆地直接置为0
注意:在终止条件中,先判断索引,再判断是否遇到海洋,防止越界;同理由于判断列数要用到行数,所有也要放在行数判断之后
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
func numIslands(grid [][]byte) int {
res := 0
for i := range grid {
for j := range grid[i] {
if grid[i][j] == '1' { // 遇到陆地节点且没有被标记过
res += 1
dfs(grid, i, j)
}
}
}
return res
}
func dfs(grid [][]byte, x int, y int) {
// 下标越界或遇到海洋节点
if x < 0 || y < 0 || x == len(grid) || y == len(grid[x]) || grid[x][y] == '0' {
return
}
grid[x][y] = '0' // 标记节点
dfs(grid, x+1, y) // 递归 向下探索
dfs(grid, x, y+1) // 递归 向右探索
dfs(grid, x-1, y) // 递归 向上探索
dfs(grid, x, y-1) // 递归 向左探索
}
|
BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
func numIslands(grid [][]byte) int {
res := 0
for i := range grid {
for j := range grid[i] {
if grid[i][j] == '1' { // 遇到陆地节点且没有被标记过
res += 1
bfs(grid, i, j)
}
}
}
return res
}
func bfs(grid [][]byte, x int, y int) {
queue := make([][]int, 0) // 定义队列
queue = append(queue, []int{x, y}) // 起始节点入队
move := [4][2]int{{1, 0}, {0, 1}, {0, -1}, {-1, 0}} // 下右左上
for len(queue) != 0 { // 遍历队列
node := queue[0] // 取队首元素
queue = queue[1:] // 更新队列
for i := 0; i < 4; i++ { // 遍历当前节点四周
x = node[0] + move[i][0]
y = node[1] + move[i][1]
// 下标越界或遇到海洋节点
if x < 0 || y < 0 || x == len(grid) || y == len(grid[x]) || grid[x][y] == '0' {
continue
}
grid[x][y] = '0' // 标记节点
queue = append(queue, []int{x, y}) // 入队
}
}
}
|
岛屿的最大面积
695. 岛屿的最大面积 - 力扣(LeetCode)
给定一个二维数组,表示一块区域;元素由0和1组成,1代表陆地,0代表海洋;若陆地被海洋包裹,则说明是岛屿;假设该区域四条边外是海洋;被海洋包裹的多块水平或垂直相连陆地看作一个岛屿;返回该区域中岛屿的最大面积
本题思路:遍历一遍所有节点;每遇到一个陆地节点且没有被标记过,说明是新岛屿,然后把该陆地节点所能遍历到的陆地都标记上;在遇到标记过的陆地节点和海洋节点的时候直接跳过;在标记时统计该岛屿的面积,遍历该岛屿结束后,与已保存的最大岛屿面积作比较取最大值,
把陆地节点所能遍历到的陆地都标记上可以使用 DFS,BFS或者并查集
对于本题来说,DFS和BFS都是对一个节点进行四周遍历,区别是DFS用递归栈来保存遍历过的状态,BFS用队列来保存遍历过的状态
DFS
- 递归参数:一个是图用来遍历,一个是目前遍历的节点的横纵坐标(坐标用来访问四周节点),记录每个岛屿面积的变量可设为全局
- 确认终止条件:索引越界或遇到海洋
- 处理目前搜索节点出发的路径:得到当前遍历节点的指向的下一个节点
注意:每次遍历完岛屿并记录结束后,要清空全局变量,使其在下次岛屿遍历中记录
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
var area int
func maxAreaOfIsland(grid [][]int) int {
res := 0
for i := range grid {
for j := range grid[i] {
if grid[i][j] == 1 {
dfs(grid, i, j)
res = max(res, area)
area = 0 // 重置面积
}
}
}
return res
}
func dfs(grid [][]int, x int, y int) {
if x < 0 || y < 0 || x == len(grid) || y == len(grid[x]) || grid[x][y] == 0 {
return
}
grid[x][y] = 0 // 标记
area += 1 // 统计面积
dfs(grid, x+1, y) // 下
dfs(grid, x, y+1) // 右
dfs(grid, x-1, y) // 上
dfs(grid, x, y-1) // 左
}
|
飞地的数量
1020. 飞地的数量 - 力扣(LeetCode)
给定一个二维数组,表示一块区域;元素由0和1组成,1代表陆地,0代表海洋;若陆地被海洋包裹,则说明是岛屿;假设该区域四条边外是海洋;被海洋包裹的多块水平或垂直相连陆地看作一个岛屿;返回该区域中所有不能到达矩阵边界的岛屿的面积总和
本题思路一:遍历一遍所有节点;每遇到一个陆地节点且没有被标记过,说明是新岛屿,然后把该陆地节点所能遍历到的陆地都标记上;在遇到标记过的陆地节点和海洋节点的时候直接跳过;在标记时统计该岛屿的面积,同时检查该节点是否到达边界,一旦该岛屿可以到达边界则标记该岛屿;遍历该岛屿结束后,若该岛屿不能到达边界,则将该岛屿面积记入结果集
思路二:本题要求找到不靠边的陆地面积,那么我们只要从周边找到陆地然后 通过 dfs或者bfs 将周边靠陆地且相邻的陆地都变成海洋,然后再去重新遍历地图的时候,统计此时还剩下的陆地就可以了。
把陆地节点所能遍历到的陆地都标记上可以使用 DFS,BFS或者并查集
对于本题来说,DFS和BFS都是对一个节点进行四周遍历,区别是DFS用递归栈来保存遍历过的状态,BFS用队列来保存遍历过的状态
思路一DFS
- 递归参数:一个是图用来遍历,一个是目前遍历的节点的横纵坐标(坐标用来访问四周节点),记录每个岛屿面积的变量和标记该岛屿能否到达矩阵边界的变量可设为全局
- 确认终止条件:索引越界或遇到海洋
- 处理目前搜索节点出发的路径:得到当前遍历节点的指向的下一个节点
注意:每次遍历完岛屿并记录结束后,要清空全局变量,使其在下次岛屿遍历中记录
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
var area int
var arrived bool
func numEnclaves(grid [][]int) int {
res := 0
for i := range grid {
for j := range grid[i] {
if grid[i][j] == 1 {
dfs(grid, i, j)
if !arrived {
res += area // 记录不能到达边界的面积
}
area = 0 // 重置
arrived = false // 重置
}
}
}
return res
}
func dfs(grid [][]int, x int, y int) {
if x < 0 || y < 0 || x == len(grid) || y == len(grid[x]) {
arrived = true // 上一块陆地是边界
return
}
if grid[x][y] == 0 {
return
}
grid[x][y] = 0 // 标记
area += 1 // 统计面积
dfs(grid, x+1, y) // 下
dfs(grid, x, y+1) // 右
dfs(grid, x-1, y) // 上
dfs(grid, x, y-1) // 左
}
|
被围绕的区域
130. 被围绕的区域 - 力扣(LeetCode)
给定一个二维数组,表示一块区域;元素由x和o组成,o代表陆地,x代表海洋;若陆地被海洋包裹,则说明是岛屿;假设该区域四条边外是海洋;被海洋包裹的多块水平或垂直相连陆地看作一个岛屿;将该区域中所有不能到达矩阵边界的岛屿的都置为海洋
本题思路:遍历一遍所有节点;每遇到一个陆地节点且没有被标记过,说明是新岛屿,然后把该陆地节点所能遍历到的陆地都标记上;在遇到标记过的陆地节点和海洋节点的时候直接跳过;在标记时检查该节点是否到达边界,一旦该岛屿可以到达边界则标记该岛屿;遍历岛屿结束后,若该岛屿不能到达边界则将其陆地置为海洋;遍历区域结束后,若不能到达边界的岛屿置为海洋
思路二:遍历地图周边一圈,将周边空格相邻的’O’都做上标记,然后再遍历一遍地图,遇到 ‘O’ 且没做过标记的,那么都是地图中间的’O',全部改成’X’就行。
把陆地节点所能遍历到的陆地都标记上可以使用 DFS,BFS或者并查集
对于本题来说,DFS和BFS都是对一个节点进行四周遍历,区别是DFS用递归栈来保存遍历过的状态,BFS用队列来保存遍历过的状态
思路二DFS
- 递归参数:一个是图用来遍历,一个是目前遍历的节点的横纵坐标(坐标用来访问四周节点),记录标记过的陆地的变量可设为全局
- 确认终止条件:索引越界或遇到海洋
- 处理目前搜索节点出发的路径:得到当前遍历节点的指向的下一个节点
注意:标记可到边界的陆地可直接将该陆地置为其他值,后面遍历区域时再将其恢复;用此方法时注意最后遍历时要用if elseif;用此方法时注意DFS中遇到标记过的变量也要返回,不然会死循环一直标记标记过的变量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
func solve(board [][]byte) {
for row := 0; row < len(board); row++ {
if board[row][0] == 'O' { // 第一列
dfs(board, row, 0)
}
if board[row][len(board[0])-1] == 'O' { // 最后一列
dfs(board, row, len(board[0])-1)
}
}
for col := 1; col < len(board[0])-1; col++ {
if board[0][col] == 'O' { // 第一排去首尾剩下中间的
dfs(board, 0, col)
}
if board[len(board)-1][col] == 'O' { // 最后一排去首尾剩下中间的
dfs(board, len(board)-1, col)
}
}
for i := range board {
for j := range board[i] {
if board[i][j] == 'A' {
board[i][j] = 'O' // 恢复可以到达边界的陆地
} else if board[i][j] == 'O' {
board[i][j] = 'X' // 不能到达边界的陆地
}
}
}
}
func dfs(board [][]byte, x int, y int) {
if x < 0 || y < 0 || x == len(board) || y == len(board[x]) || board[x][y] == 'X' || board[x][y] == 'A' {
return
}
board[x][y] = 'A' // 标记该陆地
dfs(board, x+1, y) // 下
dfs(board, x, y+1) // 右
dfs(board, x-1, y) // 上
dfs(board, x, y-1) // 左
}
|
太平洋大西洋水流问题
417. 太平洋大西洋水流问题 - 力扣(LeetCode)
给定一个二维数组,表示一块岛屿,该岛屿左方和上方被太平洋包围,右方和下方被大西洋包围;每个元素表示每块陆地的高度,水可以从高流向相等或小于的陆地;水到岛屿边缘就可以直接入海;返回可以同时流入大西洋和太平洋的陆地坐标
反过来想,从太平洋边上的节点 逆流而上,将遍历过的节点都标记上;从大西洋的边上节点 逆流而上,将遍历过的节点也标记上; 最后遍历岛屿,两方都标记过的节点就是既可以流到太平洋也可以流到大西洋的陆地
用一个三维数组来标记节点,前两个维度标记节点横纵坐标,第三个维度长度为2标记节点能否到达太平洋好大西洋,可作为全局变量;dfs时第三维作为入参标记当前从哪个洋逆流而上
dfs遍历时,需要当前节点和前一个节点的状态比较,可以先比较再决定是否递归遍历,这就需要四个偏移量来计算向四周移动后的坐标,遍历四个偏移量来表示向四周遍历
DFS
注意:
- 先遍历第一列太平洋和最后一列大西洋后,再次遍历排时仍要从当前排第一个元素出发,因为副对角俩元素可以同时到达两个洋
- 由于是在循环中遍历四个方向所以是跳过本次循环,不是
return返回
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
var visited [][][]bool
var ds = [4][2]int{{1, 0}, {0, 1}, {-1, 0}, {0, -1}} // 四周偏移量
func pacificAtlantic(heights [][]int) [][]int {
res := make([][]int, 0)
visited = make([][][]bool, len(heights))
for i := range visited {
visited[i] = make([][]bool, len(heights[i]))
}
for i := range visited {
for j := range visited[i] {
visited[i][j] = make([]bool, 2)
}
}
for row := 0; row < len(heights); row++ {
dfs(heights, row, 0, 0) // 标记第一列太平洋
dfs(heights, row, len(heights[0])-1, 1) // 标记最后一列大西洋
}
for col := 0; col < len(heights[0]); col++ {
dfs(heights, 0, col, 0) // 标记第一排太平洋
dfs(heights, len(heights)-1, col, 1) // 标记最后一排大西洋
}
for i := range heights {
for j := range heights[i] {
if visited[i][j][0] && visited[i][j][1] {
res = append(res, []int{i, j})
}
}
}
return res
}
func dfs(heights [][]int, x int, y int, sign int) {
visited[x][y][sign] = true
for _, move := range ds {
curX := x + move[0]
curY := y + move[1]
if curX < 0 || curY < 0 || curX == len(heights) || curY == len(heights[curX]) {
continue // 索引越界
}
if heights[x][y] > heights[curX][curY] || visited[curX][curY][sign] {
continue // 高度不合适或标记过
}
dfs(heights, curX, curY, sign)
}
}
|
最大人工岛
827. 最大人工岛 - 力扣(LeetCode)
给定一个二维数组,表示一块区域;元素由0和1组成,1代表陆地,0代表海洋;若陆地被海洋包裹,则说明是岛屿;假设该区域四条边外是海洋;被海洋包裹的多块水平或垂直相连陆地看作一个岛屿;现在可以改变一个海洋使其变为陆地,返回改变后的最大岛屿面积
思路:
- 遍历地图一次,得出各个岛屿的面积,并做编号记录,可以使用map记录,key为岛屿编号,value为岛屿面积
- 再遍历地图一次,遇到0就统计其四周相邻岛屿的面积(用到上一步记录好的岛屿面积),将面积加在一起后再加一得到一个总面积,记录后恢复该1为0继续向后遍历,遍历所有 0 之后,就可以得出 选一个0变成1 之后的最大面积
优化:第一次遍历时可以直接修改原数组的元素值作为标记,在遍历完一个岛屿后统计其面积,并将标记值加一
注意:
- 第二次遍历统计0四周岛屿面积时需要再用一个map记录该岛屿是否被统计过,因为有的岛屿可能占用0四周的多个陆地
- 最后返回结果需要判断是否改变过0,若没有,说明该区域全是陆地,直接返回区域中陆地数
- for循环遍历四周时需要用新变量来表示四周坐标,不能直接修改原坐标,因为递归返回上一层时需要用到本层的坐标
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
var ds = [4][2]int{{1, 0}, {0, 1}, {-1, 0}, {0, -1}}
var mark int
var area int
func largestIsland(grid [][]int) int {
res := 0
mark = 2
getSize := make(map[int]int)
// 统计各个岛屿面积
for i := range grid {
for j := range grid[i] {
if grid[i][j] == 1 {
dfs(grid, i, j) // 遍历该岛屿
getSize[mark] = area // 保存岛屿面积
area = 0 // 置零
mark++ // 标记值更新
}
}
}
// 遍历0得到最大面积
for i := range grid {
for j := range grid[i] {
if grid[i][j] == 0 {
// 得到四周岛屿总面积
total := 0
accounted := make(map[int]bool)
for _, move := range ds {
x := i + move[0]
y := j + move[1]
if x < 0 || y < 0 || x == len(grid) || y == len(grid[x]) || grid[x][y] == 0 {
continue // 索引越界或遇到海洋
} else if accounted[grid[x][y]] {
continue // 该岛屿被统计过
} else {
accounted[grid[x][y]] = true // 标记该岛屿
total += getSize[grid[x][y]] // 统计该岛屿面积
}
}
res = max(res, 1+total) // 更新最大面积
}
}
}
if res == 0 {
return len(grid) * len(grid)
}
return res
}
func dfs(grid [][]int, x int, y int) {
if x < 0 || y < 0 || x == len(grid) || y == len(grid[x]) || grid[x][y] != 1 {
return // 索引越界或遇到海洋或标记过
}
grid[x][y] = mark // 标记陆地
area++ // 岛屿面积更新
for _, move := range ds {
curX := x + move[0]
curY := y + move[1]
dfs(grid, curX, curY)
}
}
|
单词接龙
127. 单词接龙 - 力扣(LeetCode)
给定两个单词 beginWord 、 endWord 和一个字典 wordList ;每次从字典中选一个单词,该单词和上一个单词只有一个字母不同,返回 从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 ;序列中第一个单词是 beginWord,序列中最后一个单词是 endWord;beginWord不在字典中,endWord在字典中;如果不存在这样的转换序列,返回 0
以示例1为例,从这个图中可以看出 hit 到 cog 的路线,不止一条,有三条,一条是最短的长度为5,两条长度为6
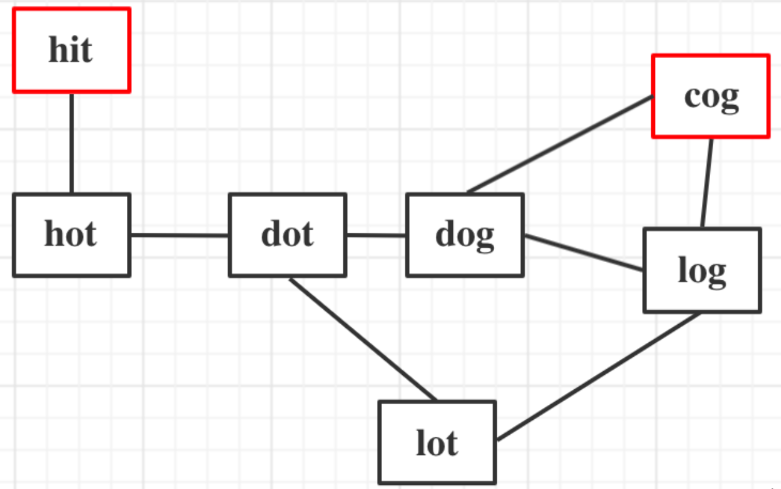
本题要解决两个问题:
- 怎样表示图中的链接:若俩单词只有一个字符不同,则有链接
- 起点和终点的最短路径长度:无向图求最短路,广搜最为合适;广搜只要搜到了终点,则一定是最短的路径,因为广搜就是以起点中心向四周扩散的搜索;本题如果用深搜会比较麻烦,要在到达终点的不同路径中选则一条最短路, 而广搜只要达到终点,一定是最短路
优化:字典可以转成map结构,查找更快一些
注意:
- 无向图需要标记节点是否走过,否则会死循环;本题即标记该单词是否用过
- 比较俩单词是否只差一个单词时,对单词中每个字母用26个字母逐个替换并检索字典中是否存在,若存在则路径长度加一,若为最终单词则返回,否则更新路径长度后入队
- go中字符串和字符互相转换:
[]rune(s)、string([]rune) ,只处理英文用byte,遍历26字母时go中用的是rune
- 遍历下一个字符前需要将上一个字符的状态复原
- 对每个单词记录其路径长度,同时作为是否访问过的标志,由于是BFS所以找到一个链接后,还会继续找本单词的其他链接,所以不能用一个变量来记录路径长度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
func ladderLength(beginWord string, endWord string, wordList []string) int {
// 转换字典为map型
wordMap := make(map[string]int)
for i, v := range wordList {
wordMap[v] = i
}
// BFS
length := make(map[string]int)
length[beginWord] = 1
queue := make([]string, 0) // 定义队列
queue = append(queue, beginWord) // 入队
for len(queue) != 0 {
word := queue[0] // 取队头元素
path := length[word] // 获取该单词的路径长度
queue = queue[1:] // 队首出队
for i := range word {
wordSlice := []rune(word) // 将单词转为字符数组
for k := 'a'; k <= 'z'; k++ {
wordSlice[i] = k // 替换字符
if _, ok := wordMap[string(wordSlice)]; ok { // 在字典中
if _, ok := length[string(wordSlice)]; !ok { // 未被使用过
length[string(wordSlice)] = path + 1 // 记录单词对应的路径长度
if string(wordSlice) == endWord {
return length[string(wordSlice)] // 到最终单词
}
queue = append(queue, string(wordSlice)) // 入队
}
}
}
}
}
return 0
}
|
钥匙和房间
841. 钥匙和房间 - 力扣(LeetCode)
给定一个二维数组,第一维表示房间,第二维表示房间中的钥匙;0号房间一定是打开的,进入房间必须要钥匙,可以通过进入房间获得其他房间的钥匙;若能够进入所有房间则返回true,否则返回false
用一个数组记录所有房间的可否进入状态,同时也作为是否入过队的标志;BFS遍历给定二维数组,获得新钥匙就更新房间的可进入状态;最后遍历所有房间的可进入状态
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
func canVisitAllRooms(rooms [][]int) bool {
accessible := make([]bool, len(rooms))
accessible[0] = true // 0号房间可进入
queue := make([][]int, 0) // 定义队列
queue = append(queue, rooms[0]) // 0号房入队
for len(queue) != 0 {
room := queue[0] // 取队首
queue = queue[1:] // 出队
for _, key := range room { // 遍历本房间中钥匙
if !accessible[key] { // 此房间未入过队
accessible[key] = true // 更新可进入状态
queue = append(queue, rooms[key]) // 新房入队
}
}
}
for i := range accessible {
if !accessible[i] {
return false // 有房间无法进入
}
}
return true
}
|
BFS优化:队列用一维数组保存房间下标
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
func canVisitAllRooms(rooms [][]int) bool {
accessible := make([]bool, len(rooms))
accessible[0] = true // 0号房间可进入
queue := make([]int, 0) // 定义队列
queue = append(queue, 0) // 0号房入队
for len(queue) != 0 {
idx := queue[0] // 取队首
queue = queue[1:] // 出队
for _, key := range rooms[idx] { // 遍历本房间中钥匙
if !accessible[key] { // 此房间未入过队
accessible[key] = true // 更新可进入状态
queue = append(queue, key) // 新房入队
}
}
}
for i := range accessible {
if !accessible[i] {
return false // 有房间无法进入
}
}
return true
}
|
岛屿的周长
463. 岛屿的周长 - 力扣(LeetCode)
给定一个二维数组,表示一块区域;元素由0和1组成,1代表陆地,0代表海洋;若陆地被海洋包裹,则说明是岛屿;假设该区域四条边外是海洋;被海洋包裹的多块水平或垂直相连陆地看作一个岛屿;该区域中恰好有一个岛屿,求该岛屿的周长
遍历区域,每遇到一个陆地,岛屿周长就加四;查看该陆地的四周,每有一个岛屿,则周长减一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
func islandPerimeter(grid [][]int) int {
res := 0
for i := range grid {
for j := range grid[i] {
if grid[i][j] == 1 { // 遇到陆地
res += 4
if j != len(grid[0])-1 && grid[i][j+1] == 1 {res -= 1} // 不是最后一列且右有陆地
if i != len(grid)-1 && grid[i+1][j] == 1 {res -= 1} // 不是最后一排且下有陆地
if i != 0 && grid[i-1][j] == 1 {res -= 1} // 不是第一排且上有陆地
if j != 0 && grid[i][j-1] == 1 {res -= 1} // 不是第一列且左有陆地
}
}
}
return res
}
|
寻找图中是否存在路径
1971. 寻找图中是否存在路径 - 力扣(LeetCode)
给定整数 n表示节点总数、二维数组 edges 表示边、source 和 destination表示起点和终点,如果从 source 到 destination 存在 有效路径 ,则返回 true,否则返回 false
本题判断起点和终点是否连通,也就是判断是否在一个集合里,可以用并查集来判断
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
var father []int
func validPath(n int, edges [][]int, source int, destination int) bool {
father = make([]int, n)
initial(n)
for i := range edges {
join(edges[i][0], edges[i][1])
}
return isSame(source, destination)
}
// 并查集初始化
func initial(n int) {
for i := 0; i < n; i++ {
father[i] = i
}
}
// 并查集里寻根
func find(u int) int {
if father[u] == u {
return u
}
father[u] = find(father[u])
return father[u]
}
// 判断a和b是否找到同一个根
func isSame(a int, b int) bool {
a = find(a)
b = find(b)
return a == b
}
// 边a->b加入并差集
func join(a int, b int) {
a = find(a)
b = find(b)
if a == b {
return // 同根说明已经在一个集合里
}
father[a] = b
}
|
冗余连接
684. 冗余连接 - 力扣(LeetCode)
给定一个二维数组表示图中的边;要求去掉一条边,使图变为树(只有一个根节点);返回该边,若有多个答案,返回二维数组中的最后一条边
遍历给定边,在将边加入并查集的过程中,若发现边的俩节点同根,说明该边加入后一定会形成环,返回该边即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
var father []int
var n int
func findRedundantConnection(edges [][]int) []int {
n = len(edges)
father = make([]int, n+1)
initial()
for i := 0; i < n; i++ {
if isSame(edges[i][0], edges[i][1]) {
return edges[i]
}
join(edges[i][0], edges[i][1])
}
return []int{}
}
func initial() {
for i := 0; i <= n; i++ {
father[i] = i
}
}
func isSame(a int, b int) bool {
a = find(a)
b = find(b)
return a == b
}
func find(u int) int {
if father[u] == u {
return u
}
father[u] = find(father[u])
return father[u]
}
func join(a int, b int) {
a = find(a)
b = find(b)
if a == b {
return
}
father[a] = b
}
|
冗余连接 II
685. 冗余连接 II - 力扣(LeetCode)
给定一个二维数组表示图中的有向边;要求去掉一条边(只有一个根节点),使图变为树;返回该边,若有多个答案,返回二维数组中的最后一条边
由于是有向边,所以需要考虑到边的方向,可以将删除边的情况分为两种,一种是有入度为2的节点,另一种是没有入度为2的节点
- 若有入度为2的节点,则需要在两条边中选择一条删除,且删除二维数组中后面的那一条
- 若无入度为2的节点,则说明仅存在一个有向环,这时和上一题一样只需要找出加入一条边,一旦该边加入即成环,返回该边即可
思路:
- 第一遍遍历各个边,统计每个节点的入度,节点值作为索引,度数作为值
- 第二遍遍历各个边,一旦发现该边指向的节点入度为2,则将该边记录;若有入度为2的节点,一定会统计出两条边
- 若第二遍遍历中能统计到两条边,则先看删掉第二条边(数组中靠后)后能否构成树,若可以则返回该边,否则返回第一条边
- 初始化并查集;将各个边加入并查集;在加入前判断,若要加入的边是要删除的边则不加入,若要加入的边加入后会成环则说明不能成树返回
false
- 若第二遍遍历中没有统计到两条边,说明只存在一个有向环,则找到构成环的边返回即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
|
var father []int
var n int
func findRedundantDirectedConnection(edges [][]int) []int {
inDegree := make([]int, len(edges)+1) // 记录各节点的入度
for i := range edges {
inDegree[edges[i][1]] += 1
}
twoDegree := make([]int, 0) // 记录入度为2的节点的两条边的索引
for i := range edges {
if inDegree[edges[i][1]] == 2 {
twoDegree = append(twoDegree, i) // 找到入度为2的节点的一条边
}
}
if len(twoDegree) != 0 {
if isTreeAfterRemoveEdge(edges, twoDegree[1]) {
return edges[twoDegree[1]] // 去掉数组中靠后的该边能构成树
}
return edges[twoDegree[0]] // 去掉数组中靠前的该边能构成树
}
return getRemoveEdge(edges)
}
// isTreeAfterRemoveEdge 判断删除一条边之后能否成树
func isTreeAfterRemoveEdge(edges [][]int, deleteEdgeIdx int) bool {
n = len(edges)
father = make([]int, n+1)
initial()
for i := range edges {
if i == deleteEdgeIdx {
continue // 不添加要删除的边
}
if isSame(edges[i][0], edges[i][1]) {
return false // 该边加入会成环说明不能成树
}
join(edges[i][0], edges[i][1]) // 加入并查集
}
return true
}
// getRemoveEdge 找到加入后会成环的边
func getRemoveEdge(edges [][]int) []int {
n = len(edges)
father = make([]int, n+1)
initial()
for i := range edges {
if isSame(edges[i][0], edges[i][1]) {
return edges[i] // 找到加入后会成环的边
}
join(edges[i][0], edges[i][1]) // 加入并查集
}
return []int{}
}
// 并查集
func initial() {
for i := 0; i <= n; i++ {
father[i] = i
}
}
func isSame(a int, b int) bool {
a = find(a)
b = find(b)
return a == b
}
func find(u int) int {
if father[u] == u {
return u
}
father[u] = find(father[u])
return father[u]
}
func join(a int, b int) {
a = find(a)
b = find(b)
if a == b {
return
}
father[a] = b
}
|